
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение линейного корреляционного уравненияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим практический подход к построению линейного корреляционного уравнения (уравнения регрессии). При большом числе наблюдений одно и то же значение х может встретиться nx раз, одно и то же значение у - nу раз, одна и та же пара чисел (х, у) может наблюдаться nху раз. Поэтому данные наблюдений группируют, то есть подсчитывают частоты nх, nу, nху. Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной. Поясним устройство корреляционной таблицы на примере.
В первой строке таблицы указаны наблюдаемые значения (10, 20, 30, 40) признака Х, а в первом столбце - наблюдаемые значения (0,4; 0,6; 0,8) признака Y. На пересечении строк и столбцов находятся частоты nxy наблюдаемых пар значений признаков. Например, частота 5 указывает, что пара чисел (10; 0,4) наблюдалась 5 раз. (Все частоты выделены жирным шрифтом. Прочерк означает, что соответствующая пара чисел, например (20; 0,4), не наблюдалась). В последнем столбце записаны суммы частот строк. Например, сумма частот первой строки широкого прямоугольника равна nу = 5 + 7 + 14 = 26; это число указывает, что значение признака Y, равное 0,4 (в сочетании с различными значениями Х), наблюдалось 26 раз. В клетке, расположенной в нижнем правом углу таблицы, помещена сумма всех частот (общее число всех наблюдений n). Очевидно
Так как практически для удовлетворительной оценки искомых параметров должно быть проведено достаточно большое число наблюдений, причём среди полученных данных есть повторяющиеся, и они сгруппированы в виде корреляционной таблицы, то целесообразно, введя новую величину - выборочный коэффициент корреляции rв, написать уравнение прямой линии регрессии Y на Х (5) в виде
где
где sх, sу - выборочные средние квадратические отклонения; х, у - варианты (наблюдаемые значения) признаков X и Y; nху - частота пары вариант (х, у); n - объем выборки (сумма всех частот). Условным средним Выборочный коэффициент корреляции rВ является оценкой коэффициента корреляции r генеральной совокупности и поэтому также служит для измерения линейной связи между величинами - количественными признаками Y и Х. Если выборка имеет достаточно большой объем и хорошо представляет генеральную совокупность (репрезентативна), то заключение о тесноте линейной зависимости между признаками, полученное по данным выборки, в известной степени может быть распространено и на генеральную совокупность. Если данные наблюдений над признаками Х и Y заданы в виде корреляционной таблицы с равноотстоящими вариантами (h - const), то целесообразно перейти к условным вариантам
где С1 - ложный нуль вариант Х (новое начало отсчета), в качестве которой выгодно принять варианту, расположенную примерно в середине вариационного ряда (обычно в качестве ложного нуля принимают варианту, имеющую наибольшую частоту); h1 - шаг, то есть разность между двумя соседними вариантами Х; С2 - ложный нуль вариант Y; h2 - шаг вариант Y. Формула для вычисления коэффициента корреляции принимает вид
причем, для вычисления слагаемого Величины
Зная эти величины, можно определить входящие в уравнение регрессии параметры по формулам
Пример. Найти выборочное уравнение прямой линии
регрессии Y на Х по данным корреляционной таблицы.
Решение. Составим корреляционную таблицу в условных вариантах, выбрав в качестве ложных нулей С1 = 30, С2 = 36. Найдем
Найдем вспомогательные величины
Найдем su и sv
Найдем Дадим некоторые пояснения к составлению расчетной таблицы. 1. Произведение частоты nuv на варианту u, то есть nuv×u записывают в правом верхнем углу клетки, содержащей значение частоты. Например, в правых верхних углах клеток первой строки записаны произведения: 4×(-2) = -8; 6×(-1) = -6. 2. Складывают все числа, помещенные в правых верхних углах клеток одной строки, и их сумму помещают в клетку этой же строки «столбца U». Например, для первой строки
3. Наконец, умножают варианту v на U и полученное произведение записывают в соответствующую клетку «столбца v×U». Например, в первой строке таблицы v = -2; U = -14; следовательно,
4. Сложив все числа «столбца v×U», получают сумму Для контроля аналогичные вычисления производят по столбцам: - произведения nuv×v записывают в левый нижний угол клетки, содержащей значение частоты; - все числа, помещенные в левых нижних углах одного столбца, складывают и их сумму помещают в «строку V»; - наконец, умножают каждую варианту u на V и результаты записывают в клетках последней строки. Сложив все числа последней строки, получают сумму Например, Найдем искомый выборочный коэффициент корреляции
Найдем шаги h1 и h2 (разность между любыми двумя соседними вариантами)
Найдем
Найдем sх и sу
Подставив найденные величины в соотношение (*), получим искомое уравнение прямой линии регрессии Y на Х
или окончательно
Контрольные задания
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1060; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

 .
. 0,
0,  .
.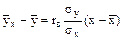 ,
,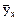 - условная средняя,
- условная средняя, 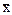 и
и  - выборочные средние признаков X и Y, rв - выборочный коэффициент корреляции, причём
- выборочные средние признаков X и Y, rв - выборочный коэффициент корреляции, причём ,
,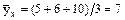 .
.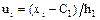 ,
, 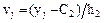 ,
,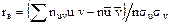 ,
,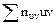 удобно составить расчетную таблицу (см. ниже).
удобно составить расчетную таблицу (см. ниже). могут быть вычислены либо рассмотренным выше методом произведений (при большом числе данных), либо непосредственно по формулам.
могут быть вычислены либо рассмотренным выше методом произведений (при большом числе данных), либо непосредственно по формулам.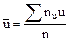 ,
,  ,
, 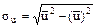 ,
, 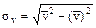 .
. ,
, 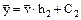 ,
, 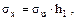
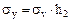 .
.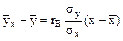 (*)
(*)
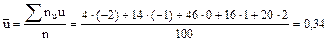 ;
; .
.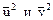
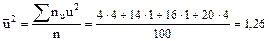 ,
, .
. ,
, .
. , для чего составим расчетную таблицу (см. ниже).
, для чего составим расчетную таблицу (см. ниже).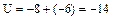 .
.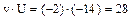 .
. контроль
контроль
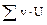 , которая равна искомой сумме
, которая равна искомой сумме 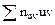 . Например,
. Например,  , следовательно, искомая сумма
, следовательно, искомая сумма 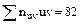 .
.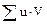 , которая также равна искомой сумме
, которая также равна искомой сумме 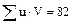 , следовательно,
, следовательно, 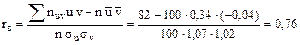 .
.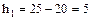 ;
; 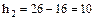 .
. , учитывая, что С1 = 30, С2 = 36,
, учитывая, что С1 = 30, С2 = 36, ;
;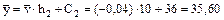 .
.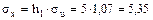 ;
; .
.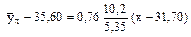 ,
, .
.


