
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подчеркнем, что порядок событий безразличен.Содержание книги
Поиск на нашем сайте Пример 1. В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобраны 3 человека. Найти вероятность того, что все отобранные лица окажутся мужчинами. Решение. Вероятность того, что первым будет отобран мужчина (событие А) равна Р(А) = Вероятность того, что вторым отобран мужчина (событие В), при условии, что первым уже был отобран мужчина, то есть условная вероятность события В равна
Вероятность того, что третьим будет отобран мужчина, при условии, что уже отобраны двое мужчин, то есть условная вероятность события С РАВ(С) = Искомая вероятность
Определение. Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, то есть если условная вероятность события В равна его безусловной вероятности
Из (12), с учетом (*), следует РВ(А) = Р(А). (**) Итак, если событие В не зависит от события А, то и событие А не зависит от события В. Иными словами, свойство независимости и зависимости взаимно. Для независимых событий (11) принимает вид Р(АВ) = Р(А) × Р(В). (***) Равенство (***) может служить определением независимых событий, то есть два события А и В называются независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми. События А1, А2, А3, …, Аn называются попарно независимыми, если любые два из них независимы между собой. События А1, А2, А3, …, Аn называются независимыми в совокупности, если вероятность каждого из них не меняется при наступлении других событий (одного или нескольких в любой комбинации и в любом числе). Независимость событий в совокупности является более сильным требованием, чем их попарная независимость. Вероятность произведения конечного числа независимых в совокупности событий равна произведению их вероятностей, то есть формула (13) принимает вид Р(А1 А2 … Аn) = Р(А1) × Р(А2) … Р(Аn). (14) Заметим, что если события А1, А2, …, Аn независимы в совокупности, то и противоположные события Теорема. Вероятность появления хотя бы одного из событий А1, А2, …, Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий Р(А) = 1 – q1q2 … qn. (15)
Доказательство. Если А, событие состоящее в появлении хотя бы одного из событий А1, А2, …, Аn, то события А и Р(А) + Р( или Р(А) = 1 – Р(
Пользуясь теоремой умножения, получим
Р(А) = 1 - Если
тогда (15) примет вид Р(А) = 1 -
Следствия теорем сложения и умножения
Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления Р(А + В) = Р(А) + Р(В) - Р(АВ). (17) При использовании формулы (17) следует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми. Для независимых событий Р(А + В) = Р(А) + Р(В) - Р(А) × Р(В). Для зависимых событий Р(А + В) = Р(А) + Р(В) - Р(А) × РА(В). Если события А и В несовместны, то Р(АВ) = 0 и (17) примет вид Р(А + В) = Р(А) + Р(В). Таким образом, формула (17) справедлива как для совместных, так и для несовместных событий.
Пример 2. Три стрелка стреляют по цели. Вероятность попадания в цель первым стрелком равна 0,75, вторым стрелком - 0,8, третьим стрелком - 0,9. Определить вероятность того, что все три стрелка одновременно попадут в цель. Решение. Р(А) = 0,75, Р(В) = 0,8, Р(С) = 0,9. Р(АВС) = Р(А) × Р(В) × Р(С) = 0,75 × 0,8 × 0,9 = 0,54. Пример 3. Вероятности появления каждого их трех независимых событий А1, А2, А3 соответственно равны р1, р2, р3. Найти вероятность появления только одного из этих событий. Решение. Заметим, что, например, появление только первого события А1 равносильно появлению события В1 - появилось только событие А1, то есть В1 = В2 - появилось только событие А2, то есть В2 = В3 - появилось только событие А3, то есть В3 = Таким образом, надо найти вероятность события В1 + В2 + В3, то есть вероятность появления одного, безразлично какого, из событий В1, В2, В3. Так как события В1, В2, В3 несовместны, то применима теорема сложения Р(В1 + В2 + В3) = Р(В1) + Р(В2) + Р(В3). (*)
Остается найти вероятности каждого из событий В1, В2, В3. События А1, А2, А3 независимы, следовательно, независимы события Р(В1) = Р ( Аналогично Р(В2) = Р(
Р(В3) = Р(
Подставив эти вероятности в (*), найдём искомую вероятность
Р(В1 + В2 + В3) = р1q1q3 + q1p2q3 + q1q2p3.
Пример 4. Вероятности попадания в цель при стрельбе из трех орудий таковы: р1 = 0,8, р2 = 0,7, р3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий. Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события А1 (попадание первого орудия), А2 (попадание второго орудия) и А3 (попадание третьего орудия) независимы в совокупности. Вероятности событий, противоположных событиям А1, А2 и А3 (то есть вероятности промахов), соответственно равны
q1 = 1 - p1 = 0,2, q2 = 1 - p2 = 0,3, q3 = 1 - p3 = 0,1.
Искомая вероятность Р(А) = 1 - q1q2q3 = 1 - 0,2 × 0,3 × 0,1 = 0,994.
Пример 5. Вероятность того, что событие появится хотя бы один раз в трех независимых в совокупности испытаниях, равна 0,936. Найти вероятность появления события в одном испытании, (вероятность появления события в одном испытании постоянна). Решение. Так как рассматриваемые события независимы в совокупности, то применима формула (16) Р(А) = 1 -
По условию, Р(А) = 0,936; n = 3. Следовательно,
0,936 = 1 - q3 или q3 = 1 - 0,936 = 0,064.
Отсюда q = Искомая вероятность p = 1 - q = 1 - 0,4 = 0,6.
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.009 с.) |

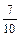 .
.
 .
.
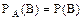 . (*)
. (*) также независимы в совокупности.
также независимы в совокупности. ) = 1
) = 1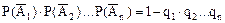 .
.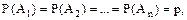 то
то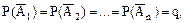
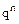 . (16)
. (16)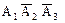 (появилось первое и не появились второе и третье события). Введем обозначения:
(появилось первое и не появились второе и третье события). Введем обозначения: ;
; ;
; .
.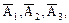 поэтому применима теорема умножения
поэтому применима теорема умножения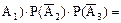 р1q2q3.
р1q2q3. q1p2q3;
q1p2q3;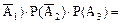 q1q2p3.
q1q2p3.



