Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальное распределение в приложенияхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нормальное распределение или распределение Гаусса является наиболее распространенным в природе законом распределения случайных величин. Это распределение имеет место в том случае, если случайная величина зависит от большого числа факторов, могущих вносить с равной вероятностью положительные и отрицательные отклонения. Нормальная кривая обладает следующими особенностями. Она похожа на колокол (рис. 11). Спадает одинаково в обе стороны сначала медленно, а потом быстро. Математику достаточно знать три параметра, чтобы построить эту кривую, а именно: высоту её максимума, среднее значение изучаемой величины (это и есть то место на горизонтальной оси х = а, которое соответствует горбу кривой) и ширину кривой. Условно её мерят на полувысоте колокола. Очевидно, что ширина показывает, насколько часто или редко встречается отклонение от среднего. Чем уже колокол, тем менее часты значительные отклонения от среднего. На рис. 12 представлена кривая распределения роста женщин [8], которая подчиняется нормальному закону. Она описывается так. Высота кривой 225 человек, т.е. двести двадцать пять человек имеют средний рост (первый параметр кривой). Заметим, что иметь средний рост в буквальном смысле слова невозможно, можно иметь средний рост с точностью один миллиметр или один сантиметр и т.д. На графике каждой точке кривой соответствует группа женщин, рост которых лежит в пределах сантиметра (по полсантиметра в обе стороны от указанной цифры). Средняя высота, женщин, как видно из гистограммы, равна 162,5 см – это второй параметр. Третьим параметром является ширина колокола, которая в этом случае равна 12,5 см. Знание ширины кривой позволяет сразу же оценить, с какими отклонениями от среднего можно встретиться.
Рис. 12. Гистограмма роста женщин, к которой может быть подогнана нормальная кривая. В данной выборке было 1375 женщин.
Кривая (рис. 12) сходит на нет близ отметок слишком низкого (ниже 140 сантиметров) и слишком высокого роста – выше 180 сантиметров. Это, разумеется, не означает, что цифры большего или меньшего роста совсем уж нереальны: на волейбольной и баскетбольной площадках встречаются очень высокие девушки. И, тем не менее, можно смело брать на вооружение правило: отклонения от среднего, больше трех полуширин гауссианы, встречается очень редко – с вероятностью около 0,27 % (правило трех сигм).
Знание среднего значения случайной величины и ширины кривой нормального распределения позволяет уверенно отделить возможное от невозможного. В свое время Анри Пуанкаре заметил с сарказмом, что все верят в универсальность нормального распределения: физики верят потому, что думают – математики доказали его логическую необходимость, а математики верят, так как считают, что физики проверили это лабораторными экспериментами. Не будем спорить с известным ученым, а просто рассмотрим результаты некоторых исследований, где достаточно убедительно показаны возможность подчинения самых различных процессов нормальному закону. 1. Понятие «мелиорация» (от латинского melioration – улучшение) чрезвычайно широко по смыслу: оно может обозначать любой вид улучшения почв, но чаще всего под мелиорацией понимают орошение и осушение, т.е. регулирование количества воды в почве. Однако прежде чем проводить мелиоративные работы необходимо установить ту оптимальную степень осушения, тот предел содержания влаги в почве, к достижению которого должны стремиться мелиораторы. Возникает вопрос: каков он? Естественно, что лучше всего на этот вопрос может ответить само растение, для возделывания которого и предпринимается улучшение земель. Так в чем же нуждается растение? Ему необходимы воздух, вода, тепло и питательные вещества, причём в соответствии с биологическим законом незаменимости действия факторов внешней среды растение не может нормально развиваться, если даже только один из этих факторов окажется в недостаточном количестве. По счастью, все они как-то связаны между собой, и, регулируя, например, содержание воды в почве, можно одновременно влиять и на воздушный режим растения и в какой-то степени на тепловой и питательный режимы. Интересно отметить, что растение, по сути дела, одинаково отзывается на изменение каждого из этих факторов. Представим, например, зависимость урожая растения от запасов влаги в почве в виде кривой (рис. 13). Такая кривая может быть построена по данным опыта, в ходе которого остальные условия сохраняются постоянными.
Рис. 13. Кривая зависимости урожая растения от запасов влаги в почве.
Из рисунка следует, что для получения хоть какого-нибудь урожая необходим начальный запас влаги в почве, определяемый величиной Wmin. С увеличением запаса влаги урожай повышается, пока не достигнет наибольшего значения Umax. Дальнейшее увеличение влажности почвы, наоборот, ведет к снижению урожая. Запас влаги, при котором получен наибольший урожай, является оптимальным. Но точно такой же характер кривой дают и графики зависимости урожая от тепла или от количества питательных веществ в почве. Отметив эту одинаковость кривых, в шестидесятых годах прошлого столетия советский исследователь В.В. Шабанов нанес на график, построенный в безразмерных координатах, данные опытов, проведенных различными исследователями в течение почти пятидесяти лет. В опытах изучались совершенно различные растения и влияние разных факторов на их урожай. Однако все опытные точки легли вблизи некоторой колоколообразной кривой (рис. 14), в которой нетрудно угадать кривую нормального распределения. По виду кривой (рис. 14) легко заключить, что требования растений к условиям внешней среды не слишком категоричны: в пределах диапазона D отклонение тех или иных факторов от оптимального их значения мало влияет на величину урожая. Отсюда, например, следует, что не столь уж обязательно обеспечивать растению оптимальный водный режим. Вполне достаточно поддерживать влажность почвы в пределах диапазона, гарантирующего устойчиво высокий урожай.
Рис. 14. Кривая распределения влияния факторов на урожайность растения.
2. Для создания новой конструкции обуви массового производства требуются знания в области анатомии и физиологии стопы, законов варьирования размеров стоп населения, а также знакомство с вопросами биомеханики. Все это необходимо для правильного построения внутренней формы обуви, чтобы при массовом выпуске на «неизвестного» потребителя каждый мог подобрать себе вполне удобную для носки обувь. Это довольно сложная задача, так как форма и размеры стоп людей сильно колеблются даже в пределах, казалось бы, однородной группы населения. По условиям массового производства, конечно, желательно выпускать по возможности однотипную продукцию. Поэтому приходится искать компромиссное решение: установить такие размеры и формы обуви, чтобы при минимальном их количестве достигалась максимальная удовлетворенность населения. Для этого используют стандартизацию форм колодок, по которым производится обувь. Чтобы разработать такие стандартные колодки, необходимо проделать очень большую работу: узнать какие размеры и форму имеют стопы определенных групп населения страны, учесть размеры стоп детей разных возрастов в городах и селах и т.д. Обработка результатов статистических данных позволила установить зависимость между основными размерными признаками стоп. Так, оказалось, что у стоп средних размеров имеется связь между длиной стопы и её шириной, длиной стопы и обхватом в плюсне – фаланговом сочленении, шириной стопы в этом месте и шириной в пятке и т.д. Если графически представить результаты обмера стопы у весьма большого числа людей, то получится кривая нормального распределения (рис. 15). Количество стоп средних размеров будет максимальным, а количество стоп очень малых и очень больших размеров – крайне мало. Следовательно, и обувь по размерам нужно изготавливать в таких относительных количествах, в каких распределяются стопы по длине.
Рис. 15. Кривая распределения длин стоп у женщин.
Закон нормального распределения действует и в отношении других размеров стопы, например, обхвата в пучках (рис. 16) и т.д.
Рис. 16. Кривая распределения женских стоп по обхвату.
3. При проведении открытых горных работ применяется шарошечное бурение пород. Оценку буримости горных пород производят на основе длительной непрерывной регистрации энергоемкости и скорости бурения. Скорость бурения, применяемая в настоящее время в качестве характеристики буримости пород, фактически является параметром, отражающим конструктивные возможности бурового станка. Энергоемкость процесса бурения объективно отражает прочность пород и может служить надежным критерием оценки их буримости. Эти выводы сделаны в результате массового сопоставления энергоемкости и скорости бурения на различных карьерах. Массовые измерения энергоемкости и скорости бурения показали также, что построение непрерывных функций распределения этих параметров дает объективную характеристику прочностных свойств пород месторождений.
Рис. 17. Распределение пород по удельной энергоемкости шарошечного бурения по карьерам.
Рис. 18. Распределение пород по механической скорости бурения по карьерам.
На рис. 17, 18 представлены кривые распределения пород по энергоемкости и скорости бурения, составленные на основании измерения этих параметров по трем карьерам (I, II, III – условные обозначения карьеров). Как видно из рисунков, кривые близки к нормальному закону распределения Гаусса, что позволяет использовать модальные значения функций в качестве средней величины характеризуемого признака для всего месторождения. 4. В глазу человека имеются нервные клетки трех видов, различающихся чувствительностью к лучам разных цветов, как это показано на графике (рис. 19). Каждому виду соответствует своя кривая. Клетки первого вида наиболее раздражаются синими лучами (1), второго – зелеными (2), третьего – красными (3).
Рис. 19. Кривые чувствительности.
На рис. 20 представлена так называемая кривая видности. Установлено, что наиболее сильное ощущение в центральной зоне сетчатки глаза вызывают желто-зеленые лучи с длиной волны около 0,56 мкм. Принимая силу этого ощущения за единицу, можно описать графиком (1) ощущения от лучей другой окраски.
Рис. 20. Кривая видности.
Как видно из рисунков распределение раздражения нервных клеток для всех цветов в зависимости от длины волны подчиняется нормальному закону. 5. Носители заряда в полупроводнике в любой момент времени характеризуются координатами и скоростями (квазиимпульсом) каждого из них. Эту громоздкую информацию удобно представить в компактном виде, вводя функцию распределения f(v, z, t), которая определяет состояние всей системы. Функция распределения показывает, какая часть электронов или дырок в момент времени t имеет скорость v и координату r (или вероятность иметь скорость v и координату r в момент времени t). Из функции распределения можно получить практически все важные средние характеристики носителей заряда: дрейфовую и тепловую скорости, среднюю энергию и коэффициент диффузии. Изменение функции характеризует эволюцию ансамбля носителей заряда во времени. Динамику функции распределения описывает фундаментальное уравнение Больцмана (кинетическое уравнение). Решение уравнения Больцмана есть задача физической кинетики, в том числе и кинетики полупроводников. В отсутствии внешних возмущений решением кинетического уравнения будет максвелловская функция распределения со средней энергией носителей заряда, соответствующей температуре решетки. Если на систему носителей заряда воздействуют внешние электрические или магнитные поля, температура носителей заряда начинает отличаться от температуры решетки. В этом случае говорят о горячих электронах и/или дырках. В этой связи возникает необходимость в определении, наряду с другими характеристиками, коэффициента диффузии горячих электронов. Коэффициент диффузии связан со средним квадратическим смещением частицы в координатном пространстве. Для вычисления средних квадратических смещений вся моделируемая траектория электрона разбивается на части с равной продолжительностью во времени t и определяются отрезки расстояний, на которые сместилась частица в течение каждого такого промежутка t. Определенный таким образом коэффициент диффузии зависит от величины t, когда t меньше некоторого максимального значения t0. При этом распределение отрезков расстояний при t > t0 подчиняется нормальному закону, т.е. имеет гауссовскую форму (рис. 21)
Рис. 21.
6. Неисчерпаемость электрона, провозглашенная в начале ХХ века, привела к открытию множества элементарных частиц к одной из которых относится и так называемый ρ-мезон.
Рис. 22. Кривая вероятности рождения частицы ρ-мезон. На рис. 22 представлена кривая вероятности рождения этой частицы. Она показывает зависимость этой вероятности от суммарной энергии электрона и позитрона, сливающихся в ρ-мезон. Над узким интервалом шкалы энергий этот пик возвышается подобно резонансной кривой. Именно поэтому частицы, которым свойственна такая закономерность, называются резонансами. Интересна история этого графика, полученного впервые сибирскими физиками в 1967 году. Группа французских исследователей в Орсэ год спустя повторила их эксперимент и получила несколько иной результат. Однако, затем другая исследовательская группа, в том же Орсэ, провела новый, более точный эксперимент и на этот раз точки аккуратно легли на новосибирскую кривую.
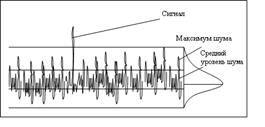
7. В технике беспорядочные колебания случайной величины около её среднего значения называют «шумом». Такой шум, например, можно услышать, сняв телефонную трубку или включив радиоприемник. Если шум записать на экране, то возникает беспорядочная зигзагообразная кривая (рис. 23).
Рис. 23. Сигнал ядерного магнитного резонанса на фоне так называемого «белого шума». Шум создается флуктуациями токов в сложной электронной схеме, регистрирующий резонанс.
Нетрудно ограничить «график шума» двумя горизонтальными линиями, так сказать, вписать весь шум между нулем и некоторым максимумом. Что же это за верхний предел шума? Чтобы его оценить, необходимо сначала ввести понятие среднего уровня шума: просматривая все более пространные участки кривой, можно наметить горизонтальную прямую, площадь под которой равнялась бы площади под кривой шума на данном отрезке графика. Чем шире просмотренный участок, тем точнее будет определяться средний уровень (на рисунке он отмечен пунктиром, проведенным на высоте 0,8), и тем увереннее будет подтверждаться закономерность, бросающаяся в глаза уже при первом взгляде на кривую: верхний предел превышает средний уровень примерно в четыре раза. Это вполне объяснимо: колокол гауссовой кривой обрывается исключительно резко, несмотря на то, что с точки зрения формальной математики гауссова кривая продолжается в бесконечность. Маловероятное становится невозможным, и всякий заметный выступ графика над граничной горизонталью – это уже не шум, это уже сигнал. 8. На рисунках 24, 25 представлены график распределения скоростей в турбулентном следе вдалеке за телом в случае движения, график распределения концентрации примеси в турбулентном потоке, а на рисунке 26 показан закон распределения структурной вязкости η цементного раствора. На графиках сплошные линии – результаты теоретических расчетов; точки – экспериментальные данные.
Рис. 24. График распределения скоростей в турбулентном следе.
Рис. 25. Плотность распределения вероятностей концентрации примеси в турбулентной жидкости.
Рис. 26. Закон распределения структурной вязкости цементного раствора.
Как видно из приведенных рисунков все отмеченные процессы подчинены нормальному закону. При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. С этой целью вводят специальные характеристики, в частности, асимметрию и эксцесс. Для нормального распределения эти характеристики равны нулю. Поэтому, если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот, большие значения асимметрии и эксцесса указывают на значительное отклонение от нормального. Оценку асимметрии осуществляют с помощью формулы
где μ3 – момент третьего порядка,
Рис. 27. Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от М(Х), и отрицательна наоборот (рис. 27). Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума функции). Примером асимметричного распределения может служить график распределения пассажиров метрополитена по длительности поездок в Москве (рис. 28).
Рис. 28. Распределение пассажиров метрополитена по дальности поездок в Москве: 1 – 1946, 2 – 1954, 3 – 1959, 4 –1964 гг.
На графике показано, как в зависимости от дальности поездок распределяются перевозки пассажиров в московском метрополитене. Чем дальше расположена станция метро от центра города, тем выше средняя дальность поездок пассажиров, следующих от этой станции. С увеличением длины сети метро возрастает дальность поездок пассажиров, и кривые распределения сдвигаются дальше от оси абсцисс. В заключении отметим, что в разделе «Законы распределения» представлен пример построения нормальной кривой по опытным данным.
Показательное распределение
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью
где l - постоянная положительная величина. Из (11) видно, что показательное распределение определяется одним параметром l > 0. Найдем функцию распределения F(x)
Итак,
Графики для (11) и (12) показаны на рис. 29.
Рис. 29.
Интегрируя (1) по частям, положив u = x, du = dx,
Математическое ожидание показательного распределения равно обратной величине параметра l. Найдем дисперсию
Дважды интегрируя по частям, получим
Следовательно,
Среднее квадратическое отклонение
Сравнивая (*) и (**), заключаем, что М(Х) = s(Х) = 1/l, то есть математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой. Упражнения 1. Все значения равномерно распределенной случайной величины принадлежат отрезку [4, 10]. Найти вероятность попадания случайной величины в промежуток (5, 8). 2. Трамваи данного маршрута идут с интервалом 5 минут. Пассажир подходит к трамвайной остановке в некоторый момент времени. Какова вероятность появления пассажира не ранее чем через минуту после ухода предыдущего трамвая, но не позднее чем за две минуты до отхода следующего трамвая. 3. Случайная величина Х распределена по нормальному закону с математическим ожиданием M(Х) = 40 и дисперсией D(Х) = 200. Найти вероятность попадания случайной величины в интервал (30, 80). 4. Считается, что отклонение длины изготавливаемых деталей от стандарта является случайной величиной, распределенной по нормальному закону. Если стандартная длина равна а = 400 мм и среднее квадратическое отклонение 5. Случайная величина Х подчинена нормальному закону с математическим ожиданием 6. Случайная величина Х подчинена нормальному закону с математическим ожиданием а = 0 (рис. 13).
Рис. 13.
Задан интервал (a, b), не включающий начала координат. При каком значении s вероятность попадания случайной величины Х в интервал (a, b) достигает максимума.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.183.122 (0.012 с.) |

















 ,
, – среднее квадратическое отклонение.
– среднее квадратическое отклонение.



 (11)
(11) .
. (12)
(12)
 . (1)
. (1) ,
,  , получим
, получим . (*)
. (*)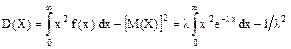 .
. .
. .
.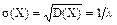 . (**)
. (**) , то какую точность длины изделия можно гарантировать с вероятностью 0,8?
, то какую точность длины изделия можно гарантировать с вероятностью 0,8? и средним квадратическим отклонением s(Х) = s. Вычислить с точностью до 0,01 вероятности попадания случайной величины на участки (а, а + s), (а + s, а + 2s), (а + 2s, а + 3s).
и средним квадратическим отклонением s(Х) = s. Вычислить с точностью до 0,01 вероятности попадания случайной величины на участки (а, а + s), (а + s, а + 2s), (а + 2s, а + 3s).