
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 5. Статическое распределение выборки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Раздел 1. Основные понятия и теоремы теории вероятностей
1. Задания для самостоятельной работы 1. Изучить теоретический материал по теме «Элементы комбинаторики» по вопросам: 1.1. Основные формулы и правила комбинаторики 1.2. Комбинации-перестановки 1.3. Комбинации-размещения 1.4. Комбинации сочетания 2. Изучить теоретический материал по темам «Достоверные, невозможные, случайные события. Алгебра событий. Теоремы умножения вероятностей для независимых и зависимых событий. Полная группа событий. Формула полной вероятности. Формула Байеса. Повторные независимые испытания. Формула Бернулли» по вопросам: 1.1. Алгебра событий. Виды случайных событий 1.2. Аксиоматическое определение вероятности. Вероятностное пространство 1.3. Классическая схема вычисления вероятности 1.4. Теоремы сложения и умножения вероятностей 1.5. Формула полной вероятности 1.6. Формулы Байеса 1.7. Схема независимых повторных испытаний 1.8. Закон больших чисел 2. Выполнить задания: Задача №1 Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз? Задача №2 Сколько можно составить сигналов из шести флажков различного цвета, взятых по 2? Задача №3 Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей? Задача №4 Студент ищет формулу в трех справочниках. Пусть
Задача №5 Брошены 2 игральные кости. Описать пространство элементарных событий этого эксперимента и найти вероятности следующих событий: а) сумма выпавших очков равна 8; б) сумма очков равна 6, а произведение 9; в) сумма очков не превышает 5; г) разность очков меньше 2; д) сумма очков расположена в промежутке [4; 10]. Задача №6 В ящике имеется 16 деталей, среди которых 4 бракованные. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что: а) извлеченные детали качественные; б) среди извлеченных деталей 2 бракованные.
Задача №7 Вероятность возникновения трещин в железобетонных формах в процессе их изготовления равна 0,1. Если трещина образовалась, то форма бракуется с вероятностью 0,9. Найти вероятность того, что две наудачу выбранные формы не будут забракованы. Задача №8 Рабочий обслуживает три станка. Вероятность того, что в течение часа станок потребует внимания рабочего для 1-го станка равна 0,25, для 2-го – 0,4, для 3-го – 0,15. Найти вероятность того, что внимания рабочего потребуют точно два станка. Задача №9 Вероятность попадания стрелком в мишень при одном выстреле равна 0,8. Найти вероятность того, что при 4 выстрелах стрелок попадает: а) не более одного раза, б) ни одного раза, в) хотя бы один раз. Задача №10 В первой урне содержится 11 шаров, из них 6 белых. Во второй урне содержится 19 шаров, из них 4 белых. Из первой урны наудачу извлекли один шар и переложили во вторую. Найти вероятность того, что извлеченный после этого шар из второй урны окажется белым. Задача №11 Пассажир берет билет в одной из трех касс с вероятностями: 0,3; 0,2; 0,5. Вероятности того, что билеты к моменту прихода пассажира будут в кассе распроданы равны соответственно 0,3; 0,15; 0,2. Пассажир направился в одну из касс и купил билет. Найти вероятность того, что это была первая касса. Задача №12 В каждом из 400 независимых повторных испытаний событие а) не менее 300 раз, б) более 240 раз, в) не менее 270 и не более 350 раз. II. Контрольные вопросы для самопроверки 1. Какие комбинации по m элементов, составленные из n различных элементов называют размещениями, а какие – сочетаниями? 2. Какой формулой определяется число сочетаний? 3. Как найти число перестановок из n элементов? 4. Какие виды случайных событий вы знаете? 5. Какой формулой определяется вероятность события при классическом определении? 6. Каковы основные свойства вероятности? 7. Какой формулой определяется вероятность суммы совместных событий? 8. Что такое условная вероятность? 9. По какой формуле вычисляют вероятность произведения независимых событий? 10. Какое равенство называют формулой полной вероятности? 11. По каким формулам можно переоценить вероятности гипотез после проведения испытания, в результате которого событие А появилось? 12. Как вычислить вероятность того, что в n испытаниях событие А осуществляется к раз и не осуществляется n – к раз?
Раздел 2. Случайные величины и их законы распределения.
1. Задания для самостоятельной работы
1. Изучить теоретический материал по темам «Случайная величина. Дискретная случайная величина (д.с.в.). Ряд распределения дискретной случайной величины. Функция распределения случайной величины и ее свойства. Математическое ожидание и дисперсия, их свойства, среднее квадратическое отклонение; моменты случайных величин: начальные, центральные моменты; мода, медиана, квантили. Некоторые законы распределения д.с.в.: геометрическое распределение, биноминальное распределение, распределение Пуассона. Непрерывная случайная величина (н.с.в.): плотность распределения и ее свойства. Некоторые законы распределения н.с.в.: равномерное распределение, нормальное, экспоненциальное распределение» по вопросам: 1.1. Закон распределения д.с.в. 1.2. Законы биноминальный и Пуассона 1.3. Числовые характеристики д.с.в., их свойства 1.4. Функция распределения вероятностей случайной величины 1.5. Плотность распределения вероятностей н.с.в, ее свойства 1.6. Числовые характеристики н.с.в. 1.7. Нормальное распределение 2. Выполнить задания: Задача №1
Найти
Задача №2
Цех изготовил 100 изделий. Вероятность того, что наугад взятое изделие бракованное равна 0,03. Составить закон распределения случайной величины Задача №3
Дана плотность распределения абсолютно непрерывной случайной величины
Найти
Задача №4
С.в.
Найти
Задача №5
Прибор производит измерение диаметра детали без систематических ошибок. Случайные ошибки измерения подчинены нормальному закону со средним квадратичным отклонением
II. Контрольные вопросы для самопроверки 1. Чем отличается дискретная случайная величина от непрерывной? 2. Какие способы задания дискретной случайной величины вы знаете? 3. Какая асимптотическая формула используется для случая малых значений р и больших значений n в серии n проводимых повторных испытаниях? 4. Что характеризует математическое ожидание случайной величины? 5. Какой формулой определяется математическое ожидание д.с.в.? 6. Как определяется дисперсия случайной величины? Что она характеризует? 7. Каковы основные свойства математического ожидания и дисперсии? 8. Что такое плотность н.с.в? 9. Каковы основные свойства функции распределения? 10. Как называется распределение вероятностей, если на интервале возможных значений случайной величины плотность распределения является постоянной? 11. Как определяется математическое ожидание для н.с.в.? 12. Каков вероятностный смысл параметров нормального распределения? 13. В чем заключается «правило трех сигм»?
Задача 1 В ходе эксперимента получены данные наблюдений:
Для данной выборки выполнить следующее: · Построить эмпирическую функцию распределения; · Вычислить числовые характеристики выборки (мода, медиана, выборочное среднее, выборочная дисперсия, среднее квадратическое отклонение, начальные и центральные моменты); · Определить тип распределения (симметричный – асимметричный, плосковершинный – островершинный).
Задача 1 Из генеральной совокупности извлечена выборка.
Найти несмещенные оценки генерального среднего и генеральной дисперсии.
Задача 2 В результате проведенных наблюдений получена выборка, ряд распределения которой имеет вид:
Считая, что генеральная совокупность имеет нормальное распределение, найти доверительные интервалы для ее математического ожидания и среднего квадратического отклонения с надежностью 0,95. Задача 1 Экзаменационный билет по математике содержит 10 заданий. Пусть
Оценить закон распределения случайной величины
Образовательные технологии В соответствии с требованиями ФГОС ВПО по направлению подготовки реализация компетентностного подхода в учебном курсе «Теория вероятностей и математическая статистика» предусматривает широкое использование активных и интерактивных форм проведения занятий в сочетании с внеаудиторной работой с целью формирования и развития профессиональных навыков обучающихся. Удельный вес занятий, проводимых в интерактивных формах, определяется главной целью ООП бакалавриата по направлению «Экономика», особенностью контингента обучающихся и содержанием учебного курса. В целом, их применение в учебном процессе предполагается не менее 20 % аудиторных занятий. Таким образом, согласно утвержденному учебному плану удельный вес занятий, проводимых в интерактивных формах, должен составлять не менее 12 часов.
7. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов
7.1. Примерная тематика рефератов и курсовых работ – не предусмотрено учебным планом. 7.2. Примерные вопросы для оценки качества освоения дисциплины на экзамене.
Раздел 1. Основные понятия и теоремы теории вероятностей Что является предметом изучения дисциплины? Каковы цели и задачи дисциплины? Какова связь теории вероятностей и математической статистики? Дать определение пространства элементарных исходов, стохастического эксперимента, события. Дать классическое определение вероятности. Дать аксиоматическое определение вероятности. Сформулировать и доказать теоремы сложения вероятностей для совместных и несовместных событий. Дать определение зависимых событий и условной вероятности. Сформулировать и доказать теоремы умножения вероятностей. Вывести формулу полной вероятности и указать условия ее применения. Записать формулу Байеса и указать условия ее применения. Что понимается под схемой Бернулли? Формула Бернулли. Формула Пуассона, доказательство, условия ее применения. Сформулировать локальную теорему Муавра-Лапласа и указать условия ее использования. Сформулировать интегральную теорему Муавра-Лапласа. Вариант 0 1. В группе 15 студентов, среди которых 9 отличников. По списку наудачу отобраны 7 студентов. Найти вероятность того, что среди отобранных студентов четыре отличников. 2. В читальном зале имеется семь учебников по теории вероятностей, из которых пять в переплете. Библиотекарь наудачу взял три учебника. Найти вероятность того, что три учебника окажутся в переплете. 3. В семье шесть детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) более двух мальчиков. Вероятность рождения мальчика принять равной 0,51. 4. Дан закон распределения дискретной случайной величины:
вычислить ее математическое ожидание, дисперсию и среднее квадратическое отклонение. 5. Дана функция распределения непрерывной случайной величины Х F(x)= Найти плотность распределения f(x), построить ее график, вероятность попадания в заданный интервал,, Mx, Dx, 6. Задано распределение вероятностей дискретной двумерной случайной величины:
Найти законы распределения составляющих, коэффициент корреляции.
8. Учебно-методическое и информационное обеспечение дисциплины
Раздел 1. Основные понятия и теоремы теории вероятностей
1. Задания для самостоятельной работы 1. Изучить теоретический материал по теме «Элементы комбинаторики» по вопросам: 1.1. Основные формулы и правила комбинаторики 1.2. Комбинации-перестановки 1.3. Комбинации-размещения 1.4. Комбинации сочетания 2. Изучить теоретический материал по темам «Достоверные, невозможные, случайные события. Алгебра событий. Теоремы умножения вероятностей для независимых и зависимых событий. Полная группа событий. Формула полной вероятности. Формула Байеса. Повторные независимые испытания. Формула Бернулли» по вопросам: 1.1. Алгебра событий. Виды случайных событий 1.2. Аксиоматическое определение вероятности. Вероятностное пространство 1.3. Классическая схема вычисления вероятности 1.4. Теоремы сложения и умножения вероятностей 1.5. Формула полной вероятности 1.6. Формулы Байеса 1.7. Схема независимых повторных испытаний 1.8. Закон больших чисел 2. Выполнить задания: Задача №1 Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз? Задача №2 Сколько можно составить сигналов из шести флажков различного цвета, взятых по 2? Задача №3 Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей? Задача №4 Студент ищет формулу в трех справочниках. Пусть
Задача №5 Брошены 2 игральные кости. Описать пространство элементарных событий этого эксперимента и найти вероятности следующих событий: а) сумма выпавших очков равна 8; б) сумма очков равна 6, а произведение 9; в) сумма очков не превышает 5; г) разность очков меньше 2; д) сумма очков расположена в промежутке [4; 10]. Задача №6 В ящике имеется 16 деталей, среди которых 4 бракованные. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что: а) извлеченные детали качественные; б) среди извлеченных деталей 2 бракованные.
Задача №7 Вероятность возникновения трещин в железобетонных формах в процессе их изготовления равна 0,1. Если трещина образовалась, то форма бракуется с вероятностью 0,9. Найти вероятность того, что две наудачу выбранные формы не будут забракованы. Задача №8 Рабочий обслуживает три станка. Вероятность того, что в течение часа станок потребует внимания рабочего для 1-го станка равна 0,25, для 2-го – 0,4, для 3-го – 0,15. Найти вероятность того, что внимания рабочего потребуют точно два станка. Задача №9 Вероятность попадания стрелком в мишень при одном выстреле равна 0,8. Найти вероятность того, что при 4 выстрелах стрелок попадает: а) не более одного раза, б) ни одного раза, в) хотя бы один раз. Задача №10 В первой урне содержится 11 шаров, из них 6 белых. Во второй урне содержится 19 шаров, из них 4 белых. Из первой урны наудачу извлекли один шар и переложили во вторую. Найти вероятность того, что извлеченный после этого шар из второй урны окажется белым. Задача №11 Пассажир берет билет в одной из трех касс с вероятностями: 0,3; 0,2; 0,5. Вероятности того, что билеты к моменту прихода пассажира будут в кассе распроданы равны соответственно 0,3; 0,15; 0,2. Пассажир направился в одну из касс и купил билет. Найти вероятность того, что это была первая касса. Задача №12 В каждом из 400 независимых повторных испытаний событие а) не менее 300 раз, б) более 240 раз, в) не менее 270 и не более 350 раз. II. Контрольные вопросы для самопроверки 1. Какие комбинации по m элементов, составленные из n различных элементов называют размещениями, а какие – сочетаниями? 2. Какой формулой определяется число сочетаний? 3. Как найти число перестановок из n элементов? 4. Какие виды случайных событий вы знаете? 5. Какой формулой определяется вероятность события при классическом определении? 6. Каковы основные свойства вероятности? 7. Какой формулой определяется вероятность суммы совместных событий? 8. Что такое условная вероятность? 9. По какой формуле вычисляют вероятность произведения независимых событий? 10. Какое равенство называют формулой полной вероятности? 11. По каким формулам можно переоценить вероятности гипотез после проведения испытания, в результате которого событие А появилось? 12. Как вычислить вероятность того, что в n испытаниях событие А осуществляется к раз и не осуществляется n – к раз?
Раздел 2. Случайные величины и их законы распределения.
1. Задания для самостоятельной работы
1. Изучить теоретический материал по темам «Случайная величина. Дискретная случайная величина (д.с.в.). Ряд распределения дискретной случайной величины. Функция распределения случайной величины и ее свойства. Математическое ожидание и дисперсия, их свойства, среднее квадратическое отклонение; моменты случайных величин: начальные, центральные моменты; мода, медиана, квантили. Некоторые законы распределения д.с.в.: геометрическое распределение, биноминальное распределение, распределение Пуассона. Непрерывная случайная величина (н.с.в.): плотность распределения и ее свойства. Некоторые законы распределения н.с.в.: равномерное распределение, нормальное, экспоненциальное распределение» по вопросам: 1.1. Закон распределения д.с.в. 1.2. Законы биноминальный и Пуассона 1.3. Числовые характеристики д.с.в., их свойства 1.4. Функция распределения вероятностей случайной величины 1.5. Плотность распределения вероятностей н.с.в, ее свойства 1.6. Числовые характеристики н.с.в. 1.7. Нормальное распределение 2. Выполнить задания: Задача №1
Найти
Задача №2
Цех изготовил 100 изделий. Вероятность того, что наугад взятое изделие бракованное равна 0,03. Составить закон распределения случайной величины Задача №3
Дана плотность распределения абсолютно непрерывной случайной величины
Найти
Задача №4
С.в.
Найти
Задача №5
Прибор производит измерение диаметра детали без систематических ошибок. Случайные ошибки измерения подчинены нормальному закону со средним квадратичным отклонением
II. Контрольные вопросы для самопроверки 1. Чем отличается дискретная случайная величина от непрерывной? 2. Какие способы задания дискретной случайной величины вы знаете? 3. Какая асимптотическая формула используется для случая малых значений р и больших значений n в серии n проводимых повторных испытаниях? 4. Что характеризует математическое ожидание случайной величины? 5. Какой формулой определяется математическое ожидание д.с.в.? 6. Как определяется дисперсия случайной величины? Что она характеризует? 7. Каковы основные свойства математического ожидания и дисперсии? 8. Что такое плотность н.с.в? 9. Каковы основные свойства функции распределения? 10. Как называется распределение вероятностей, если на интервале возможных значений случайной величины плотность распределения является постоянной? 11. Как определяется математическое ожидание для н.с.в.? 12. Каков вероятностный смысл параметров нормального распределения? 13. В чем заключается «правило трех сигм»?
Раздел 5. Статическое распределение выборки.
1. Задания для самостоятельной работы 1. Изучить теоретический материал по темам «Генеральная и выборочная совокупности. Вариационные ряды: дискретные и интервальные. Оценка функции распределения и плотности распределения: эмпирическая функция распределения, гистограмма, полигон, кумулятивная кривая» по вопросам: 1.1. Генеральная и выборочная совокупности 1.2. Статистическое распределение выборки 1.3. Полигон и гистограмма 1.4. Несмещенные, эффективные и состоятельные оценки 1.5. Выборочная средняя 1.6. Выборочная дисперсия 2. Выполнить задания: Задача 1 В ходе эксперимента получены данные наблюдений:
Для данной выборки выполнить следующее: · Построить эмпирическую функцию распределения; · Вычислить числовые характеристики выборки (мода, медиана, выборочное среднее, выборочная дисперсия, среднее квадратическое отклонение, начальные и центральные моменты); · Определить тип распределения (симметричный – асимметричный, плосковершинный – островершинный).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 775; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.015 с.) |

 – событие, означающее, что нужная формула содержится в i -м справочнике. Выразить через
– событие, означающее, что нужная формула содержится в i -м справочнике. Выразить через  следующие события:
следующие события: – формула содержится только в одном справочнике;
– формула содержится только в одном справочнике; – формулы нет ни в одном справочнике;
– формулы нет ни в одном справочнике;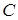 – формула содержится хотя бы в одном справочнике.
– формула содержится хотя бы в одном справочнике. , если с.в.
, если с.в.  имеет следующий закон распределения:
имеет следующий закон распределения:
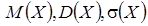 .
. .
. . Построить графики
. Построить графики 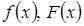 .
. .
.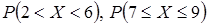 .
. мм. Какова вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 10 мм.
мм. Какова вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 10 мм.


 .
.
 .
.


