
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение нормальной кривой по опытным даннымСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть дано статистическое распределение в виде последовательности интервалов и соответствующих им частот (относительных частот), которая имеет гистограмму, изображенную на рис. 31.
Полагая
Нанесенные на гистограмму точки
Один из способов построения нормальной кривой по данным наблюдений состоит в следующем: 1) находят 2) находят ординаты yi (выравнивающие частоты) теоретической кривой по формуле
где 3) строят точки (xi, yi) в прямоугольной системе координат и соединяют их плавной кривой. Пример. Дано статистическое распределение
Показать, что оно близко к нормальному распределению, и построить график. Решение. Здесь n = 50. Найдем середины интервалов и составим таблицу
Так как математическое ожидание М(Х) = а и среднее квадратическое отклонение s(Х) = s неизвестны, то в качестве оценок этих параметров примем соответственно выборочную среднюю
Контроль:
Найдем условные эмпирические моменты первого и второго порядков
Найдем шаг h = 10,5 - 7,5 = 3. Отсюда
Составим расчетную таблицу
Прежде чем построить кривую дадим пояснения по поводу последнего столбца таблицы. Выясним вероятностный смысл плотности распределения f(x) Если F(x) функция распределения непрерывной случайной величины Х, то по определению f(x) =
Разность F(x + Dx) - F(x), как уже известно, определяет вероятность того, что Х примет значение, принадлежащее интервалу (х, x + Dx). Таким образом, предел отношения вероятности того, что непрерывная случайная величина примет значение, принадлежащее интервалу (х, x + Dx), к длине этого интервала Dx (Dx ® 0) равен значению плотности распределения в точке х. Итак, функция f(x) определяет плотность распределения вероятности для каждой точки х. Из дифференциального исчисления известно, что приращение функции приближенно равно дифференциалу функции, то есть
или
Так как
Из (*) следует: вероятность того, что случайная величина примет значение, принадлежащее интервалу Итак, произведение в последнем столбце f(x) Dx = f(x) h определяет приближенно вероятность попадания Х в интервал Dx = h. Теперь, используя данные таблицы, построим кривую по точкам (xi, yi) в прямоугольной системе координат (рис. 32).
Сопоставим полученные результаты с вероятностями попадания случайной величины на данный участок, вычисляемый по формуле
где Ф(х) - функция Лапласа, значения которой табулированы в Приложении 2.
Из результатов расчетов следует, что h f(x)» P. Составим таблицу относительных частот.
Сравнивая значения W и hf(x) (или W и P), убеждаемся в том, что заданное статистическое распределение можно считать подчиненным нормальному закону. Элементы теории корреляции
Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Y от одной или нескольких других величин. Две случайные величины могут быть связаны либо функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми. Строгая функциональная зависимость реализуется редко, так как обе величины или одна из них подвержены еще действию случайных факторов, причём среди них могут быть и общие для обеих величин (под «общими» здесь подразумеваются такие факторы, которые воздействуют и на Y и на Х). В этом случае возникает статистическая зависимость. Например, если Y зависит от случайных факторов z1, z2, v1, v2, а Х зависит от случайных факторов z1, z2, u1, то между Y и Х имеется статистическая зависимость, так как среди случайных факторов есть общие, а именно: z1 и z2. Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае статистическую зависимость называют корреляционной. Приведем пример случайной величины Y, которая не связана с величиной Х функционально, а связана корреляционно. Пусть Y - урожай зерна, Х - количество удобрений. С одинаковых по площади участков земли при равных количествах внесенных удобрений снимают различный урожай, то есть Y не является функцией от Х. Это объясняется влиянием случайных факторов (осадки, температура воздуха и др.). Вместе с тем опыт показывает, что средний урожай является функцией от количества удобрений, то есть Y связан с Х корреляционной зависимостью. Корреляционная зависимость между двумя случайными величинами может быть как линейной, так и нелинейной. Линейная регрессия
Пусть Х и Y - зависимые случайные величины. Представим одну величину как функцию другой. Так как среди различных видов корреляционных зависимостей наиболее важными являются линейные, то мы ограничимся приближенным представлением величины Y в виде линейной функции величины Х, то есть
где a и b - параметры, подлежащие определению. Параметры a и b можно определить различными способами. Наиболее распространенный - метод наименьших квадратов. Функцию Имеет место следующая теорема. Теорема. Линейная средняя квадратическая регрессия Y на Х имеет вид
где mx = M(X), my = M(Y), Величина rxy называется коэффициентом корреляции величин Х и Y. Коэффициент корреляции равен
где mху - корреляционный момент случайных величин Х и Y, равный математическому ожиданию произведения отклонений этих величин, то есть
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 810; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.005 с.) |

 , i = 1, 2, …, n, составим таблицу
, i = 1, 2, …, n, составим таблицу ,
,  , …,
, …,  , где h - шаг таблицы, соединяем плавной кривой.
, где h - шаг таблицы, соединяем плавной кривой. Если полученная плавная кривая близка к кривой Гаусса, то можно обработать статистические данные с помощью нормального закона распределения.
Если полученная плавная кривая близка к кривой Гаусса, то можно обработать статистические данные с помощью нормального закона распределения.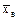 и
и  , например, по методу произведений;
, например, по методу произведений; ,
, ,
, 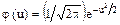 ;
;
 = 205
= 205
 = 305
= 305
 ,
,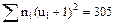 .
. ,
, 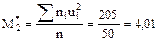 .
. ,
, ,
, ,
, .
.
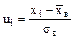

 , или в иной форме
, или в иной форме .
.
 .
. и dx = Dx, то
и dx = Dx, то . (*)
. (*) , приближенно равна (с точностью до бесконечно малых высшего порядка относительно Dx) произведению плотности вероятности в точке х на длину интервала Dx.
, приближенно равна (с точностью до бесконечно малых высшего порядка относительно Dx) произведению плотности вероятности в точке х на длину интервала Dx.
 ,
,
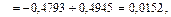


 ,
, ,
, ,
, ,
,  ,
, ,
, 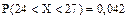 ,
, .
. , (1)
, (1) называют наилучшим приближением Y в смысле метода наименьших квадратов, если математическое ожидание
называют наилучшим приближением Y в смысле метода наименьших квадратов, если математическое ожидание  принимает наименьшее возможное значение. В этом случае функцию g(X) называют среднеквадратической регрессией Y на Х.
принимает наименьшее возможное значение. В этом случае функцию g(X) называют среднеквадратической регрессией Y на Х. , (2)
, (2) ,
,  .
. ,
, .
.


