
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выпуклость и вогнутость кривой.Содержание книги Поиск на нашем сайте
Точки перегиба. Рассмотри кривую Определение 1. Будем говорить, что кривая обращена выпуклостью вверх на интервале Кривая обращена выпуклостью вниз на интервале Кривая, обращённая выпуклостью вверх, называется выпуклой, а обращённая выпуклостью вниз – вогнутой. В этом разделе мы установим признаки, которые позволяют судить о направлении выпуклости графика Теорема 1. Если Доказательство. Пусть Как установлено ранее, уравнение касательной в точке
Нас интересует знак разности
Применяя т. Лагранжа к разности
и к разности производных опять применим ту же теорему
Рассмотрим теперь случай Пусть теперь Таким образом мы доказали, что Аналогично доказывается и Теорема 1’. Теорема 1’. Если Геометрическая интерпретация.

Если же Пример: установить интервалы выпуклости и вогнутости кривой.
Определение 2. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба этой кривой. Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой – над нею. Сформулируем теперь достаточные условия того, что данная точка является точкой перегиба. Теорема 2. Пусть кривая определяется уравнением Доказательство. 1)
Тогда, при 2) Пусть теперь Пример.
Асимптоты. Довольно часто требуется исследовать форму кривой Определение. Прямая А называется асимптотой кривой, если расстояние Различают вертикальные асимптоты – т.е. параллельные OY, горизонтальные – т.е. параллельные OX и наклонные, т.е. не параллельные OY или OX. I. Вертикальные асимптоты. Из определения следует, что если
то прямая Следовательно, для нахождения вертикальных асимптот нужно найти такие Пример.
т.к. при II. Наклонные асимптоты. Пусть (1) Определим коэффициенты (2) Пусть (2’) При этом из (2)
(3) Итак, если (1) есть асимптота, то выполняется (3) и, наоборот, если выполняется (3), то (1) – уравнение асимптоты. Определим теперь
Т.к.
Зная теперь
Итак, если (*) Обратное также справедливо. Если существуют пределы (*), то Пример. 1) Найдём вертикальные асимптоты:
2) Ищем наклонные асимптоты:
Пример.
при
Общий план исследования функций И построения графиков. Под «исследованием функции» обычно понимается нахождение: 1) естественной области существования функции; 2) точек разрыва функции; нули функции? 3) интервалов возрастания и убывания функции; 4) точек максимума и минимума и экстремальных значений функции; 5) областей выпуклости и вогнутости графика, точек перегиба; 6) асимптот графика функции. На основании проведённого исследования строится график. Целесообразно помечать элементы графика параллельно с исследованием. Замечание 1. Если Замечание 2. Если Замечание 3. Т.к. одни свойства функции могут определять другие, то порядок исследования можно изменять, исходя из конкретного вида исследуемой функции. Например, если Пример. Исследовать
|
|||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 671; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.232.137 (0.008 с.) |

 , которая является графиком однозначной, дифференцируемой функции
, которая является графиком однозначной, дифференцируемой функции  .
. , если все точки кривой лежат ниже любой касательной, проведенной к любой точке из этого интервала.
, если все точки кривой лежат ниже любой касательной, проведенной к любой точке из этого интервала. , если все её точки лежат выше любой её касательной на
, если все её точки лежат выше любой её касательной на  кривая
кривая  . Проведём касательную к графику
. Проведём касательную к графику  . Теорема будет доказана, если все точки
. Теорема будет доказана, если все точки  будет меньше ординаты у касательной при одном и том же значении
будет меньше ординаты у касательной при одном и том же значении  .
. имеет вид:
имеет вид: или
или .
. , которую можно записать в виде:
, которую можно записать в виде: .
. мы можем записать:
мы можем записать: (где С лежит между
(где С лежит между 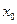 ), или
), или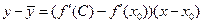 ,
,
 ,
,  между
между  и
и  . Тогда
. Тогда  ; т.к.
; т.к.  и
и  и по условию теоремы
и по условию теоремы  , т.е. Теорема 1 доказана.
, т.е. Теорема 1 доказана. , тогда
, тогда  . В этом случае
. В этом случае  и
и  , но
, но  и
и 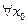
 ордината касательной больше ординаты графика
ордината касательной больше ординаты графика 
 , то кривая
, то кривая  есть
есть  - угла наклона касательной в точке с абсциссой
- угла наклона касательной в точке с абсциссой  Если
Если  убывает при возрастании
убывает при возрастании 
 возрастает при возрастании
возрастает при возрастании  - кривая выпукла.
- кривая выпукла. - кривая вогнута.
- кривая вогнута.
 , или
, или  не существует, и при переходе через
не существует, и при переходе через 
 меняет знак, то точка кривой с
меняет знак, то точка кривой с  при
при  и
и .
. есть точка перегиба.
есть точка перегиба. и
и  , тогда при
, тогда при  есть точка перегиба.
есть точка перегиба.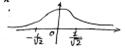

 (кривая Гаусса)
(кривая Гаусса) - нет точек перегиба
- нет точек перегиба , но при
, но при 
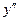 не существует.
не существует. расстояния от начала координат до этой точки) неограниченно приближается к некоторой прямой.
расстояния от начала координат до этой точки) неограниченно приближается к некоторой прямой.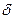 от точки
от точки  до этой прямой стремится к нулю.
до этой прямой стремится к нулю. ,
,
 . Тогда
. Тогда  ,
,  - асимптота, т.к.
- асимптота, т.к.  ,
, 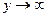 .
. - б.м. вертикальных асимптот,
- б.м. вертикальных асимптот, 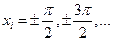 ,
, .
. .
. и
и  . Пусть
. Пусть 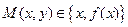 и
и  .
.  расстояние от
расстояние от 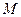 до
до  . По условию
. По условию

 - угол наклона
- угол наклона  из
из  ; т.к.
; т.к.  , то
, то .
. и (2’) приобретает вид:
и (2’) приобретает вид: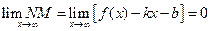 .
.
 или
или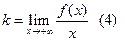

 есть асимптота,
есть асимптота, 

 - вертикальная асимптота.
- вертикальная асимптота.

 - асимптота.
- асимптота.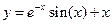 , вертикальных нет,
, вертикальных нет, 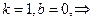
 при
при  ,
, асимптоты нет.
асимптоты нет.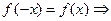 достаточно исследовать
достаточно исследовать  ОДЗ, т.к. график симметричен OY.
ОДЗ, т.к. график симметричен OY. также достаточно провести исследование для
также достаточно провести исследование для 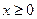 . График симметричен относительно начала координат.
. График симметричен относительно начала координат. и построить её график.
и построить её график.



