
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование функции на экстремумСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Исследование функции на экстремум с помощью второй производной. Пусть при Теорема. Пусть Доказательство. Пусть Т.к. Пусть теперь Если в Схема исследования.
Наибольшее и наименьшее значения функции на отрезке. Пусть Предположим, что Итак, То же самое можно сказать и о наименьшем значении Итак, если требуется найти наибольшее (наименьшее) значение непрерывной 1) Найти все max (min) 2) Вычислить значения 3) Из всех полученных выше значений выбрать наибольшее (наименьшее). Пример.
Формула Тейлора Предположим, что (1) Естественно предположить, то Будем искать (2)
(3) Подставляя теперь вместо
Подставляя теперь вместо (5) Обозначим теперь через
(6)
Т.о. (6) даёт возможность заменить Следующая задача – оценить
где Рассмотрим далее вспомогательную функцию от
Далее найдём
После сокращения получим (*) Итак,
остаточный член в форме Лагранжа. Т.к.
Формула
Если в формуле Тейлора положить (**) Этот частный случай формулы Тейлора называют формулой Маклорена.
Разложение по формуле Тейлора функций 1.
Подставляя эти значения в формулу (**) Маклорена, получим
Если
При
Здесь ошибка не превосходит Отметим, что для Действительно
Т.к.
Но
Следовательно, и Т.о. для 2.
Подставляя теперь эти значения в формулу Тейлора, получим
Т. к Применим полученную формулу для
Оценим теперь остаточный член:
Следовательно, ошибка меньше чем 3.
(х – в радианах).
Исследование функции на максимум и минимум С помощью формулы Тейлора. Ранее мы показали, что если при Предположим, что при x=a (1) Пусть также f(x) имеет непрерывные производные до (n+1) -го порядка включительно в окрестности x=a. Запишем для f(x) формулу Тейлора, учитывая (1): (2) Т.к. (2’) и рассмотрим различные возможные случаи. 1. n – нечётное а) б) 2. n – чётное Тогда n+1 – нечётное, и Если h достаточно мало по модулю, то Таким образом, если при
Если же
Пример. 1) Критические точки
Точки перегиба. Рассмотри кривую Определение 1. Будем говорить, что кривая обращена выпуклостью вверх на интервале Кривая обращена выпуклостью вниз на интервале Кривая, обращённая выпуклостью вверх, называется выпуклой, а обращённая выпуклостью вниз – вогнутой. В этом разделе мы установим признаки, которые позволяют судить о направлении выпуклости графика Теорема 1. Если Доказательство. Пусть Как установлено ранее, уравнение касательной в точке
Нас интересует знак разности
Применяя т. Лагранжа к разности
и к разности производных опять применим ту же теорему
Рассмотрим теперь случай Пусть теперь Таким образом мы доказали, что Аналогично доказывается и Теорема 1’. Теорема 1’. Если Геометрическая интерпретация.

Если же Пример: установить интервалы выпуклости и вогнутости кривой.
Определение 2. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба этой кривой. Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой – над нею. Сформулируем теперь достаточные условия того, что данная точка является точкой перегиба. Теорема 2. Пусть кривая определяется уравнением Доказательство. 1)
Тогда, при 2) Пусть теперь Пример.
Асимптоты. Довольно часто требуется исследовать форму кривой Определение. Прямая А называется асимптотой кривой, если расстояние Различают вертикальные асимптоты – т.е. параллельные OY, горизонтальные – т.е. параллельные OX и наклонные, т.е. не параллельные OY или OX. I. Вертикальные асимптоты. Из определения следует, что если
то прямая Следовательно, для нахождения вертикальных асимптот нужно найти такие Пример.
т.к. при II. Наклонные асимптоты. Пусть (1) Определим коэффициенты (2) Пусть (2’) При этом из (2)
(3) Итак, если (1) есть асимптота, то выполняется (3) и, наоборот, если выполняется (3), то (1) – уравнение асимптоты. Определим теперь
Т.к.
Зная теперь
Итак, если (*) Обратное также справедливо. Если существуют пределы (*), то Пример. 1) Найдём вертикальные асимптоты:
2) Ищем наклонные асимптоты:
Пример.
при
Общий план исследования функций И построения графиков. Под «исследованием функции» обычно понимается нахождение: 1) естественной области существования функции; 2) точек разрыва функции; нули функции? 3) интервалов возрастания и убывания функции; 4) точек максимума и минимума и экстремальных значений функции; 5) областей выпуклости и вогнутости графика, точек перегиба; 6) асимптот графика функции. На основании проведённого исследования строится график. Целесообразно помечать элементы графика параллельно с исследованием. Замечание 1. Если Замечание 2. Если Замечание 3. Т.к. одни свойства функции могут определять другие, то порядок исследования можно изменять, исходя из конкретного вида исследуемой функции. Например, если Пример. Исследовать
Кривизна плоской кривой.
Т.о. можно принять, что мера кривизны конечного участка гладкой (дифференцируемой) кривой должна быть прямо пропорциональна углу, на который поворачивается касательная при переходе от начальной точки дуги к конечной и обратно пропорциональна длине этой дуги. Поэтому, за меру кривизны конечной дуги (средняя кривизна) можно принять отношение угла поворота касательной к длине дуги. Пусть
Применим это определение к окружности радиуса
Т.к. длина дуги Т.о. кривизна любой дуги окружности есть const Вывод естественный: любая дуга при перемещении её по окружности всеми точками будет лежать на окружности. При этом с уменьшением R кривизна будет возрастать. Для кривых Поэтому, естественно от понятия средней кривизны на данном участке перейти к понятию кривизны кривой в данной точке, совершая предельный переход при
Определение. Кривизна кривой в точке есть производная от угла поворота касательной к кривой по длине дуги. При этом угол поворота касательной можно измерять разностью углов касательных с осью, например, Х. Выводим теперь формулу для вычисления кривизны кривой
Если не учитывать направление вогнутости кривой, то
Построим теперь окружность, которая имеет общую касательную с кривой в точке, общую кривизну и направление выгнутости. Такую окружность окружностью кривизны, её радиус – радиусом кривизны, а её центр – центром кривизны. Т.к. кривизна окружности обратна её R, то для радиуса кривизны получим (*) Центр кривизны
Рисунок соответствует случаю
Но (**) Т.к. Определение. Геометрическое место центров кривизны кривой | |||||||||||||||||
|
| Поделиться: |

 производная от
производная от  обращается в нуль, т.е.
обращается в нуль, т.е.  . Пусть, кроме того,
. Пусть, кроме того,  и непрерывна в окрестности
и непрерывна в окрестности  . Тогда справедлива
. Тогда справедлива имеет максимум, если
имеет максимум, если  и минимум, если
и минимум, если  .
. непрерывна, то
непрерывна, то  малый отрезок, содержащий
малый отрезок, содержащий  .
. убывает на выбранном отрезке
убывает на выбранном отрезке  . Но
. Но  , при
, при  и
и 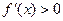 при
при  . Т.е. при переходе через
. Т.е. при переходе через  меняет знак с “+” на “-“, а это значит, что
меняет знак с “+” на “-“, а это значит, что  имеет в
имеет в  .
. в окрестности
в окрестности  при
при  изменяет знак с “-” на “+“, т.о. мы имеем в
изменяет знак с “-” на “+“, т.о. мы имеем в  .
. , то в этой точке может быть max, min, или не быть ни того ни другого. В этом случае исследование функции надо вести первым способом (т.е. исследовать знак первой производной).
, то в этой точке может быть max, min, или не быть ни того ни другого. В этом случае исследование функции надо вести первым способом (т.е. исследовать знак первой производной).

 Пример:
Пример:
 , где
, где  - точка max (одного из), точнее – наибольший max. Однако может случиться, что sup достигается на одном из концов отрезка.
- точка max (одного из), точнее – наибольший max. Однако может случиться, что sup достигается на одном из концов отрезка. достигает sup либо в одной из точек max, либо на концах отрезка.
достигает sup либо в одной из точек max, либо на концах отрезка.
 . Найти supr и inf на
. Найти supr и inf на 

 . Найдём многочлен
. Найдём многочлен  степени не выше n, такой, что
степени не выше n, такой, что  , а
, а  , где
, где  : Итак
: Итак
 «близок» к
«близок» к  с неопределёнными коэффициентами:
с неопределёнными коэффициентами:
 будем искать из условия (1). Предварительно найдём производные от
будем искать из условия (1). Предварительно найдём производные от 

 и заменяя
и заменяя  на
на  , согласно (1), получим:
, согласно (1), получим:
 получим
получим
 разность между
разность между 
 и тогда
и тогда  или в развёрнутом виде
или в развёрнутом виде
 , для которых
, для которых  ,
,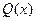 - некоторая функция, которую нужно определить. При фиксированных
- некоторая функция, которую нужно определить. При фиксированных 
 .
.




 имеет производную для
имеет производную для  , причём
, причём  и
и  . Поэтому к
. Поэтому к  , в которой
, в которой  . Отсюда и из (*) следует, что
. Отсюда и из (*) следует, что или
или и тогда
и тогда
 заключено между
заключено между  , где
, где 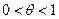 , и тогда
, и тогда  можно записать в виде:
можно записать в виде:
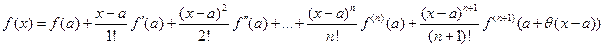 называется формулой Тейлора для
называется формулой Тейлора для  , то
, то .
.
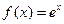 . В первую очередь найдём значения
. В первую очередь найдём значения  при
при 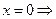

 , где
, где  , то взяв
, то взяв  , получим оценку остаточного члена
, получим оценку остаточного члена
 , получается формула, позволяющая найти приближённое значение числа
, получается формула, позволяющая найти приближённое значение числа  :
:
 или
или  .
. остаточный член
остаточный член  при
при  .
.
 . Введём обозначение
. Введём обозначение  При
При  , и т.д., можно написать
, и т.д., можно написать
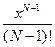 есть const, не зависящая от n, а
есть const, не зависящая от n, а  при
при 


 с любой степенью точности, взяв достаточно большое n.
с любой степенью точности, взяв достаточно большое n.

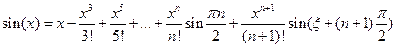 .
. .
. , положив
, положив  .
.

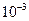 или
или  с точностью до
с точностью до  .
. .
. ,
, может быть либо max, либо min, либо нет ни того, ни другого. Покажем, как в это случае может быть использована формула Тейлора.
может быть либо max, либо min, либо нет ни того, ни другого. Покажем, как в это случае может быть использована формула Тейлора.

 непрерывна в окрестности x=a и
непрерывна в окрестности x=a и  , что при
, что при  . При этом, если
. При этом, если 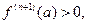 то и во всех точках интервала
то и во всех точках интервала 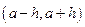 будет
будет  и если
и если  и
и  . Перепишем (2) в виде:
. Перепишем (2) в виде:
 . Тогда в интервале
. Тогда в интервале  , и т.к.
, и т.к.  . Т.к.
. Т.к. 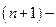 чётное число
чётное число  и правая часть (2’) <0. Следовательно,
и правая часть (2’) <0. Следовательно,  точка максимума
точка максимума  , т.к.
, т.к. 
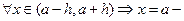 точка минимума
точка минимума  имеет разные знаки при
имеет разные знаки при  и
и  .
. -я производная сохраняет знак во всех точках
-я производная сохраняет знак во всех точках  имеет разные знаки при
имеет разные знаки при 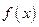 .
. , и первая не обращающаяся в 0 производная
, и первая не обращающаяся в 0 производная  есть производная чётного порядка, то в
есть производная чётного порядка, то в  .
. есть производная нечётного порядка, то
есть производная нечётного порядка, то  , найти максимум, минимум.
, найти максимум, минимум.

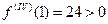 , порядок чётный и
, порядок чётный и  минимум
минимум  , если все точки кривой лежат ниже любой касательной, проведенной к любой точке из этого интервала.
, если все точки кривой лежат ниже любой касательной, проведенной к любой точке из этого интервала. , если все её точки лежат выше любой её касательной на
, если все её точки лежат выше любой её касательной на  кривая
кривая  . Проведём касательную к графику
. Проведём касательную к графику  . Теорема будет доказана, если все точки
. Теорема будет доказана, если все точки  будет меньше ординаты у касательной при одном и том же значении
будет меньше ординаты у касательной при одном и том же значении  имеет вид:
имеет вид: или
или .
. , которую можно записать в виде:
, которую можно записать в виде: .
. мы можем записать:
мы можем записать: (где С лежит между
(где С лежит между 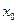 ), или
), или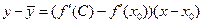 ,
,
 ,
,  между
между  и
и  . Тогда
. Тогда  ; т.к.
; т.к.  и
и  и по условию теоремы
и по условию теоремы  , т.е. Теорема 1 доказана.
, т.е. Теорема 1 доказана. , тогда
, тогда  . В этом случае
. В этом случае  и
и  , но
, но 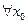
 ордината касательной больше ординаты графика
ордината касательной больше ординаты графика 
 , то кривая
, то кривая  есть
есть  - угла наклона касательной в точке с абсциссой
- угла наклона касательной в точке с абсциссой  Если
Если  убывает при возрастании
убывает при возрастании 
 возрастает при возрастании
возрастает при возрастании  - кривая выпукла.
- кривая выпукла. - кривая вогнута.
- кривая вогнута.
 , или
, или  не существует, и при переходе через
не существует, и при переходе через  есть точка перегиба.
есть точка перегиба. и
и  , тогда при
, тогда при  есть точка перегиба.
есть точка перегиба.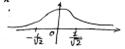

 (кривая Гаусса)
(кривая Гаусса) - нет точек перегиба
- нет точек перегиба , но при
, но при 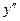 не существует.
не существует. расстояния от начала координат до этой точки) неограниченно приближается к некоторой прямой.
расстояния от начала координат до этой точки) неограниченно приближается к некоторой прямой.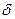 от точки
от точки  до этой прямой стремится к нулю.
до этой прямой стремится к нулю. ,
,
 . Тогда
. Тогда  ,
,  - асимптота, т.к.
- асимптота, т.к.  ,
, 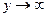 .
. - б.м. вертикальных асимптот,
- б.м. вертикальных асимптот, 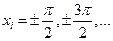 ,
, .
. .
. и
и  . Пусть
. Пусть 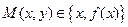 и
и  .
.  расстояние от
расстояние от 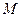 до
до  . По условию
. По условию

 - угол наклона
- угол наклона  из
из  ; т.к.
; т.к.  , то
, то .
. и (2’) приобретает вид:
и (2’) приобретает вид: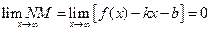 .
.
 или
или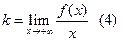

 есть асимптота,
есть асимптота, 

 - вертикальная асимптота.
- вертикальная асимптота.

 - асимптота.
- асимптота.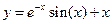 , вертикальных нет,
, вертикальных нет, 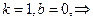
 при
при  ,
, асимптоты нет.
асимптоты нет.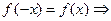 достаточно исследовать
достаточно исследовать  ОДЗ, т.к. график симметричен OY.
ОДЗ, т.к. график симметричен OY. также достаточно провести исследование для
также достаточно провести исследование для 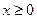 . График симметричен относительно начала координат.
. График симметричен относительно начала координат. и построить её график.
и построить её график.

 Сравним между собой 2 кривые:
Сравним между собой 2 кривые:  и
и  - имеющие в точке
- имеющие в точке  одну и ту же касательную. Пусть
одну и ту же касательную. Пусть 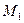 и
и  , лежащие на
, лежащие на  . С другой стороны, при одинаковом угле поворота касательной более искривлена та дуга, длина которой меньше, т.е. кривая
. С другой стороны, при одинаковом угле поворота касательной более искривлена та дуга, длина которой меньше, т.е. кривая  - средняя кривизна,
- средняя кривизна,  - угол смежности, на который поворачивается касательная при переходе от
- угол смежности, на который поворачивается касательная при переходе от  - длина дуги. Тогда
- длина дуги. Тогда .
. . Для неё
. Для неё  .
. .
. .
. только для окружности
только для окружности  и для прямой (0). Для других кривых, вероятно, кривизна – переменная величина. Она различна для дуг разной длины с общей точкой и зависит от положения на кривой.
и для прямой (0). Для других кривых, вероятно, кривизна – переменная величина. Она различна для дуг разной длины с общей точкой и зависит от положения на кривой. . За меру кривизны кривой в точке примем предел, к которому стремится средняя кривизна дуги, имеющей начало в заданной точке, когда длина
. За меру кривизны кривой в точке примем предел, к которому стремится средняя кривизна дуги, имеющей начало в заданной точке, когда длина  .
.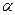 - угол касательной с ОХ. Тогда
- угол касательной с ОХ. Тогда  , а т.к.
, а т.к. 
 .
.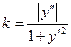 .
. - радиус кривизны.
- радиус кривизны. лежит на нормали со стороны вогнутости кривой, на расстоянии
лежит на нормали со стороны вогнутости кривой, на расстоянии  от данной точки на кривой.
от данной точки на кривой.
 .
. или
или .
.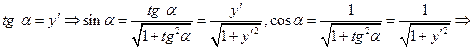
 - координаты центра кривизны.
- координаты центра кривизны. и
и  являются функциями
являются функциями  , то при изменении
, то при изменении 


