Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторная функция скалярного аргументаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
и её дифференцирование. Одним из наиболее простых способов задания пространственной кривой является задание векторного уравнения: (1) где Т.о. переменный вектор Разлагая (2) Это разложение даёт возможность перейти к параметрическому уравнению кривой: (3) Другими словами, задание векторной функции равносильно заданию трёх скалярных. По отношению к векторной функции (1), определяющему данную кривую, сама кривая называется годографом этой функции. Начало координат называют в этом случае полюсом годографа. Пусть теперь
Вектор
Векторная функция
Для нахождения производной от
Установим теперь направление Если воспользоваться разложением (*)
Отсюда деля (*) на (4) Опираясь на (4), можно показать, что справедливы следующие формулы: (5) (6) (7) (8) Доказательство (7).
Исследуем теперь некоторые свойства
Далее Т.к. мы считаем дугу годографа спрямляемой, то тогда
Т.о. модуль производной от векторной функции скалярного аргумента равен производной от дуги годографа по тому же аргументу. Следствие 1. Если
Следствие 2. Если за аргумент векторной функции принята длина дуги годографа
Т.о. производная от векторной функции по длине дуги годографа равна единичному вектору касательной к годографу, направленному в сторону увеличения длины дуги. Следствие 3. Если годограф векторной функции рассматривать как траекторию движения точки, а В самом деле, скалярная величина скорости равна производной от пути по времени:
Кроме того, вектор Т.о. Рассмотрим теперь (*) Дифференцируя (*), найдём:
В частности, производный вектор от любого переменного по направлению единичного Пусть теперь
Модуль производной от единичного переменного вектора равен угловой скорости вращения этого вектора. Как и для скалярных функций, дифференциал векторной функции записывается в виде
Но
Кривизна пространственной кривой. Сопровождающий трёхгранник. Согласно следствию 2, для
Изменение направления
С другой стороны,
Вектор Определение. Нормаль кривой, по которой направлен вектор кривизны кривой в данной точке – главная нормаль пространственной кривой. Т.о. Построим теперь третий единичный вектор
Вектор Взятые попарно
Уравнения касательной, нормали и бинормали. Уравнения плоскостей сопровождающего трехгранника. Зная Для этого в каноническом уравнении прямой
и в уравнении плоскости, проходящей через данную точку
принять за
Если кривая задана векторным уравнением (1) Для нахождения
Но, т.к.
Перемножим теперь векторно (*) На основании (*) за вектор
Но тогда, за
Т.о. в любой точке произвольной кривой мы можем определить все элементы сопроводдающего трехгранника. Пример. Уравнение касательной, нормали и бинормали к правой винтовой линии в любой точке.
Касательная Главнвя нормаль Бинормаль
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 589; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.116.77 (0.007 с.) |

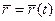 ,
, - радиус-вектор точки кривой, а
- радиус-вектор точки кривой, а 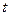 - параметр, определяющий положение точки.
- параметр, определяющий положение точки. есть функция скаляра
есть функция скаляра 

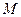 и
и 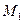 - точки кривой, определяемой уравнением (1). Причём
- точки кривой, определяемой уравнением (1). Причём  , а
, а 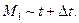 Радиус-векторы этих точек будут
Радиус-векторы этих точек будут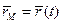 и
и 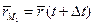 .
. называют приращением векторной функции
называют приращением векторной функции 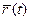 , соответствующее приращению
, соответствующее приращению  её аргумента, и обозначают через
её аргумента, и обозначают через 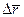 ,
,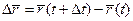 .
. .
.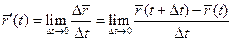 .
.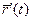 . Очевидно, что
. Очевидно, что  коллинеарен с
коллинеарен с 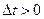 направлен в ту же сторону, что и
направлен в ту же сторону, что и  а при
а при 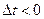 - в противоположную сторону. Но в первом случае
- в противоположную сторону. Но в первом случае  а во втором
а во втором 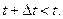 Т.о. вектор
Т.о. вектор  по ортам, то
по ортам, то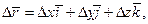 где
где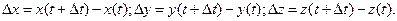
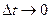 для
для 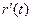 получим
получим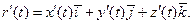

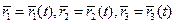
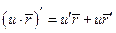
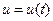 - скалярная функция.
- скалярная функция.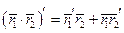
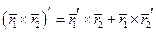
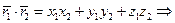
 Ч.Т.Д.
Ч.Т.Д.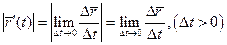 .
.
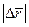 - есть длина хорды, а
- есть длина хорды, а  - длина дуги. Поэтому
- длина дуги. Поэтому
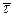 - единичный вектор, направленный по касательной к годографу в сторону увеличения
- единичный вектор, направленный по касательной к годографу в сторону увеличения 
 , то
, то (т.к.
(т.к. 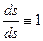 )
)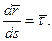
 , то
, то 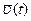 .
.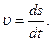
 направлен по касательной к траектории в сторону движения, что соответствует направлению возрастания
направлен по касательной к траектории в сторону движения, что соответствует направлению возрастания  .
. , т.е.
, т.е. где
где 
 , т.е.
, т.е. 
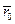 всегда
всегда  .
. угол между радиусами единичной сферы, проведёнными в точки
угол между радиусами единичной сферы, проведёнными в точки 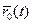 . Тогда длина хорды
. Тогда длина хорды 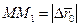 из треугольника
из треугольника 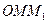 будет равна
будет равна
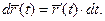
 и тогда
и тогда
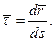
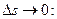

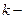 кривизна,
кривизна,  длина дуги.
длина дуги.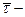 единичный вектор и производный к нему вектор
единичный вектор и производный к нему вектор 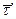 перпендикулярен к нему, а его модуль
перпендикулярен к нему, а его модуль  Дифференцируя
Дифференцируя 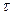 по
по 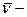 единичный вектор с направлением
единичный вектор с направлением 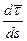 , найдём:
, найдём:
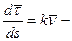 вектор кривизны пространственной кривой. Его направление, перпендикулярное к направлению касательной, является направлением нормали пространственной кривой. Но пространственная кривая имеет в любой точке бесчисленное множество нормалей, которые все лежат в плоскости, проходящей через данную точку кривой и перпендикулярно к касательной в данной точке. Эту плоскость называют нормальной плоскостью пространственной кривой.
вектор кривизны пространственной кривой. Его направление, перпендикулярное к направлению касательной, является направлением нормали пространственной кривой. Но пространственная кривая имеет в любой точке бесчисленное множество нормалей, которые все лежат в плоскости, проходящей через данную точку кривой и перпендикулярно к касательной в данной точке. Эту плоскость называют нормальной плоскостью пространственной кривой. равный векторному произведению
равный векторному произведению 

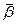 , как и
, как и 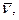 также перпендикулярен
также перпендикулярен 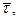 т.е. лежит в нормальной плоскости. Его направление называют направлением бинормали пространственной кривой в данной точке. Вектора
т.е. лежит в нормальной плоскости. Его направление называют направлением бинормали пространственной кривой в данной точке. Вектора  и
и 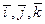 в правой системе координат.
в правой системе координат. определяют три плоскости, проходящие через одну и ту же точку на кривой и образуют грани сопровождающего трехгранника. При этом
определяют три плоскости, проходящие через одну и ту же точку на кривой и образуют грани сопровождающего трехгранника. При этом 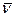 определяют соприкасающую плоскость (б.м. дуга кривой в окрестности данной точки есть дуга плоской кривой в соприкасаемой плоскости с точностью до б.м. высшего порядка);
определяют соприкасающую плоскость (б.м. дуга кривой в окрестности данной точки есть дуга плоской кривой в соприкасаемой плоскости с точностью до б.м. высшего порядка); и
и 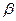 , или любые коллинеарные им неединичные вектора T, N и B выведем уравнения, поименованные в этом параграфе.
, или любые коллинеарные им неединичные вектора T, N и B выведем уравнения, поименованные в этом параграфе.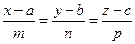
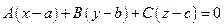
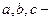 координаты выбранной на кривой точки, за
координаты выбранной на кривой точки, за  или соответственно за
или соответственно за 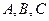 принять координаты того из векторов
принять координаты того из векторов  или
или  , который определяет направление искомой прямой или нормали к искомой плоскости:
, который определяет направление искомой прямой или нормали к искомой плоскости: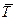 - для касательной или нормальной плоскости,
- для касательной или нормальной плоскости,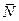 - для главной нормали и спрямляющей плоскости,
- для главной нормали и спрямляющей плоскости, - для бинормали и соприкасающейся плоскости.
- для бинормали и соприкасающейся плоскости.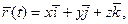 то за вектор
то за вектор  направленный по касательной можно принять
направленный по касательной можно принять 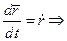
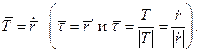
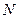 и
и 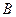 найдём сначала разложение
найдём сначала разложение  по векторам
по векторам 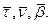 Ранее (следствие 1) мы нашли, что
Ранее (следствие 1) мы нашли, что  Дифференцируя по
Дифференцируя по 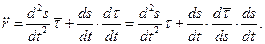


 и
и 
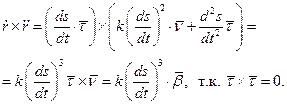

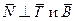 можно принять векторное произведение этих последних:
можно принять векторное произведение этих последних: