
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наибольшее и наименьшее значения функции на отрезке.Содержание книги
Поиск на нашем сайте Пусть Предположим, что Итак, То же самое можно сказать и о наименьшем значении Итак, если требуется найти наибольшее (наименьшее) значение непрерывной 1) Найти все max (min) 2) Вычислить значения 3) Из всех полученных выше значений выбрать наибольшее (наименьшее). Пример.
Формула Тейлора Предположим, что (1) Естественно предположить, то Будем искать (2)
(3) Подставляя теперь вместо
Подставляя теперь вместо (5) Обозначим теперь через
(6)
Т.о. (6) даёт возможность заменить Следующая задача – оценить
где Рассмотрим далее вспомогательную функцию от
Далее найдём
После сокращения получим (*) Итак,
остаточный член в форме Лагранжа. Т.к.
Формула
Если в формуле Тейлора положить (**) Этот частный случай формулы Тейлора называют формулой Маклорена.
Разложение по формуле Тейлора функций 1.
Подставляя эти значения в формулу (**) Маклорена, получим
Если
При
Здесь ошибка не превосходит Отметим, что для Действительно
Т.к.
Но
Следовательно, и Т.о. для 2.
Подставляя теперь эти значения в формулу Тейлора, получим
Т. к Применим полученную формулу для
Оценим теперь остаточный член:
Следовательно, ошибка меньше чем 3.
(х – в радианах).
Исследование функции на максимум и минимум С помощью формулы Тейлора. Ранее мы показали, что если при Предположим, что при x=a (1) Пусть также f(x) имеет непрерывные производные до (n+1) -го порядка включительно в окрестности x=a. Запишем для f(x) формулу Тейлора, учитывая (1): (2) Т.к. (2’) и рассмотрим различные возможные случаи. 1. n – нечётное а) б) 2. n – чётное Тогда n+1 – нечётное, и Если h достаточно мало по модулю, то Таким образом, если при
Если же
Пример. 1) Критические точки
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 508; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

 непрерывна на [ a, b ]. Тогда она достигает на нём своего наибольшего и наименьшего значений.
непрерывна на [ a, b ]. Тогда она достигает на нём своего наибольшего и наименьшего значений. имеет на [ a, b ] конечное число критических точек. Если
имеет на [ a, b ] конечное число критических точек. Если  , где
, где  - точка max (одного из), точнее – наибольший max. Однако может случиться, что sup достигается на одном из концов отрезка.
- точка max (одного из), точнее – наибольший max. Однако может случиться, что sup достигается на одном из концов отрезка. достигает sup либо в одной из точек max, либо на концах отрезка.
достигает sup либо в одной из точек max, либо на концах отрезка.
 . Найти supr и inf на
. Найти supr и inf на 

 . Найдём многочлен
. Найдём многочлен  степени не выше n, такой, что
степени не выше n, такой, что  , а
, а  , где
, где  : Итак
: Итак
 «близок» к
«близок» к  с неопределёнными коэффициентами:
с неопределёнными коэффициентами:
 будем искать из условия (1). Предварительно найдём производные от
будем искать из условия (1). Предварительно найдём производные от 

 и заменяя
и заменяя  на
на  , согласно (1), получим:
, согласно (1), получим:
 получим
получим
 разность между
разность между 
 и тогда
и тогда  или в развёрнутом виде
или в развёрнутом виде
 , для которых
, для которых  ,
,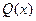 - некоторая функция, которую нужно определить. При фиксированных
- некоторая функция, которую нужно определить. При фиксированных 
 .
.




 имеет производную для
имеет производную для  , причём
, причём  и
и  . Поэтому к
. Поэтому к  , в которой
, в которой  . Отсюда и из (*) следует, что
. Отсюда и из (*) следует, что или
или и тогда
и тогда
 заключено между
заключено между  , где
, где 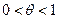 , и тогда
, и тогда  можно записать в виде:
можно записать в виде:
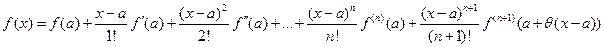 называется формулой Тейлора для
называется формулой Тейлора для  , то
, то .
.
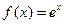 . В первую очередь найдём значения
. В первую очередь найдём значения  при
при 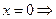

 , где
, где  , то взяв
, то взяв  , получим оценку остаточного члена
, получим оценку остаточного члена
 , получается формула, позволяющая найти приближённое значение числа
, получается формула, позволяющая найти приближённое значение числа  :
:
 или
или  .
. остаточный член
остаточный член  при
при  .
.
 . Введём обозначение
. Введём обозначение  При
При  , и т.д., можно написать
, и т.д., можно написать
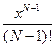 есть const, не зависящая от n, а
есть const, не зависящая от n, а  при
при 


 с любой степенью точности, взяв достаточно большое n.
с любой степенью точности, взяв достаточно большое n.

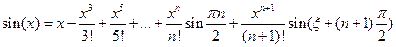 .
. .
. , положив
, положив  .
.

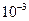 или
или  с точностью до
с точностью до  .
. .
. ,
, может быть либо max, либо min, либо нет ни того, ни другого. Покажем, как в это случае может быть использована формула Тейлора.
может быть либо max, либо min, либо нет ни того, ни другого. Покажем, как в это случае может быть использована формула Тейлора.

 непрерывна в окрестности x=a и
непрерывна в окрестности x=a и  , что при
, что при  . При этом, если
. При этом, если 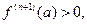 то и во всех точках интервала
то и во всех точках интервала 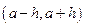 будет
будет  и если
и если  и
и  . Перепишем (2) в виде:
. Перепишем (2) в виде:
 . Тогда в интервале
. Тогда в интервале  , и т.к.
, и т.к.  . Т.к.
. Т.к. 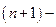 чётное число
чётное число  и правая часть (2’) <0. Следовательно,
и правая часть (2’) <0. Следовательно,  точка максимума
точка максимума  , т.к.
, т.к. 
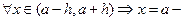 точка минимума
точка минимума  имеет разные знаки при
имеет разные знаки при  и
и  .
. -я производная сохраняет знак во всех точках
-я производная сохраняет знак во всех точках  имеет разные знаки при
имеет разные знаки при 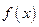 .
. , и первая не обращающаяся в 0 производная
, и первая не обращающаяся в 0 производная  есть производная чётного порядка, то в
есть производная чётного порядка, то в  .
. есть производная нечётного порядка, то
есть производная нечётного порядка, то  , найти максимум, минимум.
, найти максимум, минимум.

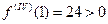 , порядок чётный и
, порядок чётный и  минимум
минимум 


