
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование кривых, заданных параметрами.Содержание книги Поиск на нашем сайте
Пусть 1) Вычисляем
2) Для точек кривой, вблизи которых кривая является графиком некоторой функции
3) Находим 4) Далее находим
и исследуя на знак, определяем направления выпуклости кривой на любом интервале. Для нахождения асимптот находим такие Затем исследование проводится обычным способом. Другие особенности поясним на примерах. Пример.
Далее (*) (**) На основании (*) и (**) составим таблицу:
Из таблицы следует, что (1) определяет 2 непрерывных Из (**) следует, что
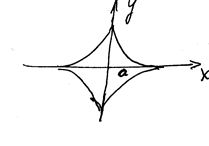
(астроида)
Элементы дифференциальной геометрии. Касательная и нормаль к плоской кривой. Как было показано раньше, уравнение касательной к кривой
где Определение. Прямая, проходящая через точку касания перпендикулярно к касательной, называется нормалью к кривой Используя условие перпендикулярности двух прямых, нетрудно вывести уравнение нормали:
Пример 1. Найти уравнение касательной и нормали к Дифференцируя, получим Уравнение касательной т.к. Уравнение нормали
Пример 2. Касательная и нормаль к циклоиде:
Касательная и нормаль в точке
Касательная и нормаль кривой, проведённые в
Все эти отрезки лкгко могут быть вычислены через
Поэтому:
Знаки модуля введены потому, что Пример. Доказать, что
2.
Дифференциал дуги плоской и пространственной кривой. Определение. Кривые, для которых может быть установлено понятие длины, называются спрямляемыми. Условие спрямляемости для плоской кривой, заданной
Опираясь на это свойство найдём выражение для дифференциала дуги кривой. На плоской кривой
т.к.
и т.к.
Если кривая задана
Если же кривая задана уравнением в полярных координатах
Примеры. Найти Ответ: Дифференциал дуги пространственной кривой находится аналогично. Отличие состоит в том, что длина хорды
Пример. Винтовая линия: Формулам для
которые легко получить из предыдущих внося
Дифференциал дуги кривой имеет простой геометрический смысл: он равен длине отрезка касательной от точки касания до точки с абсциссой
Кривизна плоской кривой.
Т.о. можно принять, что мера кривизны конечного участка гладкой (дифференцируемой) кривой должна быть прямо пропорциональна углу, на который поворачивается касательная при переходе от начальной точки дуги к конечной и обратно пропорциональна длине этой дуги. Поэтому, за меру кривизны конечной дуги (средняя кривизна) можно принять отношение угла поворота касательной к длине дуги. Пусть
Применим это определение к окружности радиуса
Т.к. длина дуги Т.о. кривизна любой дуги окружности есть const Вывод естественный: любая дуга при перемещении её по окружности всеми точками будет лежать на окружности. При этом с уменьшением R кривизна будет возрастать. Для кривых Поэтому, естественно от понятия средней кривизны на данном участке перейти к понятию кривизны кривой в данной точке, совершая предельный переход при
Определение. Кривизна кривой в точке есть производная от угла поворота касательной к кривой по длине дуги. При этом угол поворота касательной можно измерять разностью углов касательных с осью, например, Х. Выводим теперь формулу для вычисления кривизны кривой
Если не учитывать направление вогнутости кривой, то
Построим теперь окружность, которая имеет общую касательную с кривой в точке, общую кривизну и направление выгнутости. Такую окружность окружностью кривизны, её радиус – радиусом кривизны, а её центр – центром кривизны. Т.к. кривизна окружности обратна её R, то для радиуса кривизны получим (*) Центр кривизны
Рисунок соответствует случаю
Но (**) Т.к. Определение. Геометрическое место центров кривизны кривой Пользуясь уравнениями (**) следующие свойства эволюты: 1. Касательная к эволюте в некоторой её точке служит соответствующая этой точке нормаль эвольвенты. 2. Дифференциал дуги эволюты равен дифференциалу радиуса кривизны эвольвенты.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 601; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.2.6 (0.011 с.) |

 , исследуем аналогично
, исследуем аналогично  .
. и
и  .
. , вычисляем
, вычисляем .
. , при которых хотя бы одна из
, при которых хотя бы одна из  или
или  обращается в нуль или терпит разрыв, следовательно,
обращается в нуль или терпит разрыв, следовательно,  , (а следовательно, и в любом
, (а следовательно, и в любом  ) определяем знак
) определяем знак  и тем самым находим области возрастания и убывания
и тем самым находим области возрастания и убывания 
 , что при
, что при  или
или  или
или 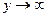 , или и
, или и  (1’)
(1’) и
и 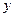 опр. для
опр. для  , но в силу периодичности
, но в силу периодичности  . Тогда
. Тогда  и
и 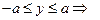 кривая асимптот не имеет.
кривая асимптот не имеет. при
при 









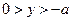




 и при
и при  .
. и
и  , т.е. в этих точках касательная к
, т.е. в этих точках касательная к 
 , т.е. касательная к
, т.е. касательная к  :
:
 при
при  - кривая вогнутая,
- кривая вогнутая, при
при  - кривая выпуклая.
- кривая выпуклая. , которая называется точкой касания, имеет вид:
, которая называется точкой касания, имеет вид: ,
,
 или
или .
. в точке
в точке 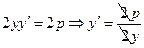 и
и  .
. или
или  ,
, .
.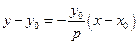 или
или .
.

 будут иметь уравнения:
будут иметь уравнения: - касательная
- касательная - нормаль
- нормаль , в пересечении с OX образуют
, в пересечении с OX образуют  . Катеты этого треугольника -
. Катеты этого треугольника - 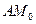 и
и  , отрезки
, отрезки  и
и  , на которые ордината
, на которые ордината  делит гипотенузу
делит гипотенузу  , часто используют в различных вопросах геометрии и получили специальные обозначения и названия:
, часто используют в различных вопросах геометрии и получили специальные обозначения и названия:
 - длина касательной,
- длина касательной, - длина нормали,
- длина нормали, - подкасательная,
- подкасательная, - поднормаль.
- поднормаль. в точке
в точке  .
. или
или 




 - поднормаль
- поднормаль 
 имеет подкасательную -
имеет подкасательную -  .
.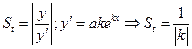 .
. и
и  должны иметь непрерывные производные по t -
должны иметь непрерывные производные по t -  и
и  . Аналогично записывается условие спрямляемости и пространственной кривой: непрерывность
. Аналогично записывается условие спрямляемости и пространственной кривой: непрерывность 
 Для всякой спрямляемой кривой справедливо геометрическое свойство: предел отношения б.м. дуги кривой к стягивающей её хорде равен 1, при условии, что хорда стягивается в точку. Если длину
Для всякой спрямляемой кривой справедливо геометрическое свойство: предел отношения б.м. дуги кривой к стягивающей её хорде равен 1, при условии, что хорда стягивается в точку. Если длину  , а хорды -
, а хорды - 
 .
. которые соответствуют
которые соответствуют 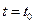 и
и  . Длина хорды
. Длина хорды  . Найдём теперь производную от длины дуги
. Найдём теперь производную от длины дуги  по
по 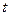 :
: ,
, при
при 



 ,
,  получим
получим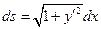 .
. , то за параметр можно принять угол
, то за параметр можно принять угол  , и тогда
, и тогда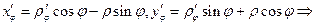

 .
. для циклоиды
для циклоиды  .
.
 , соединяющей
, соединяющей  и
и  определяется формулой:
определяется формулой:

 .
.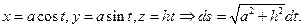
 или
или  ,
, под знак корня и заменяя
под знак корня и заменяя .
. .
.
 Сравним между собой 2 кривые:
Сравним между собой 2 кривые:  и
и  - имеющие в точке
- имеющие в точке 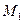 и
и  , лежащие на
, лежащие на  . С другой стороны, при одинаковом угле поворота касательной более искривлена та дуга, длина которой меньше, т.е. кривая
. С другой стороны, при одинаковом угле поворота касательной более искривлена та дуга, длина которой меньше, т.е. кривая  - средняя кривизна,
- средняя кривизна,  - угол смежности, на который поворачивается касательная при переходе от
- угол смежности, на который поворачивается касательная при переходе от  - длина дуги. Тогда
- длина дуги. Тогда .
. . Для неё
. Для неё  .
. .
. .
. только для окружности
только для окружности  и для прямой (0). Для других кривых, вероятно, кривизна – переменная величина. Она различна для дуг разной длины с общей точкой и зависит от положения на кривой.
и для прямой (0). Для других кривых, вероятно, кривизна – переменная величина. Она различна для дуг разной длины с общей точкой и зависит от положения на кривой. . За меру кривизны кривой в точке примем предел, к которому стремится средняя кривизна дуги, имеющей начало в заданной точке, когда длина
. За меру кривизны кривой в точке примем предел, к которому стремится средняя кривизна дуги, имеющей начало в заданной точке, когда длина  .
.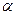 - угол касательной с ОХ. Тогда
- угол касательной с ОХ. Тогда  , а т.к.
, а т.к. 
 .
.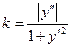 .
. - радиус кривизны.
- радиус кривизны. лежит на нормали со стороны вогнутости кривой, на расстоянии
лежит на нормали со стороны вогнутости кривой, на расстоянии  от данной точки на кривой.
от данной точки на кривой.
 .
. или
или .
.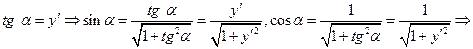
 - координаты центра кривизны.
- координаты центра кривизны. и
и  являются функциями
являются функциями  , то при изменении
, то при изменении 


