
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближённое решение уравнений.Содержание книги Поиск на нашем сайте
Интерполирование функций.
Действительные корни Пусть дано уравнение Графический способ. Приведём
 После этого строятся графики После этого строятся графики  и и  на одной координатной плоскости. Абсциссы точек пересечения этих кривых будут корнями уравнения на одной координатной плоскости. Абсциссы точек пересечения этих кривых будут корнями уравнения  а следовательно, и а следовательно, и  т.к. в общей точке т.к. в общей точке  и и 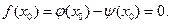 Отсутствие общих точек означает отсутствие действительных корней Отсутствие общих точек означает отсутствие действительных корней  Т.о. это построение даёт возможность определить число действительных корней и их приближённые числовые значения. Т.о. это построение даёт возможность определить число действительных корней и их приближённые числовые значения.
В случае (1) мы имеем 2 действительных корня На рис.1 видно, что Приближённое значение Приближённое значение Т.о. отделены оба действительных корня Построенные прмежутки можно «сужать» и тогда новые отрезки (границы) будут давать всё более точные приближённые значения корней. Метод деления отрезка пополам.
Методы уточнения приближённого корня.
Т.к.
а по формуле Лагранжа
где
Следовательно,
которое находится между
где Теорема. Последовательность
Доказательство. Т.к.
Метод уточнения корня с помощью формулы (*) называют методом Ньютона. Итак метод Ньютона применим, если в промежутке Эти условия являются достаточными. Т.е. рпи их нарушении может случиться так, что корень всё же находится по методу Ньютона. Оценим теперь абсолютную погрешность
где По формуле Лагранжа
но
Т.к. Если Метод хорд. Пусть Уравнение хорды
Вычислим теперь Абсолютная погрешность
где По формуле Лагранжа имеем
но
Метод итерации. Пусть (*) Пусть (А) Геометрически эти требования значат, что график Приводя
будет абсцисса точки Приведение Если условие (А) соблюдается, то метод итераций позволяет вычислить корень Метод итераций заключается в следующем: (*) Теорема. Если Доказательство. Пусть окрестность
Т.к.
т.е.
Теперь заметим, что
или
Рассмотрим теперь
Абсолютная погрешность
Действительно
Проверку абсолютной погрешности целесообразно проводить на любом шаге вычислений, если заранее известна величина Комбинированный способ уточнения корня. Суть метода заключается в одновременном применении метода хорд и метода касательных на отрезке
|
|||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.209.20 (0.009 с.) |

 .
. дифференцируемая функция. Требуется найти все действительные корни с заданной точностью.
дифференцируемая функция. Требуется найти все действительные корни с заданной точностью. Оба эти уравнения равносильны, т.е. имеют одни и те же корни. Распределение членов выполняется с учётом простоты построения графиков
Оба эти уравнения равносильны, т.е. имеют одни и те же корни. Распределение членов выполняется с учётом простоты построения графиков  и
и  . Например:
. Например:  где
где  и
и  Для
Для 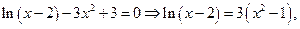 где
где  и
и 

 и
и 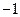 , в (2) – нет. Зная теперь приближённые значения корней (1) «отделим» точные корни, т.е. построим тесные числовые промежутки
, в (2) – нет. Зная теперь приближённые значения корней (1) «отделим» точные корни, т.е. построим тесные числовые промежутки  в каждом из которых содержится только один точный корень
в каждом из которых содержится только один точный корень  изменяет знак в любом корне. На самом деле это не всегда так, но…
изменяет знак в любом корне. На самом деле это не всегда так, но…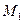 с «+» на «-», а в
с «+» на «-», а в  - с «-» на «+».
- с «-» на «+». но
но 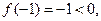 значит точное значение
значит точное значение  Возьмём, например,
Возьмём, например,  тогда
тогда  тогда в промежутке
тогда в промежутке 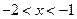
 Говорят, что
Говорят, что  «отделён» с помощью этого промежутка.
«отделён» с помощью этого промежутка. но
но  следовательно,
следовательно,  Но при
Но при 
 в
в  есть точный, единственный корень
есть точный, единственный корень 
 Числа –2 и –1 – приближённые значения
Числа –2 и –1 – приближённые значения  - по недостатку и избытку соответственно, а 0 и 1 – приближённые значения
- по недостатку и избытку соответственно, а 0 и 1 – приближённые значения 
 Метод Ньютона (касательных). Пусть
Метод Ньютона (касательных). Пусть  , отделённый промежутком
, отделённый промежутком  и пусть
и пусть  . Рассмотрим график
. Рассмотрим график  касательную
касательную  имеющую уравнение
имеющую уравнение  Эта касательная пересечёт ОХ в точке с абсциссой
Эта касательная пересечёт ОХ в точке с абсциссой  Докажем, что
Докажем, что  если
если 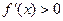 и
и  т.е. вогнута. При этих условиях, учитывая, что
т.е. вогнута. При этих условиях, учитывая, что 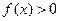 на
на  получим
получим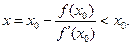
 также возрастает. Из
также возрастает. Из  имеем
имеем

 а
а  Т.к.
Т.к.  т.е.
т.е. или
или  Ч.Т.Д.
Ч.Т.Д. и поэтому
и поэтому  более точное приближение
более точное приближение  Заменяя
Заменяя 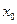 на
на 
 и
и  Продолжая процесс, получим последовательность
Продолжая процесс, получим последовательность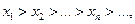
 (*)
(*) имеет пределом точный корень
имеет пределом точный корень 
 монотонно убывающая, то
монотонно убывающая, то  для
для 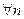 и имеет предел
и имеет предел  Покажем, что
Покажем, что 
 т.е. С – есть корень
т.е. С – есть корень  единственный корень в
единственный корень в 

 и
и  Кроме того, график
Кроме того, график  При этих условиях гарантируется существование области
При этих условиях гарантируется существование области  , которая распологается слева или справа от
, которая распологается слева или справа от 
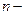 го приближения
го приближения 

 конец отрезка
конец отрезка  который не принадлежит области
который не принадлежит области 

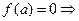

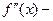 знакопостоянна, то
знакопостоянна, то  монотонно врзрастает или убывает и во всех случаях
монотонно врзрастает или убывает и во всех случаях  имеет наименьшее значение в
имеет наименьшее значение в  Поэтому, заменяя
Поэтому, заменяя  на
на  и получаем равенство (*).
и получаем равенство (*). и
и  Если построить хорду
Если построить хорду  , то абсцисса
, то абсцисса 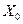 .
. полагая
полагая  получим
получим или
или где
где 
 и из двух отрезков
и из двух отрезков 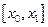 и
и  выберем тот, на концах которого
выберем тот, на концах которого  Продолжая процесс, получим последовательность
Продолжая процесс, получим последовательность  при
при 

 наименьшее значение
наименьшее значение 
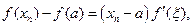 где
где 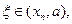
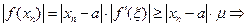


 Разрешим
Разрешим 
 и
и где
где 
 и притом должен располагаться более «полого» чем биссектриса 1-го координатного угла
и притом должен располагаться более «полого» чем биссектриса 1-го координатного угла  (если
(если  если
если  к виду
к виду  т.е. корнем
т.е. корнем
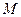 , пересечения графика
, пересечения графика 
 :
:  и т.д. Однако нужны только те преобразования, при которых выполняется (А). Подходящий вид находится методом проб. Так для
и т.д. Однако нужны только те преобразования, при которых выполняется (А). Подходящий вид находится методом проб. Так для  вид
вид  является неподходящим, т.к.
является неподходящим, т.к.  а вид
а вид  - не удовлетворяет (А), т.к.
- не удовлетворяет (А), т.к.  для
для 


 знакопостоянна на
знакопостоянна на  то последовательность (*) при
то последовательность (*) при  имеет своим пределом точный корень
имеет своим пределом точный корень 
 Составим разности между членами
Составим разности между членами 
 где
где 
 т.е.
т.е. 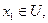 причём
причём 
 ещё ближе к
ещё ближе к  чем
чем 
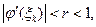 т.к. все
т.к. все  Поэтому
Поэтому

 т.к.
т.к. 
 Ч.Т.Д.
Ч.Т.Д.
 и колеблется около
и колеблется около 
 где
где 




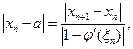 но
но 


 !
! методы хорд и касательных дают приближения по разные стороны от точного значения. Поэтому после любого шага мы получаем корень с избытком и с недостатком и эти значения могут быть использованы в качестве новых приближений или
методы хорд и касательных дают приближения по разные стороны от точного значения. Поэтому после любого шага мы получаем корень с избытком и с недостатком и эти значения могут быть использованы в качестве новых приближений или  и
и  дающих новый отрезок выделения.
дающих новый отрезок выделения.


