
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вертикальні асимптоти існують тоді, коли функціяСодержание книги
Поиск на нашем сайте
Вища математика 12-13 F(x) називається первісною для функції f(x) на проміжку (a,b), якщо на цьому проміжку: * dF(x)=f(x)dx Алгебраїчна сума скінченого числа нескінченно малих величин є величина: * нескінченно мала Алгебраїчна сума скінченої кількості доданків функцій неперервних в точці * Неперервна функція при Будь-яке рівняння першого степеня відносно * площину В усіх точках проміжку (а,b) для функції y=f(x) її друга похідна f''(x)>0. Який графік функції на цьому проміжку? * вгнутий В усіх точках проміжку (а,b) для функції y=f(x) її друга похідна f''(x)<0. Який графік функції є? * опуклий В яких випадках виконується рівність для матриць А ∙ В = В ∙ А обов’язково: * якщо А або В, або А і В одиничні матриці Вектор з координатами * Вектори задані координатами * Вектори на площині будуть перпендикулярні, якщо: *їх скалярний добуток дорівнює нулю Векторний добуток *перпендикулярний до Векторний добуток двох векторів * Векторний добуток одиничних векторів * Векторний добуток ортів ̃ * Величина * Вертикальні асимптоти існують тоді, коли функція * Має розрив другого роду Вибрати з понять те, яке відповідає поняттю числового ряду * Числова послідовність Визначити розбіжність або збіжність ряду *ряд розбіжний Визначити одиничну матрицю розміром 2x2. * Визначити, парна, чи непарна функція *Функція не є ні парною, ні непарною Визначний інтеграл * певне число Визначник матриці А дорівнює нулю, це означає *матриця А не має оберненої матриці Визначником другого порядку, що відповідає даній матриці, називається число * Вкажіть позначення границі послідовності * Вкажіть правильну відповідь * Вкажіть правильну відповідь * будь яка стала Вкажіть правильну відповідь для інтеграла * Вкажіть рівність, яка виконується для векторного добутку двох векторів * Вкажіть рівняння прямої, що проходить через дві задані точки * Вкажіть рівняння прямої, що проходить через точку з координатами (2, 4)
* Вкажіть рівняння прямої, яка паралельна осі у * Вкажіть, чому дорівнює визначений інтеграл з однаковими межами інтегрування? * нулю Вкажіть, чому дорівнює диференціал від невизначеного інтеграла? * підінтегральній функції Вкажіть, чому дорівнює інтеграл від диференціала * F(x) + с Вкажіть, чому дорівнює похідна від невизначеного інтеграла ( * f(x) Вказати обернену матрицю до одиничної матриці Е; * Вказати рівняння лінії, яка утворює з віссю х кут * Вказати рівняння лінії, яка утворює кут * Вказати рівняння прямої, яка проходить через точку А (2, -1) і паралельна осі у * х = 2 Вказати формулу відстані від точки * Вказати формулу відстані між двома точками * Всі елементарні функції неперервні в інтервалах: * Своєї визначеності Геометричний зміст k в рівнянні прямої y=kx+b означає? *тангенс кута, утвореного прямою з додатнім напрямком осі ОХ Геометрично похідна функції * Кутовий коефіцієнт дотичної до графіка функції Геометричною прогресією є ряд виду *g<1 Границя відношення двох неперервних функцій, які мають похідні в усіх * границі відношення їх похідних при Два вектори вважаються рівними, якщо *напрями збігаються, а модулі рівні Два вектори, які лежать в одній площині або в паралельних площинах, називаються *компланарними Два вектори, які лежать на одній прямій, називаються *колінеарними Дві будь-які первісні для однієї і тієї самої функції відрізняються між собою * Відрізняються на сталу величину Дві прямі задані загальним рівнянням. При якій умові вони будуть паралельні? * Диференціальне рівняння з відокремленими змінними можна записати у вигляді * Диференціальне рівняння називається звичайним, якщо: * рівняння залежить тільки від одного аргументу Похідна функції дорівнює * Похідною функції y=f(x) за аргументом x називається * границя відношення приросту функції до приросту аргументу, коли останній прямує до нуля
При переході через точку * в точці Вища математика 12-13 F(x) називається первісною для функції f(x) на проміжку (a,b), якщо на цьому проміжку: * dF(x)=f(x)dx Алгебраїчна сума скінченого числа нескінченно малих величин є величина: * нескінченно мала Алгебраїчна сума скінченої кількості доданків функцій неперервних в точці * Неперервна функція при Будь-яке рівняння першого степеня відносно * площину В усіх точках проміжку (а,b) для функції y=f(x) її друга похідна f''(x)>0. Який графік функції на цьому проміжку? * вгнутий В усіх точках проміжку (а,b) для функції y=f(x) її друга похідна f''(x)<0. Який графік функції є? * опуклий В яких випадках виконується рівність для матриць А ∙ В = В ∙ А обов’язково: * якщо А або В, або А і В одиничні матриці Вектор з координатами * Вектори задані координатами * Вектори на площині будуть перпендикулярні, якщо: *їх скалярний добуток дорівнює нулю Векторний добуток *перпендикулярний до Векторний добуток двох векторів * Векторний добуток одиничних векторів * Векторний добуток ортів ̃ * Величина * Вертикальні асимптоти існують тоді, коли функція * Має розрив другого роду
|
||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.209.122 (0.01 с.) |

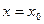 є
є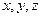 визначає
визначає називається градієнтом функції
називається градієнтом функції  і записується
і записується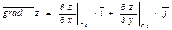
 ,
, 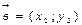 , будуть колінеарні якщо:
, будуть колінеарні якщо: ;
; 
 ∙
∙  двох векторів є вектор
двох векторів є вектор 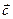 . Чому він дорівнює?
. Чому він дорівнює?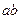 дорівнює:
дорівнює: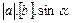
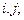

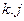 дорівнює відповідно
дорівнює відповідно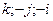
 самих на себе дорівнює
самих на себе дорівнює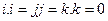
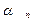 називається нескінченно малою, якщо
називається нескінченно малою, якщо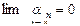
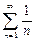 :
:

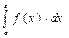 є
є
 :
:


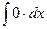 ?
?
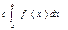
 ,
,  :
: =-
=- 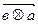
 і
і 
 .
.
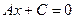
 ?
?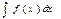 )'?
)'?
 і проходить через точку А = (-5, 5)
і проходить через точку А = (-5, 5)
 і проходить через точку А (2,-2).
і проходить через точку А (2,-2).
 до прямої, що задана загальним рівнянням:
до прямої, що задана загальним рівнянням:
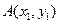 і
і 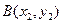 на площині:
на площині:
 означає
означає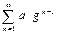 . Яка умова збіжності цього ряду? (Тут
. Яка умова збіжності цього ряду? (Тут 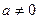 ; g - - знаменник прогресії).
; g - - знаменник прогресії). , але при x=a похідні дорівнюють нулю, дорівнює
, але при x=a похідні дорівнюють нулю, дорівнює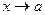
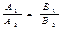
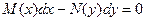

 зліва направо похідна функції знак не міняє, то точка
зліва направо похідна функції знак не міняє, то точка 


