
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Запишіть загальне рівняння прямої на площиніСодержание книги Поиск на нашем сайте
* Запишіть загальний член ряду, якщо ряд задано першими трьома членами: * Запишіть загальний член ряду: *Un = Запишіть канонічне рівняння гіперболи: * Запишіть канонічне рівняння еліпса: * Запишіть правильну відповідь * Запишіть правильну відповідь виразу * Запишіть правильну відповідь для границі * Запишіть рівняння прямої, що паралельна осі х і проходить через точку А = (-3, 2) * Збіжний чи розбіжний ряд *ряд буде розбіжним Зміст визначеного інтеграла геометрично полягає в тому, що якщо f(x) ≥0, то він дорівнює * площі відповідної криволінійної трапеції Знайдіть загальне рівняння прямої, яка проходить через початок координат * Знайдіть правильну відповідь для скалярного добутку двох векторів * Знайдіть правильну відповідь до виразу * Знайдіть рівняння прямої, яка паралельна осі х: * Знакопочерговий ряд збігається. Його сума за абсолютною величиною буде: * Знаходження первісних F(x) для функції f(x) називається * інтегруванняфункції f(x) Знаходження похідної функції y=f(x) називається * диференціюванням цієї функції Значення аргументу х, при яких функціональний ряд збігається називаються: *областю збіжності Інтеграл * 0 Інтеграл * Інтеграл *прямокутний трикутник, площа якого дорівнює 2 Інтеграл від алгебраїчної суми двох функцій * Інтеграл Діріхле * р > 1 Інтеграл Діріхле * р Інтеграл з рівними межами інтегрування дорівнює * нулю Інтервалом збіжності степеневого ряду називається такий інтервал: *у всіх внутрішніх точках якого ряд збігається абсолютно Кажуть, що графік функції * всі точки графіка функції лежать вище будь-якої своєї дотичної; Канонічне рівняння параболи, віссю симетрії якої є вісь * Канонічне рівняння параболи, віссю симетрії якої є вісь х записується * Квадратна матриця називається діагональною, якщо всі її елементи, розміщені поза головною діагоналлю, дорівнюють: * 0 Квадратна матриця називається трикутною, якщо всі її елементи, розміщені під або над головною діагоналлю, дорівнюють: * 0 Кожний вектор * Коли будь-яка елементарна функція неперервна? * В кожній точці своєї області існування Коли функція * * Координати середини відрізка * Координати точки * Косинус кута між двома векторами * Критичними точками для заданої функції y=f(x) називають ті значення аргументу х, які *перетворюють похідну функції на нуль Лінійне диференціальне рівняння * Лінійною називається функція виду: * Маємо дві послідовності хп і уп, при чому * Маємо диференціальне рівняння * шукається розв'язок Маємо діагональну матрицю А. Чому дорівнює транспонована матриця * Маємо первісну функції * Маємо рівняння кола * Маємо ряд Діріхле *ряд розбіжний Маємо х – є змінна величина, а – її границя, * Максимум, або мінімум функції називають * Локальним екстремумом Матрицею взаємною *транспонована матриця, складена з алгебраїчних доповнень до її елементів Матриці А і В називаються рівними, якщо для них виконуються умови: * однаковий розмір Матриця В, яка задовольняє співвідношення *оберненою Механічний зміст похідної є: *миттєва швидкість зміни функції в точці Модуль вектора *
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 474; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |


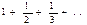
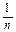






 , де с – стала величина
, де с – стала величина



 , якщо ряди
, якщо ряди  і
і  розбіжні?
розбіжні?
 і
і 

 , якщо
, якщо 



 дорівнює
дорівнює дорівнює:
дорівнює:
 з геометричної точки зору означає
з геометричної точки зору означає дорівнює
дорівнює
 буде збіжним, якщо
буде збіжним, якщо буде розбіжним, якщо
буде розбіжним, якщо
 має в інтервалі
має в інтервалі  опуклість, напрямлену вниз, якщо
опуклість, напрямлену вниз, якщо записується
записується
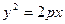

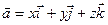


 визначаються формулою
визначаються формулою ,
, 
 , що ділить відрізок у заданому відношенні
, що ділить відрізок у заданому відношенні  , знаходяться за формулами
, знаходяться за формулами ;
; 

 називається однорідним, якщо
називається однорідним, якщо

 і
і  ,
,  . В якому співвідношенні будуть їх границі a і b?
. В якому співвідношенні будуть їх границі a і b?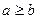
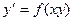 . Задача Коші для даного рівняння полягає в тому, що
. Задача Коші для даного рівняння полягає в тому, що , що задовольняє умові
, що задовольняє умові 
 до матриці А?
до матриці А?
 Яким співвідношенням пов’язані ці функції
Яким співвідношенням пов’язані ці функції
 . Вкажіть координати центра кола і його радіус
. Вкажіть координати центра кола і його радіус ,
, , p=0,1. Як поводиться цей ряд при р=0,1?
, p=0,1. Як поводиться цей ряд при р=0,1? - нескінченно мала величина. Який запис є вірним?
- нескінченно мала величина. Який запис є вірним?
 до матриці А є:
до матриці А є:
 , називається:
, називається: обчислюється за формулою
обчислюється за формулою



