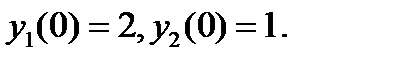Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аппроксимация и интерполяция функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть имеется набор узловых точек xk (где k=1,2,…,n) и значения функции y(xk) в этих точках, а также некоторая функция f(x,a1, a2, …,am), которая кроме аргумента х зависит еще и от параметров as (где s=1, 2, …m). Задача аппроксимации состоит в том, чтобы подобрать такие значения параметров as, что функция f(x, a1, a2, …am) наилучшим образом описывала бы исходную функцию. Как правило, m<<n, поэтому добиться, чтобы функция f(x, a1, a2, …am) давала точные результаты даже в узловых точках не удастся. Нужен критерий, который оценивает точность аппроксимации таблично заданной функции. Например, в методе наименьших квадратов в качестве такого критерия используется среднеквадратическое отклонение
Частным случаем задачи аппроксимации является задача интерполяции функции. В этом случае также имеем набор узловых точек xk (где k=1,2,…,n) и значения функции yk в этих точках. Однако, в соответствии с критерием интерполяции, требуется построить такую функцию f(x), которая в узловых точках x1, x2,…,xn принимала бы значения y1, y2, …,yn, то есть f(xk) = yk для всех k от 1 до n. Чаще всего функцию f(x) ищут в виде полинома, степень которого n-1. Поэтому задача сводится к определению коэффициентов интерполяционного полинома на основании значений функции в базовых точках. На практике для решения задачи интерполяции (вычисления значений функции в точках, несовпадающих с узлами интерполяции) используются интерполяционные формулы Ньютона и формула Лагранжа [1]. Для выполнения полиномиальной аппроксимации в MatLab используется функция polyfit(). Эта функция предназначена для выполнения аппроксимации методом наименьших квадратов. Функция polyfit(x,y,n) возвращает вектор коэффициентов полинома степени n, который с наименьшей среднеквадратичной погрешностью аппроксимирует функцию, заданную таблично. Результатом является вектор строка длиной n+1, содержащий коэффициенты полинома в порядке уменьшения степеней. Аргументами функции являются список узловых точек, список значений интерполируемой функции в этих точках и степень интерполяционного полинома. Как правило, степень полинома много меньше количества узлов (m<<n). В качестве результата возвращается список коэффициентов аппроксимирующего полинома. Ниже приведены пример линейной и кубической аппроксимации функции, заданной таблицей (рис. 2.2.1-1), и графики аппроксимирующих функций (рис. 2.2.1-2).
Рис. 2.2.1-1. Пример линейной и кубической аппроксимации функции
Рис. 2.2.1-2. Графики исходной и аппроксимирующих функций
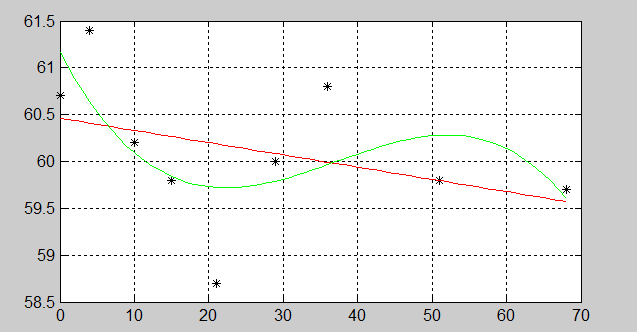
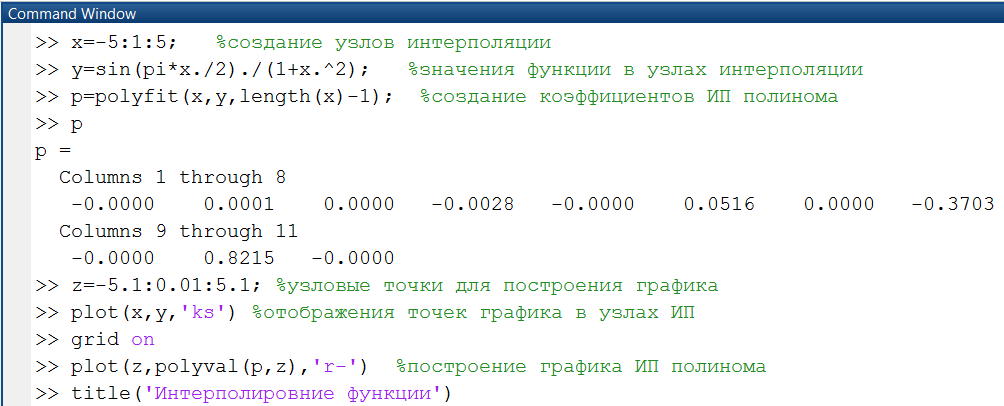
Чтобы результатом выполнения функции Matlab polyfit() был именно интерполяционный полином, необходимо, чтобы степень этого полинома была на единицу меньше количества узловых точек. Пример 2.2.1-1. Используя в качестве узлов интерполяции Выполняя команды Matlab в окне Command Window, получим таблицу значений функции и проведем ее интерполяцию с использованием функции Matlab polyfit() (рис. 2.2.1-3). Графики интерполяционных узлов и интерполяционного полинома приведены на рис. 2.2.1-4.Здесь для вычисления значений полинома в точках используется функция polival(p,z), где вектор z покрывает интервал интерполяции и даже выходит за его пределы.
Рис. 2.2.1-3. Интерполяция таблично заданной функции с использованием функции Matlab polyfit()
Рис. 2.2.1-4. Графики интерполируемой и интерполирующей функций
При большом количестве базовых точек интерполяция полиномом может оказаться малопродуктивной, поэтому нередко используют интерполяцию сплайнами. Идея сплайн-интерполяции состоит в разбиении диапазона интерполирования на отрезки, в пределах которых используются разные функции одного вида (чаще всего алгебраические многочлены). Эта функция и ее несколько производных на всем диапазоне интерполяции непрерывны. В результате имеем кусочно-гладкую интерполяционную зависимость. Сплайн-интерполяцию можно реализовать с помощью функции Matlab interp1(). В качестве аргументов функции передают: набор узловых точек аргумента, значения функции в этих точках, список значений точек, для которых вычисляется значения интерполяционной зависимости и, наконец (в апострофах), тип базового полинома (табл. 2.2.1-1).
Таблица 2.2.1-1
Рассмотрим пример использования функции Matlab interp1().
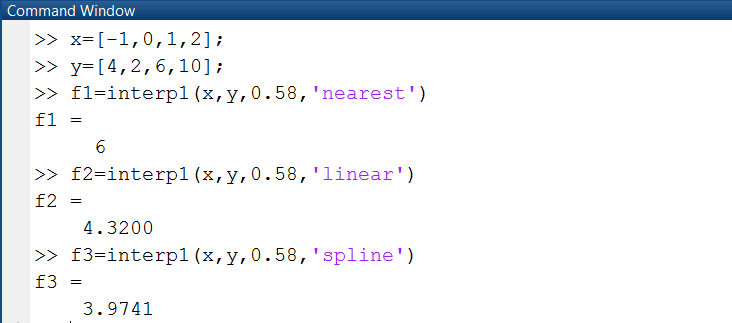
Пример 2.2.1-2. Используя значения интерполирующей функции, заданной таблично, выполнить сплайн-интерполяцию с использованием полиномов нулевой, первой и третьей степени, и получить значения функции в точке х=0.58.
Рис. 2.2.1-5. Вычисление функции в точке х=0.58 На рис. 2.2.1-6 и 2.2.1-7 приведены команды, необходимые для проведения интерполяции таблично заданной функции и построения графиков интерполируемой функции и интерполирующих ее интерполяционных многочленов различных степеней.
Рис. 2.2.2-6. Команды построения графиков интерполяционных функций
Рис. 2.2.2-7. Графики интерполирующих функций
Лабораторная работа по теме «Технология аппроксимации интерполяции функций»
Вопросы, подлежащие изучению
1) Задание векторов и матриц в пакете Matlab. 2) Технология аппроксимации функции, заданной таблично, с использованием функций polyfit (). 3) Технология линейной, кубической и сплайн-интерполяции таблично заданной функции с использованием функций interp1(). 4) Получение интерполяционных многочленов в явном виде. 5) Построение графиков аппроксимирующих и интерполирующих функций.
2. Общее задание
1) Изучите материал Темы 2.2. (п. 2.2.1). 2) Выберите индивидуальное задание: номера узлов и номер аппроксимируемой функции из табл. 2.2.2-1; узлы аппроксимации и значения функции в узлах из табл. 2.2.2-2. 3) Задайте в виде векторов значения узлов и значения функции в выбранных узлах. 4) Вычислите коэффициенты аппроксимирующих функций для линейной, квадратичной и кубической аппроксимации с использованием функции polyfit() и получите три аппроксимирующие функции в явном виде. 5) Получите с использованием этих функций значение аппроксимирующей функции в произвольной точке, принадлежащей отрезку, но не совпадающей с узлами аппроксимации, и сравните полученные результаты. 6) Постройте графики табличной и трех аппроксимирующих функций в одном шаблоне, снабдив их легендой. 7) Проведите линейную и кубическую интерполяцию функции с использованием функции interp1(), заданной таблично. Получив значения интерполирующей функции в точке, не совпадающей с узлами интерполяции, сравните полученные результаты. 8) Постройте графики табличной и двух интерполирующих функций в одном шаблоне, снабдив их легендой. 9) Представьте результаты работы преподавателю, ответьте на поставленные вопросы. 10) Выполните команду clear all. 11) Оформите отчет по выполненной работе. 3. Варианты заданий
Таблица 2.2.2-1
Таблица 2.2.2-2
Содержание отчета 1) В форме комментариев: · Название лабораторной работы · ФИО студента, номер группы · № варианта · Индивидуальное задание 2) Протокол вычислений (сессии) в окне Command Window, снабженный необходимыми комментариями. 2.2.3. Контрольные вопросы по теме 1) Что такое аппроксимация функции и в каких случаях она используется? 2) В чем отличие аппроксимации от интерполяции? 3) Какой метод аппроксимации реализован в функции polyfit()? 4) Что служит результатом выполнения функции polyfit()? 5) Для чего предназначена функция polyval()? 6) Назначение и формат функции interp1()? 7) Каким параметром определяется тип интерполяции в функции interp1()?
Тема 2.3. Технология интегрирования 2.3.1. Вычисление неопределенных и определенных интегралов 2.3.2. Лабораторная работа по теме «Технология интегрирования в среде MatLab» 2.3.3. Контрольные вопросы по теме
2.3.1. Вычисление неопределенных и
При вычислении определенных интегралов первообразную функцию F(x) не всегда удается выразить аналитически, а кроме того иногда подынтегральная функция f(x) задана в виде таблицы (xi и yi, где i = 1, 2, …, n). Это приводит к необходимости использования численных методов интегрирования. Существует ряд методов численного интегрирования. Во всех этих методах вычисление осуществляется по приближенным формулам, называемым квадратурами. Суть получения формул численного интегрирования состоит в том, что на элементарных отрезках интегрирования подынтегральную функцию заменяют простейшим интерполяционным полиномом, который легко может быть проинтегрирован в аналитическом виде. Так, например, для получения формул прямоугольников, трапеций и Симпсона используют полиномы соответственно нулевой, первой и второй степени. Формулы прямоугольников:
где: h – шаг интегрирования; yi – значение подынтегральной функции от аргумента xi, k=0, 1, …,n; n – число разбиений интервала интегрирования a, b. Формула трапеций:
где: h – шаг интегрирования; y0 – значение подынтегральной функции при х = a; yn – значение подынтегральной функции при х = b;
Формула Симпсона:
Для символьного вычисления неопределенных и определенных интегралов используется функция Matlab int(), которая может иметь один из следующих форматов: · int(S) – возвращает символьное значение неопределенного интеграла от символьного выражения или массива символьных выражений S по переменной, которая автоматически определяется функцией findsym(). Если S – скаляр или матрица, то вычисляется интеграл по переменной 'х'. · int(S, v) – возвращает неопределенный интеграл от S по символьной переменной v. · int(S, a, b) – возвращает определенный интеграл от S с пределами интегрирования от а до b, причем пределы интегрирования могут быть как символьными, так и числовыми. · int(S, v, a, b) – возвращает определенный интеграл от S по переменной v с пределами от а до b.
Ниже приведены примеры использования функции Matlab int()
Рис. 2.3.1-1. Примеры вычисления интегралов
В системе MatLab функции вычисления интегралов используют численные методы трапеции, Симпсона и некоторые другие. Рассмотрим технологию интегрирования с использованием некоторых функций. Для вычисления интеграла по формуле трапеции в MatLab используется функция trapz(x,y). Эта функция возвращает значение интеграла Рассмотрим несколько примеров вычисления значений определенных интегралов методом трапеций при различных способах задания узлов подынтегральной функции (рис. 2.3.1-2).
Рис. 2.3.1-2. Вычисление определенных интегралов с использованием ФункцииMatlab trapz()
Для вычисления интеграла по формуле Симпсона в MatLab применяется функция quad(). При обращении к этой функции шаг интегрирования не задается, а используется параметр – требуемая точность вычисления интеграла. Минимальная форма обращения к функции – q=quad('f',a,b), где f – имя функции, взятое в одинарные кавычки, второй и третий аргументы – пределы интегрирования.
Рис. 2.3.1-3. Вычисление определенных интегралов Допускается задание четвертого входного параметра eps – абсолютной погрешности: q=quad('f', a, b, eps ). По умолчанию eps =10-6. Рассмотрим примеры вычисления определенного интеграла
Лабораторная работа по теме «Технология интегрирования в среде Matlab»
Вопросы, подлежащие изучению
1) Получение символьного выражения неопределенного интеграла средствами пакета Matlab. 2) Вычисление значения определенного интеграла с использованием функций. 3) Вычисление значения определенного интеграла с использованием функций Matlab int(), trapz(), quad(). 4) Формулы численного интегрирования: средних прямоугольников, трапеций и Симпсона.
2. Общее задание
1) Изучите материал Темы 2.3 (п. 2.3.1). 2) Выберите из табл. 2.3.2-1 вариант индивидуального задания. 3) Получить символьное выражение неопределенного интеграла с использованием функций int( S) и int( S, x ), где S – символьное выражение, а х - переменная. 4) Вычислите значение определенного интеграла с использованием функции int() формата int( S,a,b ), где a, b – пределы интегрирования. 5) Вычислите определенный интеграл с использованием функции Matlab, реализующей формулу трапеций, - trapz(x, y), предварительно получив таблицу значений подынтегральной функции с шагом h и задав значения аргумента и функции в виде векторов. 6) Вычислите значение определенного интеграла с использованием функции Matlab, реализующей формулу Симпсона, – quad('f',a,b), где f – имя функции, взятое в одинарные кавычки. 7) Представьте результаты работы преподавателю, ответьте на поставленные вопросы. 8) Выполните команду clear all. 9) Оформите отчет по выполненной работе. Варианты индивидуальных заданий
Таблица 2.3.2-1
Содержание отчета
1) В форме комментариев: · Название лабораторной работы · ФИО студента, номер группы · № варианта · Индивидуальное задание 2) Протокол вычислений (сессии) в окне Command Window, снабженный необходимыми комментариями. 2.3.3. Контрольные вопросы по теме 1) Какой функцией в Matlab определяется символьное значение определенного интеграла? 2) Назначение функции trap(x,y). 3) Что возвращает функция trap(x,y), если y(x) – матрица? 4) Можно ли использовать функцию trap(x,y), если узлы по оси х - не равноотстоящие? 5) Какая функция Matlab позволяет вычислить определенный интеграл с заданной точностью? 6) Способы задания подынтегральной функции при вычислении определенного интеграла с использованием функции quad(). 7) Какова точность вычисления определенного интеграла по умолчанию? Тема 2.4. Технология решения обыкновенных 2.4.1. Численное решение обыкновенных дифференциальных уравнений 2.4.2. Лабораторная работа по теме 2.4.3. Контрольные вопросы по теме 2.4.1. Численное решение обыкновенных Представим обыкновенное дифференциальное уравнение (ОДУ) первого порядка в виде, разрешенном относительно производной Тогда решением ОДУ является функция Задача Коши при решении ОДУ n-го порядка
Результатом решения ОДУ численными методами является таблица значений y = j(x) на некотором множестве значений аргументов. Поэтому при постановке задачи численного решения ОДУ наряду с начальными условиями x0, y0 необходимо задать область решения – отрезок [a;b] и шаг изменения аргумента h (шаг интегрирования). Для получения численного решения ОДУ используются методы Рунге-Кутты [1]. Методы различаются порядком. Чем выше порядок метода, тем точнее решение, полученное при равном шаге интегрирования.
В Matlab имеется несколько функций для решения задачи Коши. Рассмотрим две функции, используемые для решения обыкновенных дифференциальных уравнений (ОДУ): ode23() – использует метод Рунге-Кутты второго и третьего порядка; ode45() – использует метод Рунге-Кутты четвёртого и пятого порядка точности с автоматическим выбором шага. В MatLab обращением к функциям, предназначенным для решения ОДУ, является: [x, y] = ode23('fun',t0,tf,x0) [x, y] = ode45('fun',t0,tf,x0)
Входными параметрами функций являются: · 'fun' – имя функции (в виде строчной переменной) или ссылка на функцию, задающую правую часть дифференциального уравнения (уравнение должно быть записано в нормальной форме · t0 – начальное значение аргумента; · tf – конечное значение аргумента; · х0 – вектор начальных условий.
Выходными параметрами функций являются: · x – вектор, содержащий отсчёты аргумента в точках решения; · y – вектор, содержащий вычисленные значения результата решения ОДУ в точках, соответствующих отсчетам независимой перемен-ной x.
Требования к точности и другие параметры численного решения задаются в Matlab по умолчанию. Изменить эти настройки позволяет дополнительный аргумент OPTIONS.
Рис. 2.4.1-1. Решение ОДУ методом Рунге-Кутты второго порядка
Рассмотрим примеры использования функций ode23() и ode45() для решения ОДУ вида: На рис. 2.4.1-2 приведено решение того же ОДУ, но с использованием функции ode45(). Вывод таблицы решения дополнен графиком функции y(x) (рис. 2.4.1-3).
Рис. 2.4.1-2. Решение ОДУ методом Рунге-Кутты четвертого порядка
Рис. 2.4.1-3. Графическое решение ОДУ
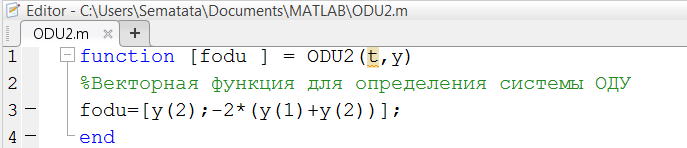
При решении ОДУ высокого порядка вводят обозначения (новые функции) для всех производных, кроме самой старшей. В этих обозначениях самая старшая производная становится записанной, как первая. Исходное уравнение дополняется тождествами, определяющими правила введения новых функций. Проиллюстрируем описанный подход при решении ОДУ второго порядка. Требуется решить Решение системы ОДУ в Matlab начинается с определения векторной функции (рис. 2.4.1-4).
Рис. 2.4.1-4. Определение векторной функции
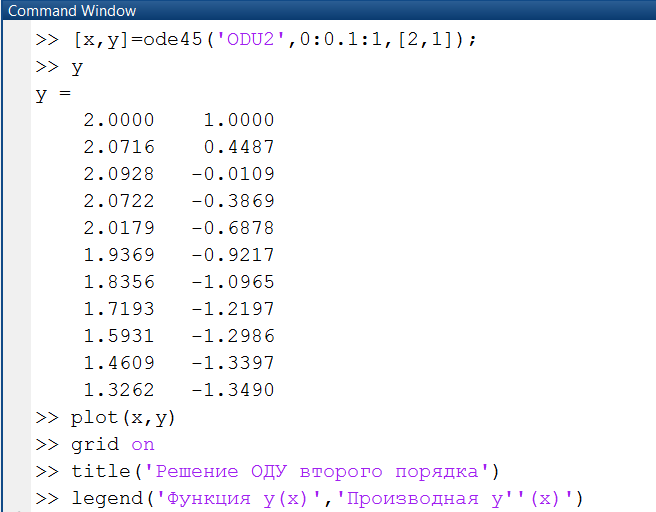
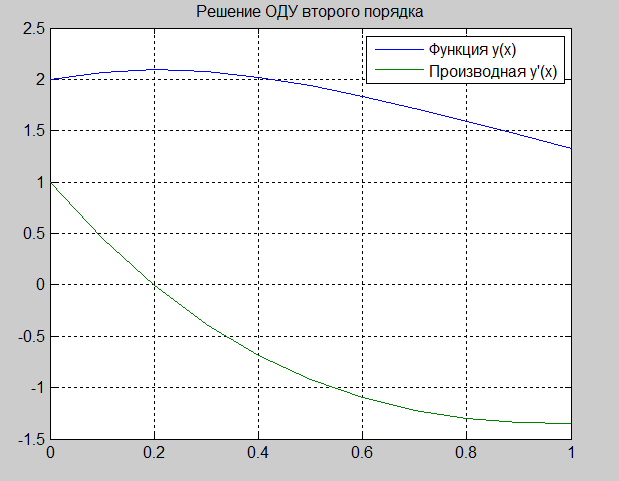
Для решения дифференциального уравнения (системы уравнений) используем команды, где решение системы ОДУ записывается в переменную y. При этом элемент y(1) содержит значение функции y(x), а y(2) значение производной y'(x). Команда plot(x, y) строит график функции решения ОДУ и ее производной (рис. 2.4.1-6).
Рис. 2.4.1-5. Решение ОДУ второго порядка
Рис. 2.4.1-6. Графики функций решения ОДУ и производной Лабораторная работа по теме «Технология решения обыкновенных
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 4967; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.54.199 (0.011 с.) |

 .
.
 .
.








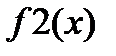


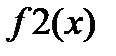
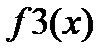

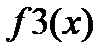
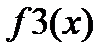
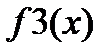
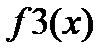
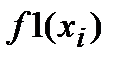
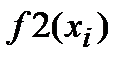
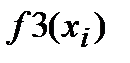

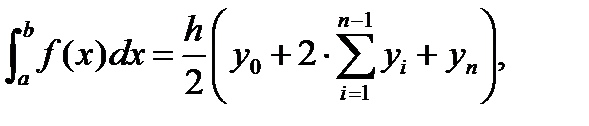
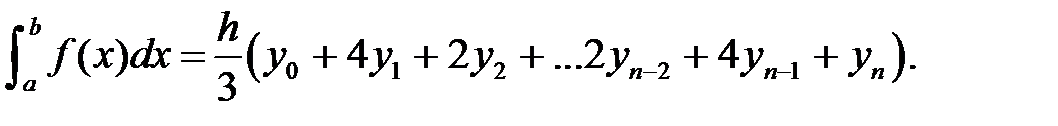

 от функции y(x), которая может быть представлена вектором или матрицей. Если y(x) – матрица, то функция возвращает вектор значений интеграла каждого столбца матрицы. Если вектор узлов не задан - trapz(y), то в качестве ординат x используются индексы вектора y (x=1:length(y)), где функция определяет длину вектора y. Важно, что узлы по оси x могут быть как равноотстоящими, так и неравноотстоящими.
от функции y(x), которая может быть представлена вектором или матрицей. Если y(x) – матрица, то функция возвращает вектор значений интеграла каждого столбца матрицы. Если вектор узлов не задан - trapz(y), то в качестве ординат x используются индексы вектора y (x=1:length(y)), где функция определяет длину вектора y. Важно, что узлы по оси x могут быть как равноотстоящими, так и неравноотстоящими.

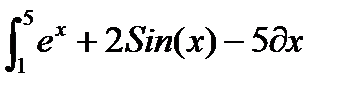 с использованием функции Matlab quad() (рис. 2.3.1-3).
с использованием функции Matlab quad() (рис. 2.3.1-3).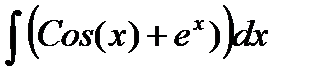
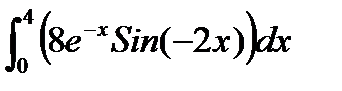

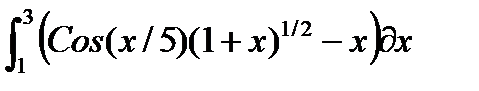

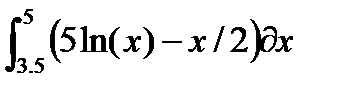

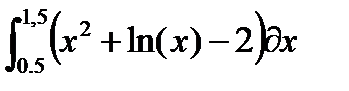
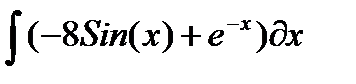
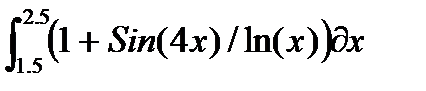
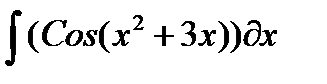
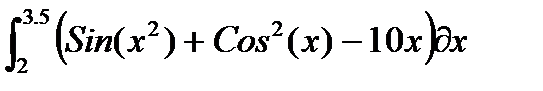
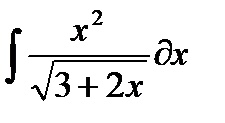
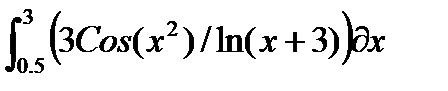
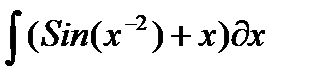
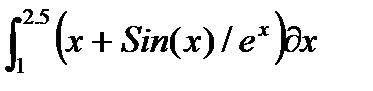
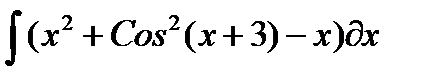



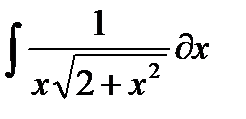
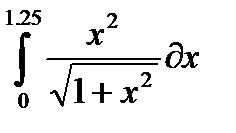
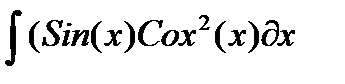

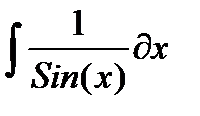
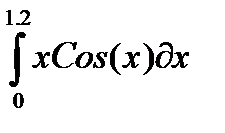
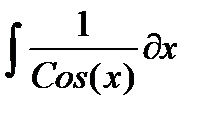
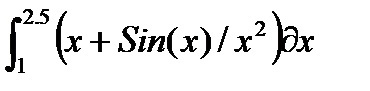
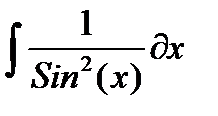
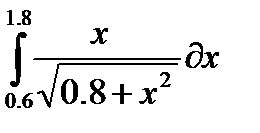

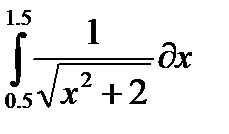
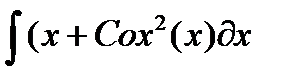

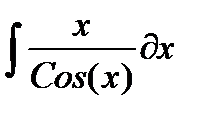
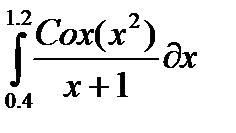
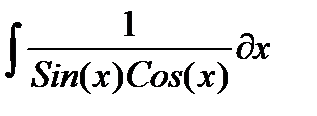
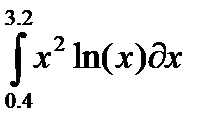
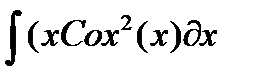


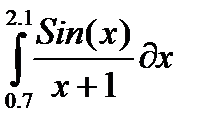
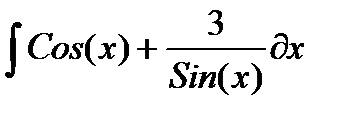
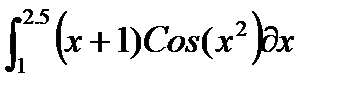
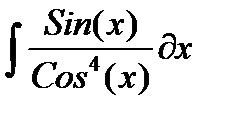
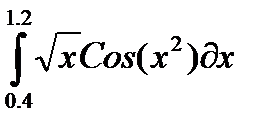
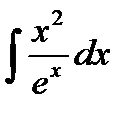


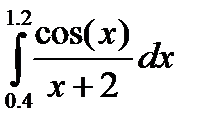
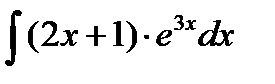
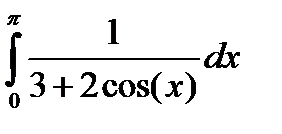
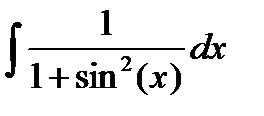
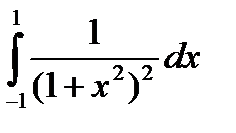
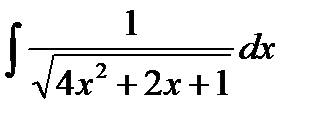
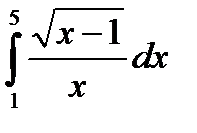
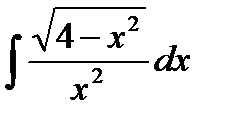
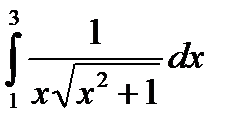

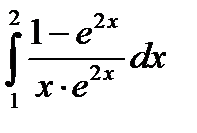
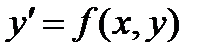 , и пусть
, и пусть  – начальные условия его решения.
– начальные условия его решения.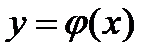 , которая, будучи подставленной в исходное уравнение, обратит его в тождество, и одновременно будут выполняться начальные условия. Эта задача в математике называется задачей Коши.
, которая, будучи подставленной в исходное уравнение, обратит его в тождество, и одновременно будут выполняться начальные условия. Эта задача в математике называется задачей Коши.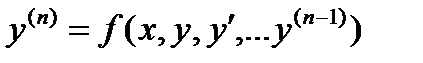 формулируется аналогично, при этом начальными условиями должны быть:
формулируется аналогично, при этом начальными условиями должны быть: 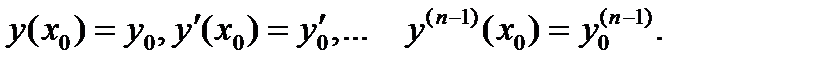 При решении ОДУ n-го порядка уравнение путем выполнения ряда обозначений
При решении ОДУ n-го порядка уравнение путем выполнения ряда обозначений  представляется в виде системы дифференциальных уравнений:
представляется в виде системы дифференциальных уравнений:

 на отрезке [1;10] с шагом интегрирования 1 при начальных условиях y(1)=1. Решение ОДУ с использованием функции ode23() приведено на рис. 2.4.1-1.
на отрезке [1;10] с шагом интегрирования 1 при начальных условиях y(1)=1. Решение ОДУ с использованием функции ode23() приведено на рис. 2.4.1-1.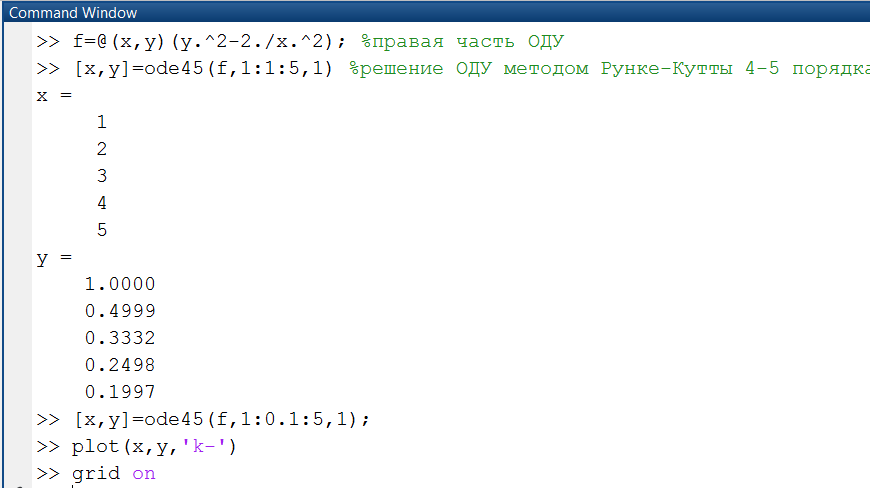
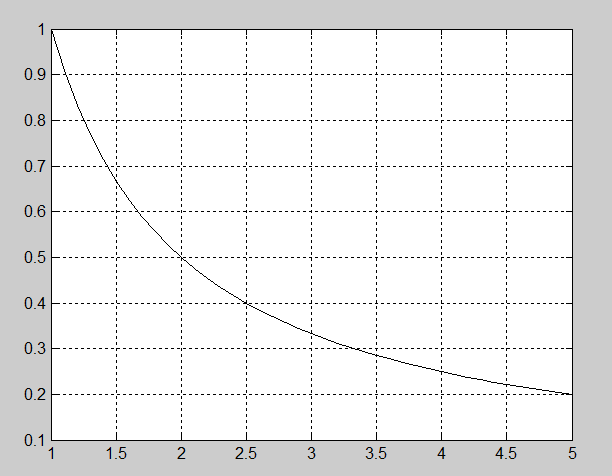
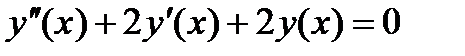 с начальными условиями: и
с начальными условиями: и 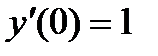 . Сведем заданное ОДУ к равноценной системе ОДУ первого порядка. Для этого переобозначим функцию
. Сведем заданное ОДУ к равноценной системе ОДУ первого порядка. Для этого переобозначим функцию 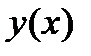 , как
, как  , и введем функцию
, и введем функцию  . Запишем исходное уравнение в новых обозначениях:
. Запишем исходное уравнение в новых обозначениях: 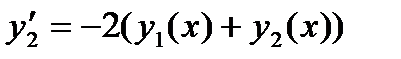 (здесь учтено, что
(здесь учтено, что  ). Дополним это уравнение тождеством
). Дополним это уравнение тождеством 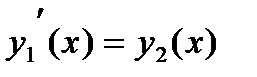 и получим нужную систему ОДУ. Эту систему следует дополнить начальными условиями:
и получим нужную систему ОДУ. Эту систему следует дополнить начальными условиями: