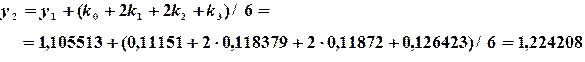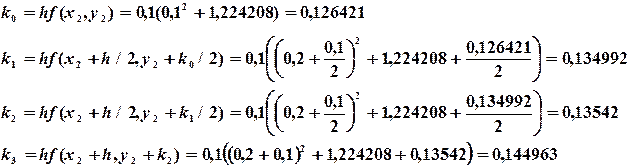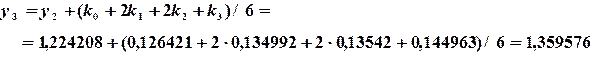Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближение функции по методу наименьших квадратов (МНК).Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторным и самостоятельным работам по курсам «Информатика» и «Вычислительная математика»
ЧИСЛЕННЫЕ МЕТОДЫ
ЧАСТЬ 2
Казань УДК 621.313: 518.6
Составители: Ф.Г.Ахмадиев, Ф.Г.Габбасов, Р.Ф.Гиззятов, И.В.Маланичев.
Методические указания к лабораторным и самостоятельным работам по курсам "Информатика" и «Вычислительная математика». Численные методы. Часть 2. /Казанский государственный архитектурно-строительный университет. Сост.: Ф.Г.Ахмадиев, Ф.Г.Габбасов, Р.Ф.Гиззятов, И.В.Маланичев. – Казань, 2011. – 36 с.
Методические указания состоят из двух частей и предназначены для выполнения лабораторных и самостоятельных работ студентами всех специальностей и направлений подготовки дневного и заочного отделений. В данной части приводятся численные методы аппроксимации функций, вычисления определенных интегралов, решения дифференциальных уравнений и задач линейного программирования.
Рецензент – Р.Б.Салимов, доктор физ.-мат. наук, профессор
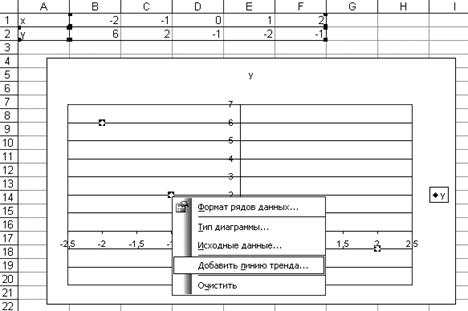
Казанский государственный ã архитектурно-строительный университет, 2011 г. Аппроксимация функций. Порядок решения. 1) Ввести таблицу в рабочий лист Excel (рис. 4.1). Выделить ячейки таблицы. 2) Вызвать Мастер диаграмм. Выбрать тип диаграммы – точечная (без соединительных линий). Нажать кнопку «Готово». На рабочем листе появится график точек таблицы.
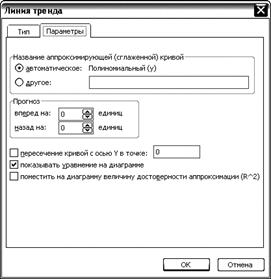
3) Вызвать контекстное меню (правой кнопкой мыши) одной из точек графика. Выбрать пункт «добавить линию тренда». 4) На вкладке тип выбрать полиномиальная аппроксимация и установить степень полинома равной 2 (рис. 4.2). 5) На вкладке параметры отметить «показывать уравнение на диаграмме».
6) Закрыть окно настроек, нажав кнопку ОК. Появляется линия графика аппроксимирующей функции и соответствующая формула (рис. 4.3):
Аппроксимация линеаризацией. Многие нелинейные функции, зависящие от двух параметров, можно линеаризовать путем замены переменных. Для этого необходимо подобрать такое преобразование исходной зависимости
Пример 4.4. Используя МНК, построить эмпирическую зависимость
Решение. Расчеты представим в виде таблицы.
Система для определения коэффициентов имеет вид:
Решая систему (4.10), получим следующие значения параметров: Тогда (табл. 4.6) Эмпирическая зависимость имеет вид:
Аппроксимация произвольной функцией может быть выполнена в программе Excel с помощью модуля «Поиск решения». Пример 4.5. Используя программу Excel, построить эмпирическую зависимость, аппроксимирующую значения из таблицы:
Порядок решения. 1) Аппроксимирующая функция должна иметь экстремум в виде пика. Выберем следующую функцию, зависящую от трех параметров 2) Ввести в ячейки A2, B2, C2 (рис. 4.4) начальные значения параметров 3) В ячейки A5:A11 – значения 4) В ячейки B5:B11 – значения 5) В ячейку C5 – формулу аппроксимирующей функции (на ячейки с параметрами абсолютные ссылки): =$A$2*EXP(-((A5-$B$2)^2)/$C$2) 6) Скопировать формулу в ячейки C6:C11 7) В ячейку D5 – формулу квадрата разности: =(B5-C5)^2 8) Скопировать формулу в ячейки D6:D11 9) В ячейку D12 – сумму квадратов: =СУММ(D5:D11) 10) Вызвать окно Поиск решения. В настройках указать: Установить целевую ячейку $D$12 Равной минимальному значению Изменяя ячейки $A$2:$C$2 11) Нажать кнопку Выполнить. 12) Подтвердить сохранение найденного решения. 13) Рабочий лист изменился и содержит решение (рис. 4.4):
Таким образом, аппроксимирующая данные табл. 4.9 функция имеет вид:
Точность аппроксимации можно оценить среднеквадратической ошибкой
которая не должна превышать погрешность исходных данных. 4.2. Интерполяционный полином в форме Лагранжа. При решении дифференциальных, интегральных уравнений численными методами вместо искомой функции, обычно, определяют ее значения в отдельных точках (узлах). На следующем этапе проводят восстановление аналитической функции по заданным узлам. Интерполяция интересует нас главным образом как один из способов построения многочлена, приближающего функцию на данном отрезке. Пусть на некотором промежутке
Этот полином называется интерполяционным полиномом, является единственным полиномом степени Интерполяционный полином Лагранжа имеет следующую формулу:
где
и зависят лишь от заданных узлов
Пример 4.5. Пусть задана таблица:
Необходимо построить интерполяционный полином Лагранжа, проходящий через заданные точки Решение. Запишем фундаментальные полиномы Лагранжа:
Проверим свойство (4.11), например, для
Подставляя
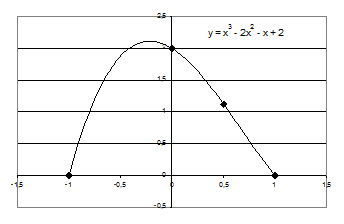
Порядок решения. 14) Ввести таблицу в рабочий лист Excel (обыкновенные дроби вводятся как формулы, т.е. =9/8). Выделить ячейки таблицы. 15) Вызвать Мастер диаграмм. Выбрать тип диаграммы – точечная (без соединительных линий). Нажать кнопку «Готово». 16) Вызвать контекстное меню (правой кнопкой мыши) одной из точек графика. Выбрать пункт «добавить линию тренда». 17) На вкладке тип выбрать полиномиальная аппроксимация и установить степень полинома на единицу меньше числа точек, т.е. 3. 18) На вкладке параметры отметить «показывать уравнение на диаграмме». 19) Закрыть окно настроек, нажав кнопку ОК. Появляется линия графика интерполирующей функции и соответствующая формула:
Численное интегрирование. Требуется вычислить определенный интеграл:
Выберем на отрезке интегрирования
и интерполируем функцию
которая называется квадратурной формулой интерполяционного типа. Метод прямоугольников. На каждом отрезке Поэтому приближенно I вычисляется по формуле (см. рис. 5.1):
Для равноотстоящих узлов формула (5.3) имеет следующий вид:
Или
Формулу (5.4) называют формулой левых прямоугольников, а (5.5) - правых прямоугольников. Программа вычисления интеграла методом прямоугольников представлена на рис. 5.2.
Метод трапеций. В этом методе на каждом отрезке По формуле Лагранжа:
Интегрируя
Суммируя по всем
Для равноотстоящих узлов
или
Программа вычисления интеграла методом трапеций: в программе, представленной на рис. 5.2, заменить отмеченные строки на следующие: 1 S=S+0.5*(FNF(x)+FNF(X+H))*H X=X+H 5.3. Метод парабол (Симпсона). Интервал По формуле Лагранжа:
Интегрируя
Суммируяформулу (5.14)по всем
или
Программа вычисления интеграла методом парабол (Симпсона): в программе, представленной на рис. 5.2, заменить отмеченные строки на следующие: 1 S=S+(FNF(X)+4*FNF(X+H)+FNF(X+2*H))*H/3 X=X+2*H Порядок решения. 20) Ввести в ячейки A1:F1 заголовки столбцов (рис. 5.5). 21) В ячейку A2 – нижний предел интеграла 22) В ячейку E2 – шаг разбиения 23) В ячейку A3 – значение 24) Выделить ячейки A2:A3 и при помощи маркера заполнения ввести значения 25) В ячейку B2 – формулу 26) Выделить ячейку B2 и при помощи маркера заполнения ввести значения 27) В ячейки С2, C3, … – коэффициенты 28) В ячейку D2 – формулу 29) Выделить ячейку D2 и при помощи маркера заполнения ввести значения 30) В ячейке D11 найти сумму чисел столбца D, используя кнопку Автосумма 31) В ячейке F11 найти значение интеграла =D11*E2
Метод Эйлера. Одним из простейших разностных методов решения обыкновенного дифференциального уравнения является одношаговый метод Эйлера. Пусть требуется решить задачу Коши для уравнения первого порядка:
на отрезке На данном отрезке выбираем некоторую совокупность узловых точек
Соотношения (6.6) имеют вид рекурентных формул, с помощью которых значение сеточной функции
Программа решения задачи Коши методом Эйлера дана на рис. 6.2.
Пример 6.1. Решить задачу Коши методом Эйлера для дифференциального уравнения
Решение. По формуле (6.6) вычислим значение
Аналогично вычисляются последующие значения функции в узловых точках
Сеточную функцию записываем в виде таблицы
Порядок решения. 1) Ввести в ячейки A1:D1 заголовки столбцов (рис. 6.4). 2) В ячейку A2 – 3) В ячейки B2 и C2 – 4) В ячейку D2 – шаг интегрирования 5) В ячейку A3 – значение 6) В ячейку B3 – формулу 7) В ячейку С3 – формулу 8) Выделить ячейки A3:С3 и при помощи маркера заполнения ввести формулы в ячейки A4:С4 … A13:С12. 9) Столбцы A и С содержат решение.
Метод Рунге-Кутта. На основе метода Рунге-Кутта могут быть построены разностные схемы разного порядка точности. Наиболее употребительной является следующая схема четвертого порядка:
где
Таким образом, метод Рунге-Кутта требует на каждом шаге четырехкратного вычисления правой части уравнения. Однако это окупается повышенной точностью, что дает возможность проводить счет с относительно большим шагом. Программа решения задачи Коши методом Рунге-Кутта отличается от приведенной на рис. 6.2 заменой отмеченных строк на следующие: 1 K0 = H*FNY(X,Y) K1 = H*FNY(X+H/2,Y+K0/2) K2 = H*FNY(X+H/2,Y+K1/2) K3 = H*FNY(X+H,Y+K2) Y=Y+(K0+2*K1+2*K2+K3)/6 Пример 6.4. Решить задачу Коши методомРунге-Кутта для дифференциального уравнения Решение. По формулам (6.12) вычислим значения
Используя формулу (6.11), находим значение
Аналогично вычисляются последующие значения функции в узловых точках
Сеточную функцию записываем в виде таблицы
Порядок решения. 1) Ввести данные задачи в рабочий лист (рис. 7.3); 2) Ввести в ячейки B2, C2 начальный план, например 0 0 3) В ячейку D4 – формулу расчета затрат первого вида ресурсов (на ячейки плана абсолютные ссылки): =B4*$B$2+C4*$C$2 4) Скопировать формулу в ячейки D5:D6 5) В ячейку E8 – формулу расчета дохода: =B8*$B$2+C8*$C$2
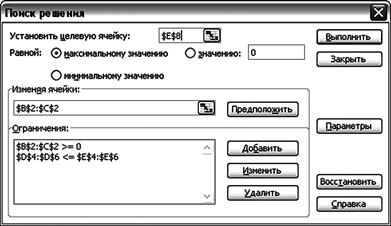
6) Вызвать окно Поиск решения. В настройках указать (рис. 7.4): Установить целевую ячейку $E$8 Равной максимальному значению Изменяя ячейки $B$2:$C$2
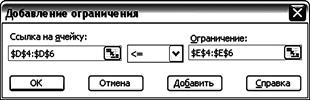
7) Нажать кнопку Добавить. Добавить ограничения на ресурсы (рис. 7.5) $D$4:$D$6<=$E4$E6 8) Нажать кнопку Добавить. Добавить условие неотрицательности переменных плана $B$2:$C$2>=0 9) Нажать кнопку OK.
10) Нажать кнопку Выполнить. 11) Подтвердить сохранение найденного решения. 12) Рабочий лист изменился и содержит решение (рис. 7.6):
Следует выпускать 35 единиц продукции вида А и 30 единиц продукции вида Б. Максимально возможный доход составит 710 $. ЛИТЕРАТУРА 1. Калиткин Н.П. Численные методы. М.: Наука, 1978. - 512 с. 2. Турчак Л.И., Плотников П.В. Основы численных методов: Учебное пособие. М.: ФИЗМАТЛИТ, 2003. – 304 с. 3. Васильев А.Н. Научные вычисления в Microsoft Excel. М.: Издательский дом "Вильямс", 2004. – 512 с. 4. Ларсен У.Р. Инженерные расчеты в Excel. М.: Издательский дом "Вильямс", 2004. – 544 с. 5. Попов В.И. Численные методы расчета мостовых конструкций на ЭВМ. М.: 1981. – 78 с. 6. Ф.Г.Ахмадиев, Ф.Г.Габбасов, И.Н.Гатауллин, Р.Ф.Гиззятов, Р.И.Ибятов, Х.Г.Киямов. Методические указания к лабораторным работам по курсу «Информатика» для всех специальностей. Численные методы. Часть 1. КГАСУ, 2008г., 34с. 7. Ф.Г.Ахмадиев, Ф.Г.Габбасов, И.Н.Гатауллин, Р.Ф.Гиззятов, Р.И.Ибятов, Х.Г.Киямов. Методические указания к лабораторным работам по курсу «Информатика» для всех специальностей. Численные методы. Часть 2. КГАСУ, 2008г., 35с.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторным и самостоятельным работам по курсам «Информатика» и «Вычислительная математика»
ЧИСЛЕННЫЕ МЕТОДЫ
ЧАСТЬ 2
Казань УДК 621.313: 518.6
Составители: Ф.Г.Ахмадиев, Ф.Г.Габбасов, Р.Ф.Гиззятов, И.В.Маланичев.
Методические указания к лабораторным и самостоятельным работам по курсам "Информатика" и «Вычислительная математика». Численные методы. Часть 2. /Казанский государственный архитектурно-строительный университет. Сост.: Ф.Г.Ахмадиев, Ф.Г.Габбасов, Р.Ф.Гиззятов, И.В.Маланичев. – Казань, 2011. – 36 с.
Методические указания состоят из двух частей и предназначены для выполнения лабораторных и самостоятельных работ студентами всех специальностей и направлений подготовки дневного и заочного отделений. В данной части приводятся численные методы аппроксимации функций, вычисления определенных интегралов, решения дифференциальных уравнений и задач линейного программирования.
Рецензент – Р.Б.Салимов, доктор физ.-мат. наук, профессор
Казанский государственный ã архитектурно-строительный университет, 2011 г. Аппроксимация функций. Приближение функции по методу наименьших квадратов (МНК). Очень часто в практической работе возникает необходимость найти в явном виде функциональную зависимость между величинами |


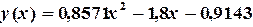

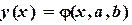 , в результате которого она приобретает линейный вид
, в результате которого она приобретает линейный вид 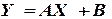 . Далее решается задача линейной аппроксимации для новой зависимости и вычисленые коэффициенты
. Далее решается задача линейной аппроксимации для новой зависимости и вычисленые коэффициенты  и
и  пересчитываются в
пересчитываются в  и
и 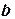 .
.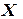
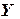
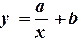
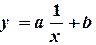
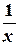
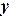
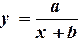
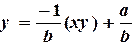
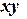

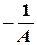
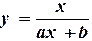

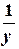
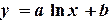


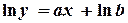
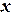


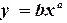

 , аппроксимирующую следующие табличные значения:
, аппроксимирующую следующие табличные значения: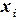
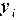
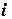

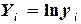
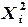


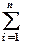
 (4.10)
(4.10)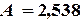 ,
, 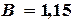 .
.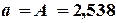 ,
,  .
.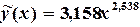
 :
:  ;
;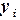
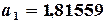
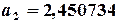



 ,
, заданы
заданы  различных узлов
различных узлов 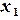 ,
,  ,
, 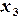 , …,
, …,  , а также значения некоторой функции
, а также значения некоторой функции 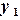 ,
,  ,
, 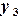 , …,
, …, 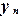 в этих узлах. Необходимо построить полином
в этих узлах. Необходимо построить полином 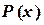 , проходящий через заданные точки, т.е.
, проходящий через заданные точки, т.е.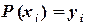
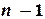 , и может быть записан, например, в форме Лагранжа или Ньютона.
, и может быть записан, например, в форме Лагранжа или Ньютона. (4.11)
(4.11)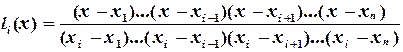 -фундаментальные полиномы Лагранжа. Они удовлетворяют равенствам
-фундаментальные полиномы Лагранжа. Они удовлетворяют равенствам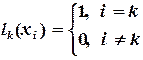 (4.12)
(4.12)
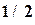
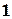


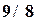
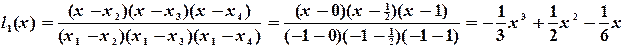

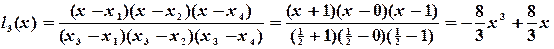
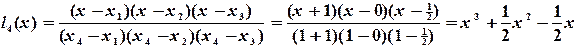
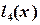 :
: ,
,  ,
, 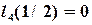 ,
, 
 в полином Лагранжа находим:
в полином Лагранжа находим: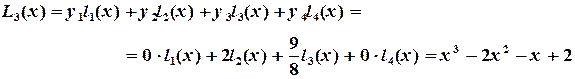

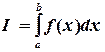 (5.1)
(5.1)
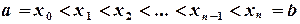
 по ее значениям в этих узлах некоторым полиномом
по ее значениям в этих узлах некоторым полиномом  . Тогда определенный интеграл (5.1) приближенно можно вычислять по формуле
. Тогда определенный интеграл (5.1) приближенно можно вычислять по формуле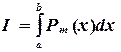 , (5.2)
, (5.2)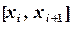 ,
, 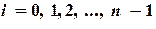 функция
функция 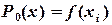 .
.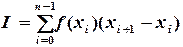 (5.3)
(5.3)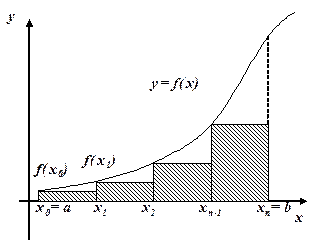
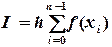 ,
,  (5.4)
(5.4)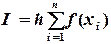 (5.5)
(5.5)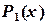 .
. (5.9)
(5.9) (5.10)
(5.10)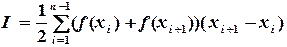 (5.11)
(5.11)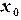 ,
, 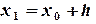 , …,
, …, 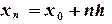 формула (5.11) принимает следующий вид:
формула (5.11) принимает следующий вид: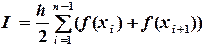 (5.12)
(5.12) (5.13)
(5.13)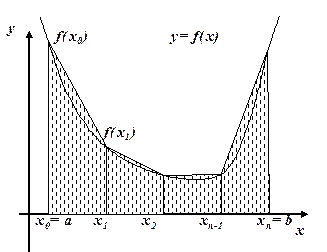
 отрезков. Группируя узлы тройками
отрезков. Группируя узлы тройками 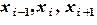 , на каждом отрезке
, на каждом отрезке 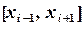
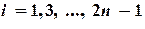 интерполируемфункцию
интерполируемфункцию 

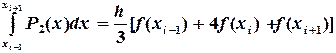 (5.14)
(5.14) (5.15)
(5.15) (5.15)
(5.15)
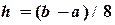 для
для 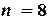 =(1-0)/8
=(1-0)/8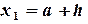 0,125
0,125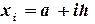 до
до 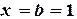 в столбце A.
в столбце A. в столбце B.
в столбце B.
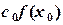 =B2*C2
=B2*C2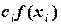 в столбце D.
в столбце D. .
.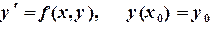 (6.5)
(6.5) .
. и разложим искомую функцию
и разложим искомую функцию  в ряд Тейлора в их окрестностях. Если отбросить все члены, содержащие производные второго и более высоких порядков, и считать узлы равностоящими, т.е.
в ряд Тейлора в их окрестностях. Если отбросить все члены, содержащие производные второго и более высоких порядков, и считать узлы равностоящими, т.е.  , то это разложение можно записать в виде:
, то это разложение можно записать в виде: ,
, 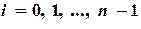 (6.6)
(6.6) в любом узле
в любом узле 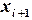 вычисляется по ее значению
вычисляется по ее значению  . На каждом шаге погрешность имеет порядок
. На каждом шаге погрешность имеет порядок  . На рис. 6.1 дана геометрическая интерпретация метода Эйлера. В силу невысокой точности формулой Эйлера редко пользуются в практических расчетах и используют более точные методы. Например, модифицированный метод Эйлера.
. На рис. 6.1 дана геометрическая интерпретация метода Эйлера. В силу невысокой точности формулой Эйлера редко пользуются в практических расчетах и используют более точные методы. Например, модифицированный метод Эйлера.
 на отрезке
на отрезке  с шагом
с шагом 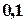
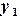



 1
1 0,1
0,1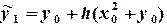 =C2+$D$2*(A2^2+C2)
=C2+$D$2*(A2^2+C2) =C2+$D$2*(A2^2+C2+A3^2+B3)/2
=C2+$D$2*(A2^2+C2+A3^2+B3)/2 (6.11)
(6.11) (6.12)
(6.12) ,
,  ,
,  ,
,  :
:
 :
: