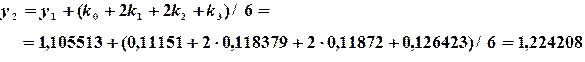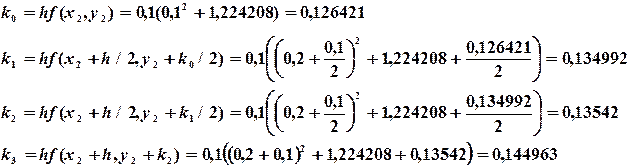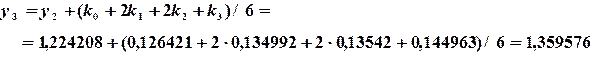Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модифицированный метод Эйлера.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Модифицированный метод Эйлера позволяет уменьшить погрешность на каждом шаге до величины
Аппроксимируем вторую производную с помощью отношения конечных разностей:
Подставляя это соотношение в (6.7) и пренебрегая членами порядка
Полученная схема является неявной, поскольку искомое значение
Найденное значение подставляется вместо
На рис. 6.3 дана геометрическая интерпретация первого шага вычислений при решении задачи Коши модифицированным методом Эйлера.
Пример 6.2. Решить задачу Коши модифицированным методом Эйлера для дифференциального уравнения
Решение. По формуле (6.9) вычислим первое приближение
Используя формулу (6.10), находим окончательное значение в точке
Аналогично вычисляются последующие значения функции в узловых точках
Сеточную функцию записываем в виде таблицы
Программа решения задачи Коши модифицированным методом Эйлера отличается от приведенной на рис. 6.2 заменой отмеченных строк на следующие:
1 Y1=Y+ FNY(X,Y)*H Y=Y+H*(FNY(X,Y)+FNY(X+H,Y1))/2 Пример 6.3. Решить задачу Коши модифицированным методом Эйлера с помощью программы Excel для дифференциального уравнения
Порядок решения. 1) Ввести в ячейки A1:D1 заголовки столбцов (рис. 6.4). 2) В ячейку A2 – 3) В ячейки B2 и C2 – 4) В ячейку D2 – шаг интегрирования 5) В ячейку A3 – значение 6) В ячейку B3 – формулу 7) В ячейку С3 – формулу 8) Выделить ячейки A3:С3 и при помощи маркера заполнения ввести формулы в ячейки A4:С4 … A13:С12. 9) Столбцы A и С содержат решение.
Метод Рунге-Кутта.
На основе метода Рунге-Кутта могут быть построены разностные схемы разного порядка точности. Наиболее употребительной является следующая схема четвертого порядка:
где
Таким образом, метод Рунге-Кутта требует на каждом шаге четырехкратного вычисления правой части уравнения. Однако это окупается повышенной точностью, что дает возможность проводить счет с относительно большим шагом. Программа решения задачи Коши методом Рунге-Кутта отличается от приведенной на рис. 6.2 заменой отмеченных строк на следующие: 1 K0 = H*FNY(X,Y) K1 = H*FNY(X+H/2,Y+K0/2) K2 = H*FNY(X+H/2,Y+K1/2) K3 = H*FNY(X+H,Y+K2) Y=Y+(K0+2*K1+2*K2+K3)/6 Пример 6.4. Решить задачу Коши методомРунге-Кутта для дифференциального уравнения Решение. По формулам (6.12) вычислим значения
Используя формулу (6.11), находим значение
Аналогично вычисляются последующие значения функции в узловых точках
Сеточную функцию записываем в виде таблицы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 2796; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.210.41 (0.009 с.) |

 вместо
вместо  в обычном методе (6.6). Запишем разложение функции в ряд Тейлора в виде:
в обычном методе (6.6). Запишем разложение функции в ряд Тейлора в виде: (6.7)
(6.7)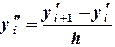
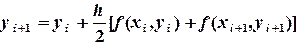 (6.8)
(6.8) входит в обе части соотношения (6.8) и его нельзя выразить явно. Если имеется хорошее начальное приближение
входит в обе части соотношения (6.8) и его нельзя выразить явно. Если имеется хорошее начальное приближение 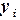 , то можно построить решение с использованием двух итераций следующим образом. Сначала по формуле (6.6) вычисляют первое приближение
, то можно построить решение с использованием двух итераций следующим образом. Сначала по формуле (6.6) вычисляют первое приближение 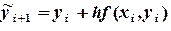 (6.9)
(6.9)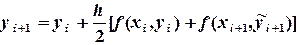 (6.10)
(6.10)
 на отрезке
на отрезке  с шагом
с шагом 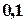







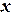
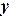
 с шагом
с шагом 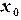 0
0 1
1 0,1
0,1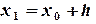 =A2+$D$2
=A2+$D$2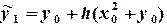 =C2+$D$2*(A2^2+C2)
=C2+$D$2*(A2^2+C2) =C2+$D$2*(A2^2+C2+A3^2+B3)/2
=C2+$D$2*(A2^2+C2+A3^2+B3)/2 (6.11)
(6.11) (6.12)
(6.12) ,
,  ,
,  ,
,  :
:
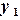 в точке
в точке