
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модифицированный метод ЭйлераСодержание книги
Поиск на нашем сайте
Точность метода Эйлера можно существенно повысить, улучшив аппроксимацию производной. Это можно сделать, например, используя среднее значение производной в начале и в конце интервала. В модифицированном методе Эйлера сначала по методу Эйлера вычисляется значение функции в следующей точке: y*i+1 = yi + h×f(xi,yi), которое используется для вычисления приближённого значения производной в конце интервала f(xi+1, y*i+1). Вычислив среднее между этим значением производной и её значением в начале интервала, найдём более точное значение yi+1: yi+1 = yi + h/2×[ f(xi,yi) + f(xi+1, y*i+1)].
Принцип метода проиллюстрирован на рис. 19.3. Для получения новой точки в нём требуется информация о двух других точках – предыдущей и промежуточной. Ошибка этого метода на каждом шаге имеет порядок h2.
Рис.19.3. Принцип модифицированного метода Эйлера Пример 2. Разработать, сохранить и выполнить программу для решения дифференциального уравнения из примера 1 модифицированным методом Эйлера. При выполнении расчетов использовать хранение результатов в массивах. Program ModEuler; Uses Crt; Var xn,xk,yn,yw,h:real; i,n:integer; x,y:array [1..20] of real;
Function f(x,y:real):real; begin f:=2*x*x+2*y; end;
Begin ClrScr; Writeln(' Решение дифференциального уравнения '); Writeln(' dy/dx=2x^2+2y модифицированным методом Эйлера '); xn:=0; yn:=1; xk:=1; h:=0.1; x[1]:=xn; y[1]:=yn; i:=1; repeat yw:=y[i]+h*f(x[i],y[i]); y[i+1]:=y[i]+h/2*(f(x[i],y[i])+f(x[i]+h,yw)); x[i+1]:=x[i]+h; i:=i+1; until x[i]>xk; n:=i; { Выводим результаты } Writeln('--------------------'); Writeln('| № | x | y |'); Writeln('--------------------'); for i:= 1 to n do Writeln('|', i:2, ' |', x[i]:5:2, ' |', y[i]:7:4, ' |'); Writeln('--------------------'); Readln; End. Метод Рунге-Кутта Для повышения точности вычисления значений функции требуется проведение дополнительных вычислений внутри интервала h, то есть между xi и xi+1. Метод Рунге-Кутта даёт набор формул для расчёта координат внутренних точек, требуемых для достижения точности, то есть ошибки на каждом шаге, порядка h4. Расчёты при использовании этого метода производятся по формулам:
где k0=h×f(xi,yi), k1=h×f(xi+h/2, yi+k0/2), Метод Эйлера и его модификация по сути дела являются методами Рунге-Кутта первого и второго порядка соответственно. По сравнению с ними метод Рунге-Кутта обеспечивает более высокую точность, что позволяет увеличить шаг интегрирования h. Допустимая погрешность на шаге определяет его максимальную величину.
Пример 3. Приведём фрагмент программы для решения дифференциального уравнения из примера 1 методом Рунге-Кутта. Program Runge; Uses Crt; Var xn,xk,yn,h,k0,k1,k2,k3:real; i,n:integer; x,y:array [1..20] of real;
Function f(x,y:real):real; begin f:=2*x*x+2*y; end;
Begin ClrScr; Writeln(' Решение дифференциального уравнения '); Writeln(' dy/dx=2x^2+2y методом Рунге-Кутта '); xn:=0; yn:=1; xk:=1; h:=0.1; x[1]:=xn; y[1]:=yn; i:=1; repeat k0:=h*f(x[i],y[i]); k1:=h*f(x[i]+h/2,y[i]+k0/2); k2:=h*f(x[i]+h/2,y[i]+k1/2); k3:=h*f(x[i]+h,y[i]+k2); y[i+1]:=y[i]+(k0+2*k1+2*k2+k3)/6; x[i+1]:=x[i]+h; i:=i+1; until x[i]>xk; n:=i; Writeln('----------------------'); Writeln('| № | x | y |'); Writeln('----------------------'); for i:= 1 to n do Writeln('|', i:2, ' |', x[i]:5:2, ' |', y[i]:7:4, ' |'); Writeln('----------------------'); Readln; End. Задание Дать сравнительную оценку результатов решения дифференциального уравнения из примера 1 y¢=2x2+2y при начальном условии y(0)=1; 0£ x£1 и h=0,1 обычным и модифицированным методами Эйлера и методом Рунге-Кутта. Для проверки использовать точное решение этого уравнения y=1,5×e2x-x2-x-0,5. Составить программу, выполняющую вычисления с использованием массивов. Результаты расчёта представить в виде таблицы, и вывести её на экран и принтер.
ОГЛАВЛЕНИЕ
ЛИТЕРАТУРА 1. Вычислительная техника и программирование. Практикум по программированию: Практ. пособие. / В.Е. Алексеев, А.С. Ваулин, Г.Б, Петрова; под ред. А.В. Петрова. – М.: Высшая школа, 1991. – 400с. 2. Немнюгин С.А. Turbo Pascal: Учебник. СПб.: Питер, 2001. –496с. 3. Немнюгин С.А. Turbo Pascal: практикум. СПб.: Питер, 2001. –256с. 4. Культин Н.Turbo Pascal 7.0. –СПб.: ВНV –Санкт-Петербург, 1998. –336 с. 5. Вальвачёв А.Н., Крисевич В.С. Программирование на языке Паскаль для персональных ЭВМ ЕС: Справ. пособие. –Мн.: Выш. шк. 1989. –223с. 6. Валвьачёв А.Н. Графическое программирование на языке Паскаль: справ. Пособие. –Мн.: Выш. шк. 1992. –143 с. 7. Программирование на персональных ЭВМ: Практикум: Учеб. пособие / Д.В. Офицеров, А.Б. Долгий, В.А. Старых; под ред. Д.В. Офицерова. –Минск: Высшая школа, 1993. –256с. 8. Программирование на языке TURBO PASCAL. / Учебн. Пособие под ред. Б.С. Богумирского и А.Д. Хомоненко. – СПб.: ВИККА им. А.Ф. Можайского, 1994. –326с. 9. Т.Шуп. Решение инженерных задач на ЭВМ: Практическое руководство. Пер. с англ. –М.: Мир, 1982. –238с.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.127.230 (0.009 с.) |

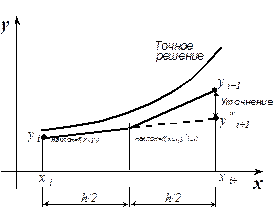
 ,
,


