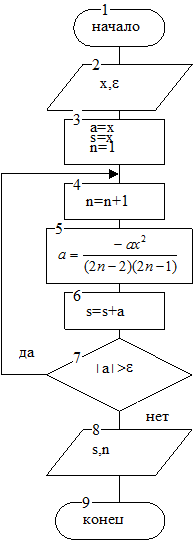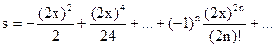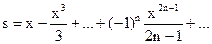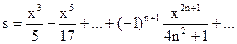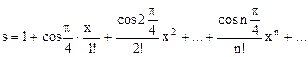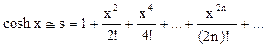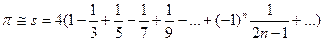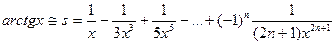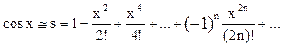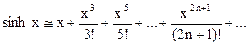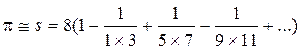Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмы и способы их описанияСодержание книги
Поиск на нашем сайте
ТЕМА 1 ТЕМА 2 Этапы подготовки и решения задач на ЭВМ На ЭВМ могут решаться задачи различного характера, например: научно-инженерные; разработки системного программного обеспечения; обучения; управления производственными процессами и т.д. В процессе подготовки и решения на ЭВМ научно-инженерных задач можно выделить следующие этапы: · постановка задачи; · математическое описание задачи (формализация); · выбор и обоснование метода решения; · алгоритмизация вычислительного процесса; · составление программы; · решение задачи на ЭВМ и анализ результатов. В задачах другого класса некоторые этапы могут отсутствовать, например, в задачах разработки системного программного обеспечения отсутствует математическое описание. Перечисленные этапы связаны друг с другом, а в некоторых случаях связь может быть настолько тесной, что разделение их становится затруднительным. Постановка задачи. На данном этапе формулируется цель решения задачи и подробно описывается её содержание. Анализируются характер и сущность всех величин, используемых в задаче, и определяются условия, при которых она решается. При этом важным моментом является корректность постановки задачи. Математическое описание задачи. На этом этапе производится математическая формализация задачи, то есть существующие соотношения между величинами, определяющими результат, выражаются в виде математических формул. Таким образом, формируется математическая модель явления, с указанием требуемой точности, допущениями и ограничениями. При этом, в зависимости от специфики решаемой задачи, могут быть использованы различные разделы математики и других дисциплин. Выбор и обоснование метода решения. Модель решения задачи с учётом её особенностей должна быть решена при помощи конкретных методов решения. Само по себе математическое описание задачи в большинстве случаев трудно перевести на язык машины. Выбор и использование метода решения задачи позволяет привести решение задачи к конкретным вычислительным операциям. При обосновании метода необходимо учитывать различные факторы и условия, в том числе, точность вычисления, время решения на ЭВМ, требуемый объём памяти, и другие. Одну и ту же задачу можно решить различными методами, при этом в рамках каждого метода можно составить различные алгоритмы.
Алгоритмизация вычислительного процесса. На данном этапе составляется алгоритм решения задачи согласно действиям, задаваемым выбранным методом решения. Процесс обработки данных разбивается на отдельные относительно самостоятельные блоки, и устанавливается последовательность выполнения блоков. Разрабатывается блок-схема алгоритма. Составление программы. При составлении программы алгоритм решения задачи переводится на конкретный язык программирования. Для программирования обычно используются языки высокого уровня, поэтому составленная программа требует перевода её на машинный язык. Этот процесс называется компиляция. В результате компиляции получается программа, полностью готовая к выполнению на ЭВМ, которая обычно хранится на магнитном носителе в виде исполняемого exe -файла и, иногда, набора вспомогательных файлов (с настройками, данными, шаблонами и пр.). Отладка программы. Отладка заключается в поиске и устранении синтаксических и логических ошибок в программе. В ходе синтаксического контроля программы компилятором выявляются команды и сочетания символов, недопустимые с точки зрения правил их построения или написания, принятых в данном языке. Используемая система программирования выдаёт программисту сообщения об ошибках, при этом вид и форма сообщений зависят от вида языка и версии используемой системы программирования. После устранения синтаксических ошибок программа становится работоспособной, то есть может быть выполнена на ЭВМ. Однако, это ещё не гарантирует того, что результаты, полученные при работе программы, будут правильными, поскольку могут остаться логические ошибки. Для их устранения проверяется логика работы программы в процессе её выполнения с конкретными исходными данными. При этом используются специальные методы, например, в программе выбираются контрольные точки, для которых вручную рассчитываются промежуточные результаты. Эти величины сверяются со значениями, получаемыми при выполнении на ЭВМ отлаживаемой программы. Кроме этого, для поиска ошибок могут быть использованы специальные отладчики, выполняющие специальные действия на этапе отладки, например, пошаговое выполнение программы с просмотром значений переменных, изменение значений переменных и др.
Решение задачи на ЭВМ и анализ результатов. После отладки программы её можно использовать для решения прикладной задачи. При этом обычно выполняется многократное решение задачи на ЭВМ для различных наборов исходных данных. Получаемые результаты интерпретируются и анализируются специалистом или пользователем, поставившим задачу. Разработанная программа длительного использования устанавливается на ЭВМ, как правило, в виде исполняемого exe -файла. К программе прилагается документация, включая инструкцию для пользователя. Все используемые в настоящее время языки программирования можно отнести к одному из следующих стилей: · процедурный; · функциональный; · логический; · объектно-ориентированный. Наибольшее распространение получили языки программирования, относящиеся к процедурному стилю. Процедурное программирование является отражением архитектуры традиционных ЭВМ, которая была предложена фон Нейманом в 40-х годах. Теоретической моделью процедурного программирования служит алгоритмическая система под названием «машина Тьюринга». Программа на процедурном языке программирования состоит из последовательности операторов (инструкций), задающих процедуру решения задачи. Основным является оператор присваивания, служащий для изменения содержимого областей памяти. Концепция памяти, как хранилища значений, содержимое которой может обновляться операторами программы, является фундаментальной в процедурном программировании. Выполнение программы сводится к последовательному выполнению операторов с целью преобразования исходного состояния памяти, то есть значений исходных данных, в заключительное, то есть в результаты. Таким образом, с точки зрения программиста, имеется программа и память, причём программа последовательно обновляет содержимое памяти. Процедурные языки характеризуются следующими особенностями: · необходимостью явного управления памятью, в частности, описанием переменных; · высокой эффективностью реализации на традиционных ЭВМ; · отсутствием строгой математической основы; · малой пригодностью для символьных вычислений. К языкам процедурного стиля программирования относятся Assembler (Ассемблер); С (Си); Basic (Бейсик); Fortran (Фортран); Pascal (Паскаль) и другие. Одним из наиболее популярных среди прикладных программистов процедурным языком программирования является Pascal, особенно для ПЭВМ. Разработанный в 1970 году швейцарским специалистом в области вычислительной техники профессором Никлаусом Виртом, язык назван в честь французского математика и по замыслу автора предназначался для обучению программированию. Однако, язык получился настолько удачным, что стал одним из основных инструментов прикладных и системных программистов при решении задач вычислительного и информационно-логического характера. В языке Pascal реализован ряд концепций, рассматриваемых как основа «дисциплинированного» программирования и заимствованных впоследствии разработчиками многих языков. Одним из существенных преимуществ языка Pascal является последовательная и достаточно полная реализация концепции структурного программирования. Это осуществляется не только путём упорядочивания связей между фрагментами программы по управлению, но и за счёт структуризации данных. Кроме того, в языке реализована концепция определения новых типов данных на основе уже имеющихся. Этот язык, в отличие от языка С, является строго типизированным. Pascal характеризуется
- высоким уровнем; - широкими возможностями; - стройностью, простотой, краткостью; - строгостью, способствующей написанию эффективных и надёжных программ; - высокой эффективностью реализации на ПЭВМ. Pascal реализован на ЭВМ различных типов, но наиболее распространён и развит для ПЭВМ. В настоящее время широко используются такие версии этого языка для ПЭВМ, как Turbo Pascal и Borland Pascal. После перехода на работу ПЭВМ под управлением Windows, версия этого языка Object Pascal, реализована в среде визуального программирования Delphi.
ТЕМА 3 Задание 1 Написать текст программы N1 в окне редактора системы Turbo Pascal, сохранить его в своем каталоге в файле с именем Progr1.pas, выполнить компиляцию и запустить программу в работу.
Задание 2 Написать текст программы N2 в системе Turbo Pascal: Uses Crt; Var s: string; Begin Write(’Как Вас зовут? ’); Readln(s); Writeln(’Привет, ’, s) End. Сохранить текст программы в своем каталоге в файле с именем Progr2.pas, выполнить компиляцию и запустить программу в работу. При выполнении программы от пользователя потребуется ввести с клавиатуры своё имя и нажать клавишу ENTER. Результаты работы программы просмотреть нажатием горячих клавиш Alt+F5. Задать режим компиляции программы «На диск» – пункт Destination Disk раздела Compile главного меню. Выполнить компиляцию (горячие клавиши Ctrl-F9). После этого задать компиляцию последующих программ в памяти (Destination Memory). Выйти из системы Turbo Pascal, найти в своей папке исполняемую программу Progr2.exe и проверить ее работу из операционной системы Windows.
Задание 3 Написать текст программы N3 в окне редактора Turbo Pascal: Uses Crt; Var x, y, z: real; Begin Write(’ x = ’); Readln(x); Write(’ y = ’); Readln(y); Z:= x + y; Writeln(’ z = ’, z:10:2) End. Сохранить текст в своем каталоге в файле с именем Progr3.pas, выполнить компиляцию и пошаговое прохождение программы, для чего воспользоваться командой Trace into раздела меню Run (выполнение программы построчно с заходом во все процедуры пользователя). При многократном использовании этой команды следует пользоваться горячей клавишей – F7. Проследить в окне пользователя порядок выполнения строк программы.
В программе можно использовать комментарии – пояснительный текст, ограниченный символами { } или (* *). Комментарий игнорируется компилятором и поэтому не оказывают влияния на выполнение программы. Обычно комментарии используют для пояснений смысла идентификаторов, операторов или частей программы. Задание 4 Дополнить текст программы N3 операторами очистки экрана и задания цветов фона и текста, после чего выполнить программу. Uses Crt; {использовать модуль CRT} Var x, y, z: real; Begin TextColor(Yellow); {цвет символов - желтый} TextBackground(Red); ClrScr; {очистить экран красным цветом} Write(’ x = ’); Readln(x); Write(’ y = ’); Readln(y); Z:= x + y; Writeln(’ z = ’, z:10:2) End. Тема 4 Упражнение 1. Ввести текст программы, выполняющей расчёт площади круга по известному значению радиуса. В программе используется стандартная константа pi, для выражения числа p=3,1415….
Данная программа, с точки зрения языка PASCAL является синтаксически и логически правильной, обеспечивая правильный результат расчёта. Однако интерфейс программы нельзя считать удовлетворительным. Для обеспечения удобства выполнения расчётов программа должна выводить сообщения о своём назначении, давать инструкции по вводу данных, и пояснения к результатам расчетов. Следующий вариант той же программы демонстрирует простые способы улучшения интерфейса.
Program Krug; Uses Crt; Var r,s:real;
Begin ClrScr; { очищаем экран } WriteLn(’Программа для вычисления площади круга’); { выводим информационные сообщения } WriteLn(’Введите исходные данные’); Write(’Введите величину радиуса, см R = ’); Readln(r); { вводим значение r } s:=pi*r*r; { выполняем расчет значения s } WriteLn(’Результаты расчетов’); { выводим результаты с точностью 2 десятичных знака } WriteLn(’Площадь круга с радиусом ’,r:8:2, ’ см равна ’, { организуем задержку выполнения программы до нажатия ENTER } Readln; End.
Результаты работы программы будут отображены в окне пользователя и останутся на экране, пока пользователь не нажмет клавишу ENTER.
Задания
1. Организовать ввод значений переменных: t – действительного типа; m и n - целого типа; ch – символьного типа; st – строки, длиной 15 символов. Сделать пояснения на экране для пользователя. Вывести значения этих переменных в одну строку, через два пробела, в следующем порядке: st, m, t, ch, n. Для t вывести 3 десятичных знака. 2. Вывести значения этих переменных в один столбец, выровненный по левому краю, в следующем порядке: n, ch, m, st, t. 3. Вывести значения этих переменных в один столбец, выровненный по правому краю. Правый край должен быть расположен в 15-й позиции строки. Переменные вывести в следующем порядке: n, ch, m, st, t.
4. Вывести 5 раз значение переменной t в столбец, выровненный по правому краю, количество десятичных знаков должно быть равно номеру строки. 5. Вывести в одну строку значения переменной t в трёх разных вариантах формата вывода действительных переменны, через 5 пробелов друг от друга. 6. Вывести 5 раз значение переменной ch в одну строку, с постепенным увеличением количества пробелов между значениями. 7. Вывести значения переменной n в центр 5-й строки и m в центр 8-й строки; 8. Вывести на экран горизонтальную линию на всю ширину экрана из знаков ‘-‘ (минус). 9. Вывести на экран пустую таблицу, состоящую из 4-х столбцов, шириной 10 знаков и 5 строк. Для изображения линий таблицы использовать знаки ‘-‘ (минус), ‘|‘ (вертикальная черта), ‘+‘ (плюс). 10. Вывести результат сравнения величин m и n. 11. Пронумеровать строки на экране. 12. Написать программу, которая для заданного целого числа a (2 £ a £ 10) выводит следующую таблицу a a a2 a a2 a3 a a2 a3 a4 Тема 5 Сложные выражения Выражение состоит из операндов и операторов. Операндами выражений могут быть константы и переменные. Операторы находятся между операндами и обозначают действия, выполняемые над операндами. Значения переменных должны быть определены до их появления в арифметическом выражении. В табл.3.1 перечислены операторы и математические функции, используемые в арифметических выражениях Turbo Pascal. При записи выражений между операндом и оператором, за исключением операторов div и mod, пробел можно не ставить. Операторы имеют разный приоритет. Наивысший приоритет имеют функции, далее – умножение и деление, наименьший – сложение и вычитание. Приоритет операторов влияет на порядок их выполнения. При вычислении выражения сначала выполняются операторы с более высоким приоритетом. Если приоритет операторов в выражениях одинаковый, то сначала выполняется тот оператор, который находится левее. Выражение записывается в одну строку. Порядок вычислений можно изменить с использованием круглых скобок: Y:=(R*T+25)/(a*(b+c*(d+f*(x+g)))); При записи выражений, содержащих скобки, должна соблюдаться парность скобок, т.е. число открывающих скобок должно быть равно числу закрывающих скобок. При записи сложных выражений можно использовать вспомогательные переменные для хранения результатов промежуточных вычислений. Это позволяет проконтролировать результаты промежуточных вычислений. Таблица 3.1. Операторы и математические функции языка Turbo Pascal
Как видно из таблицы, в языке Turbo Pascal отсутствуют следующие математические выражения: y=lg x; y=ax; y=tg x. Для вычисления этих величин можно использовать выражения: y:=ln(x)/ln(10); y:=EXP(x*ln(a)); y:=sin(x)/cos(x) соответственно. Аргумент для тригонометрических функций задаётся в радианах. Для пересчёта из градусов в радианы используется соотношение Радианы = градусы ´ (p ¤ 180) Например, чтобы вычислить sin 45° надо записать sin(45*pi/180). Задание Составьте программу для вычисления следующих выражений:
При выполнении программы использовать предлагаемые значения переменных a, b и c. При правильно составленном выражении результат должен совпасть со значением, приведённым в последней колонке. Тема 6 Задание 1 Составьте программу для вычисления следующих выражений. Программа должна обеспечить ввод значений Х, расчет и вывод значений Y.
Задание 2 Составьте программу, которая бы выводила на экран сообщение о количестве занятий, в зависимости от дня недели (понедельник = 1, вторник = 2 и т.д.), цифровое обозначение которого ввести с клавиатуры, с применением оператора case. Тема 7 Задание Разработать программу для расчета и вывода таблицы значений функции, состоящей из n строк, в соответствии с вариантом задания, при изменении аргумента от начального и с заданным шагом Dx (см. табл.). Ввод исходных данных организовать с помощью присваивания значений переменным.
Тема 8 Задания При выполнении заданий в учебных целях следует организовывать циклы в задании 1 при помощи оператора while, в задании 2 - при помощи оператора repeat. Вариант 1 Задание 1. Найти t, при котором значение выражения (2+4+6+…+2t)/(1×2×3×…×t) становится меньше 0,06. Задание 2. Из пункта А в пункт В, расстояние между которыми 500 км, равномерно и прямолинейно движется автомобиль со скоростью v. При вводе v с клавиатуры вывести на экран в одну строку через один пробел расстояния от автомобиля до пункта В через каждые два часа от начала движения до момента прибытия в пункт В. Вариант 2 Задание 1. Найти x, при котором значение выражения (0,5×1×1,5×2×…×0,5x)/x2 становится больше s при вводе s с клавиатуры. Задание 2. Из пункта А в пункт В, расстояние между которыми s км, равномерно и прямолинейно движется материальная точка со скоростью v. При вводе v и s с клавиатуры вывести на экран в один столбец расстояния от материальной точки до пункта А через каждый час от начала движения до момента прибытия в пункт В. Вариант 3 Задание 1. Найти f, при котором значение выражения (f3+ln f)/(f2-11f+2,3) становится больше s при вводе s с клавиатуры, если f увеличивается в ряду 1,2,3,4, …. Задание 2. Материальная точка равноускоренно и прямолинейно движется с начальной нулевой скоростью и ускорением a км/мин2. Скорость точки описывается уравнением v=at, где t - время. При вводе a с клавиатуры вывести на экран в один столбец значения скорости точки через каждую минуту от начала движения до момента достижения скорости 20 км/мин. Вариант 4 Задание 1. Найти значение выражения 1+3+5+7+…+(2z-1) при вводе z с клавиатуры. Задание 2. Камень падает с высоты 200 м. Без учета сопротивления воздуха длина пути, пройденного камнем, описывается уравнением s=gt2/2, где g - ускорение свободного падения, t - время. Вывести на экран в один столбец расстояния от камня до земли через каждую секунду от начала падения до момента соприкосновения с землей. Вариант 5 Задание 1. Найти значение выражения 1/1+1/2+1/3+1/4+…+1 / n при вводе n с клавиатуры. Задание 2. Скорость некоторой химической реакции при 0°С равна 0,002 моль/л×мин и увеличивается в два раза при увеличении температуры на каждые 10°С (температурный коэффициент реакции равен 2). Вывести на экран в два столбца значения температуры, начиная от 0°С, с шагом 10°С, и соответствующие им значения скорости реакции до достижения скорости более 0,2 моль/л×мин. Вариант 6 Задание 1. Найти значение выражения (1+2+3+4+…+n)/(2×4×6×…×2n) при вводе n с клавиатуры. Задание 2. Вывести на экран в одну строку через один пробел все високосные годы в период с 2000 до 2050, при условии, что 2000-й год - високосный. Вариант 7 Задание 1. Найти j, при котором значение выражения (lg j+134j)/(j2-ln j+3) становится меньше e при вводе e с клавиатуры, если j увеличивается в ряду 1,2,3,4, …. Задание 2. Вывести на экран в три столбца массовые концентрации серной кислоты в растворе при возрастании от 10 г/л до 300 г/л с шагом 10 г/л, а также соответствующие им молярные концентрации (моль/л) и нормальные концентрации (г-экв/л). Вариант 8 Задание 1. Найти x, при котором значение выражения 100+99+98+97+…+x становится меньше r. Значение r ввести с клавиатуры (r<100). Задание 2. Вывести на экран в четыре столбца значения длин в метрах в диапазоне от 1 до 20 м с шагом 1 м, а также соответствующие им значения длин в дюймах (в одном дюйме 2,54 см), футах (в одном футе 0,3048 м) и ярдах (в одном ярде 0,9144 м). Вариант 9 Задание 1. Найти значение выражения 1+4+9+16+…+x2 при вводе x с клавиатуры (x - целое число). Задание 2. Вывести на экран в четыре столбца значения объема в литрах при убывании от 40 до 2 л с шагом 2 л, а также соответствующие им значения объема в галлонах (в одном галлоне 4,546 л), квартах (в одной кварте 1,138 л) и пинтах (в одной пинте 0,569 л). Вариант 10 Задание 1. Найти сумму квадратных корней первых ста натуральных чисел. Задание 2. Растворимость сернистого газа в воде описывается уравнением x=0,3p×1,0363-t, где x - растворимость, г/л, p - парциальное давление сернистого газа, мм.рт.ст., t - температура, °С. Вывести на экран в два столбца значения температуры в диапазоне от 0 до 50°С с шагом 5°С и соответствующие им значения растворимости сернистого газа при вводе p с клавиатуры. Тема 9 Итерационные алгоритмы циклической структуры
Итерационные алгоритмы нашли широкое применение в инженерно-технических расчётах. В этих расчётах производится многократные последовательные вычисления с целью постепенного приближения к искомому результату, причем для вычислений на каждом шаге используются результаты вычислений на предыдущем шаге. Завершение вычислений производится при достижении заданной точности вычислений. Поскольку количество итераций (повторений вычислений) заранее неизвестно, то при организации вычислений необходимо использовать циклы While или Repeat. Итерационные алгоритмы применяются, например, в задачах вычисления суммы ряда или величины его членов, при численном решении нелинейных уравнений, и т.п. Одной из наиболее часто используемых областей использования итерационных алгоритмов является вычисление значений тригонометрических и трансцендентных функций, таких, как синус, косинус, натуральный логарифм, экспонента и др. При этом, задаваясь требуемой точностью вычислений, можно заменить точное значение функции, например, sin x, её приближённым значением, полученным в результате сохранения конечного числа членов разложения этой функции в ряд Тейлора:
Точность конечного результата зависит от количества сохранённых членов ряда. Если задана погрешность e (и, например, равна 10-4). Номер последнего слагаемого n определяется условием Упражнение. Вычислить на ЭВМ значение суммы членов бесконечного ряда Ключевым этапом решения задачи является вычисление каждого члена ряда
Блок-схема алгоритма решения представлена на рис. 7.1. В блоке 2 организуется ввод исходных данных. В блоке 3 производится подготовка цикла, для этого задаётся значение первого члена ряда, начальное значение суммы, равное этому члену, и номер члена ряда, равный 1 (просуммирован один член). Блоки 4 и 5 выполняют расчет текущего номера члена ряда и значения этого члена с использованием рекуррентного соотношения. Блок 6 реализует функцию накопления суммы. Блок 7 выполняет проверку условия окончания цикла. В блоке 8 организуется вывод результатов расчётов.
Задание Вычислить на ЭВМ значение суммы членов бесконечного ряда с заданной точностью e. На печать вывести значение суммы и число членов ряда, вошедших в сумму.
Тема 10 Работа с массивами По определению, принятому в языке Pascal, массив - это сложный тип данных, состоящий из фиксированного числа элементов, имеющих один и тот же тип. С точки зрения программиста массив – это группа однотипных переменных с одним именем, каждый элемент массива имеет свой номер (индекс). Массив описывается одним из следующих способов: 1) Var identificator: array [ index-type ] of element-type; 2) Type TypeName= array [ index-type ] of element-type; Var identificator: TypeName; Тип элементов может быть любым, но индекс должен быть перечислимого типа. Примеры описаний типа массив: IntList:array[1..100] of Integer; CharData:array['A'..'Z'] of Byte; Matrix:array[0..9, 0..9] of Real; Если в описании массива задан один индекс, массив называется одномерным, если два индекса – двухмерным, если n индексов – n -мерным. Одномерные массивы обычно используются для представления векторов, а двумерные – для представления матриц. После объявления массива к каждому его элементу можно обратиться, указав идентификатор (имя) массива и индекс (номер) элемента в квадратных скобках. Например, запись IntList[2] позволяет обратиться ко второму элементу массива IntList, а запись Matrix[4,5] делает доступным для использования значение элемента, находящегося в четвёртом столбце пятой строки массива Matrix. Перед использованием массива рекомендуется его очистить путём присваивания каждому элементу массива значения нуль: for i:=1 to n do a[i]:=0; Заполнение массива, то есть присваивание элементам массива значений может производиться путём ввода данных с клавиатуры, генерации случайных чисел, или присваивания результатов вычисления выражений. Пример 1. Ввод с клавиатуры 10 элементов массива. for i:=1 to 10 do begin Write(i,'-й элемент массива = '); Readln(a[i]); end; Пример 2. Генерация массива действительных случайных чисел в диапазоне от X до Y: for i:=1 to n do a[i]:=x+(y-x)*random; (перед использованием функции random следует выполнить ее инициализацию функцией randomize) Пример 3. Вывод массива из 10 элементов действительного типа Writeln('Вывод элементов массива в строку:'); for i:=1 to 10 do Write(a[i]:7:2); Writeln('Вывод элементов массива в столбец:'); for i:=1 to 10 do Writeln(i,'-й элеме
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.179.209 (0.011 с.) |




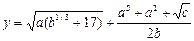


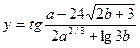
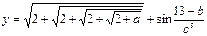
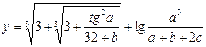
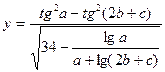
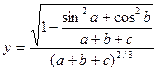



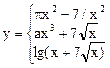
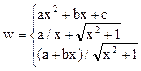



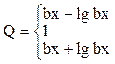



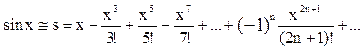
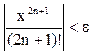
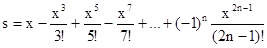 точностью до члена ряда, меньшего e = 10-4 для x, равного 0,1. Определить число членов ряда, вошедших в сумму.
точностью до члена ряда, меньшего e = 10-4 для x, равного 0,1. Определить число членов ряда, вошедших в сумму.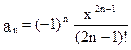 . Его значение можно вычислять напрямую, однако, удобнее выразить n -й член через (n-1) -й, в данном случае получаем:
. Его значение можно вычислять напрямую, однако, удобнее выразить n -й член через (n-1) -й, в данном случае получаем: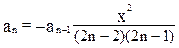 . Такие алгоритмы и формулы, в которых на каждом шаге используются значения, вычисленные на предыдущем шаге, называются рекуррентными.
. Такие алгоритмы и формулы, в которых на каждом шаге используются значения, вычисленные на предыдущем шаге, называются рекуррентными.