
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмы построения графика аналитически заданной функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При выводе на экран графических изображений используется графическая система координат. Графические координаты задают положение каждого пиксела, отображаемого на экране. В отличие от обычной (декартовой) системы координат, графические координаты принимают только целочисленные значения. Диапазон изменения графических координат ограничен снизу нулём, а сверху разрешением экрана по горизонтали и вертикали. Максимальное значение x и y -координат можно получить, используя функции GetMaxX и GetMaxY. Графическая координата y отсчитывается сверху вниз. Геометрические декартовы координаты точки (x,y) для её изображения на экране необходимо пересчитать в графические (xg,yg) по формулам:
где x0, y0 – смещение изображения на экране от левого края и сверху; yG – разрешение экрана по вертикали; dx и dy – размер собственно изображения по горизонтали и вертикали соответственно; xmin, ymin, xmax, ymax – минимальные и максимальные значения аргумента x и значения функции y в диапазоне построения графика; ë a û - целая часть числа a. Таким образом, для построения графика функции необходимо: - получить таблицу значений функции y = f(x) в диапазоне изменения x от xнач до xкон; - найти минимальные и максимальные значения аргумента x и значения функции y в диапазоне построения графика; - пересчитать действительные значения x и y в графические xg и yg; - нарисовать на экране область построения графика и оси координат; - отправить графический указатель (перо) в начало координат; - задать цвет и стиль линий; - последовательно соединить линиями (или отметить маркерами) точки графика. При построении нескольких графиков на одном координатном поле необходимо определить максимальные и минимальные значения x и y для всех графиков. Рассмотрим пример использования графического режима для построения графика функции y = sin x. В примере используется 3 подпрограммы-функции f, xe и уe, причём xe и уe вызываются без параметров. Program Prg_graf; Uses Crt, Graph; Var xn, xk, x, y, Ymin, Ymax, dx:real; MX, MY,i, n: word; Gd, Gm: integer;
Function f(xf:real):real; { расчет функции } begin f:=sin(xf); { Здесь приводим выражение для вычисления } {или f:=exp(-0.5*xf*xf);} { значения Вашей функции } end;
Function Xe:word; {расчет позиции на экране для X} begin Xe:=10+Round((MX-20)*(x-xn)/(xk-xn)); end;
Function Ye:word; { расчет позиции на экране для Y } begin { на экране отсчет идет сверху-вниз } { на обычном графике – наоборот } Ye:=MY-10-Round((MY-20)*(f(x)-Ymin)/(Ymax-Ymin)); end;
Begin { Начало основной программы } xn:=-5; xk:=5; n:=250; { Исходные данные } Write(' x начальное = '); Readln(xn); Write(' x конечное = '); Readln(xk); Write(' количество точек графика = '); Readln(n); } dx:=(xk-xn)/(n-1); { интервал между точками на оси Х } { Нахождение минимума и максимума функции } x:=xn; Ymin:=f(xn); Ymax:=f(xn); for i:=2 to n do begin x:=x+dx; if f(x)<Ymin then Ymin:=f(x); if f(x)>Ymax then Ymax:=f(x); end; Gd:=Detect; InitGraph(Gd,Gm,''); { не забудьте скопировать egavga.bgi } { в папку с программой Prg_graf.pas } if GraphResult <> 0 then begin Writeln('Ошибка инициализации графического режима'); Halt(1); end; MX:=GetMaxX; MY:=GetMaxY; Rectangle(0,0,MX,MY); { Рамка вокруг всего экрана } Rectangle(10,10,MX-10,MY-10); { Рамка вокруг поля графика } OutTextXY(270,2,'График функции'); { Вывод строки } x:=0; Line(Xe,MY-10,Xe,10); { Рисуем ось ординат для x=0} OutTextXY(Xe-10,15,'Y'); { Подписываем ось ординат } y:=0; Line(10,MY-Ye,MX-10,MY-Ye);{ Рисуем ось абсцисс для y=0} OutTextXY(MX-20,MY-Ye+2,'X'); { Подписываем ось абсцисс } OutTextXY(Xe-10,MY-Ye+2,'0'); {Подписываем начало координат} { Рисуем сам график } x:=xn; MoveTo(Xe, Ye); { Перемещаем перо в начало координат } for i:=2 to n do begin x:=x+dx; LineTo(Xe,Ye); { Чертим линию до следующей точки} end; Readln; CloseGraph; End. Задание 1. Ввести текст программы Prg_graf с клавиатуры в системе Turbo Pascal и сохранить в свою папку. 2. Выполнить отладку программы. 3. Пользуясь программой построить графики для следующих функций: 1) y = exp(- a×x2); 2) y = x /(sin(5x) + 1,5); 3) y = a× x2 + b×x + c; 4) y = ± 5) E = 1010 / 6) y = 2x; 7) y =|cos(x)|; 8) y = x/(1 - x2); 9) y = ± x 10) y = 0,1×x×sin(x/0,5)
Тема 16 Анимация изображений Общим принципом создания движущихся изображений является рисование какого-либо объекта, закраска его цветом фона (стирание) и последующее рисование уже с новыми координатами. При этом необходимо отметить, что эффект движения возникает не всегда. Если частота появления картинки на экране мала, то наблюдается перемещение мигающего объекта. Если объект перемещается слишком быстро, то человеческий глаз не способен воспринять всей траектории движения. На восприятие еще накладывается частота обновления кадра монитора. Может возникать ситуация, когда мерцание наблюдается по этой причине. Продолжительность нахождения на экране прорисованного объекта должна быть максимальна, а продолжительность нахождения стертого минимальна. Ниже приведена программа, в которой организовано перемещение по экрану окружности. В данном случае частоту обновления изображения можно регулировать варьированием продолжительности задержки (time) и величины перемещения (delta), а также размером объекта - переменная radius (чем меньше радиус окружности, тем меньше времени необходимо на ее прорисовку). Перед выполнением примера скопируйте в свой каталог драйвер egavga.bgi; Program Multik; Uses Graph, Crt; Var x,y,dy,dx,time,delta,radius,Gd,Gm: integer; Begin Gd:= Detect; InitGraph(Gd,Gm,''); {Включаем графический режим} if GraphResult <> grOk then Halt(1); Rectangle(0,0,GetMaxX,GetMaxY); {рисуем рамку вокруг экрана} x:=100; y:=100; { начальные координаты центра окружности} delta:=10; { величина перемещения } dx:=delta; { величина перемещения по х } dy:=delta; { величина перемещения по у } radius:=15; { радиус окружности } time:=10000; { продолжительность задержки } Repeat SetColor(15); { задание белого цвета для линий } Circle(x,y,radius);{ рисование белой окружности} { смена направления движения при достижении края экрана } { и включение звукового сигнала } if y>=GetMaxY-radius then { нижний край } begin dy:=-delta; Sound(2000); end; if y<=radius then { верхний край } begin dy:= delta; Sound(3000); end; if x>=GetMaxX-radius then { правый край } begin dx:=-delta; Sound(5000); end; if x<=radius then { левый край } begin dx:= delta; Sound(4000); end; Delay(time); { задержка выполнения программы } NoSound; SetColor(0); { задание черного цвета } Circle(x,y,radius); { рисование черной окружности } x:=x+dx; y:=y+dy; { расчёт новых координат } { выход из программы при нажатии любой клавиши } Until KeyPressed; CloseGraph; { Выход из графического режима } End. Следующая программа рисует окружности, координаты которых, радиус и цвет определяются значениями функции синуса или косинуса. Параметры синусоид задаются случайными числами, поэтому образующаяся на экране фигура каждый раз будет отличаться от предыдущих. В первом цикле for присходит прорисовка 200 окружностей различными цветами, а во втором закраска их черным цветом. Внутри первого цикла организована задержка с помощью процедуры delay, для того чтобы между прорисовкой окружностей проходило некоторое время. Также задержка поставлена перед затиранием фигуры черным цветом. Завершение работы программы произойдет при нажатии любой клавиши. Program Salut; Uses Graph, Crt; Var n,y,x,a,b,c,f,e,i,Gd,Gm: integer; Begin Randomize; { Инициируем генератор случайных чисел } Gd:= Detect; InitGraph(Gd,Gm,''); {Включаем графический режим} if GraphResult <> grOk then Halt(1); y:=round(GetMaxY/2); { координаты центра экрана } x:=round(GetMaxX/2); n:=200; { количество повторов } c:=50; Repeat a:=random(c)+10; b:=random(c)+10; e:=5+random(20); f:=random(120); for i:=1 to n do begin Delay(50); SetColor(round(i/10)+1); Circle(round((y-i/e)*sin(i/a))+x, round((y/2-i/e)*cos(i/b))+y, f-round(c*sin(i/e))); end; delay(65535); for i:=1 to n do begin SetColor(0); Circle(round((y-i/e)*sin(i/a))+x, round((y/2-i/e)*cos(i/b))+y, f-round(c*sin(i/e))); end; Until KeyPressed; CloseGraph; End. Задание 1 a) Наберите программу Multik и измените скорость перемещения окружности с помощью варьируемых параметров так, чтобы окружность плавно перемещалась. б) Организуйте движение второй окружности с независимыми от первой параметрами. Задание 2 а) Наберите программу Salut и модифицируйте ее так, чтобы вместо окружности перемещался бы эллипс, все параметры которого также зависели бы от случайных чисел. б) Модифицируйте программу так, чтобы вместо эллипса перемещалась бы прямая, координаты и цвет которой зависели бы также от случайных чисел. Тема 17 Численные методы вычисления определённого интеграла При решении инженерных задач часто приходится вычислять значения определённого интеграла. В случаях, когда не удаётся выразить интеграл в замкнутой форме, или полученная формула сложна, или подынтегральная функция задана таблично, пользуются численным интегрированием. В основе численного интегрирования лежит приближенное вычисление площади под кривой, описываемой подынтегральной функцией. В общем виде задача формулируется как нахождение значения
Наиболее простыми для реализации являются методы, для которых значения x заданы с постоянным шагом. Мы рассмотрим методы прямоугольников, трапеций (Ньютона-Котеса) и парабол (Симпсона). В общем виде алгоритм решения задачи состоит из шагов: 1. Интервал, на котором выполняется интегрирование [a,b], разбивается на n равных отрезков и вычисляется длина этих отрезков; 2. Криволинейная трапеция S заменяется фигурой, составленных, в зависимости от метода, из элементарных прямоугольников, трапеций, или криволинейных трапеций; 3. Вычисляются и суммируются площади Si каждой элементарной фигуры. Метод прямоугольников Пусть на отрезке [a,b] задана непрерывная функция y=f(x), см. рис.17.1. Интервал, на котором выполняется интегрирование [a,b], разбивается на n равных отрезков, и криволинейная трапеция S заменяется фигурой, составленной из элементарных прямоугольников с площадями Si., рис.17.2.
Шаг интегрирования Площадь элементарной фигуры Интеграл равен
Таким образом, для вычисления определённого интеграла методом прямоугольников достаточно вычислить сумму значений подынтегральной функции в узлах интегрирования и умножить эту сумму на шаг интегрирования. Преимуществом метода является его простота, недостатком – сравнительно невысокая точность, для повышения которой необходимо увеличивать значение n до 1...10 тысяч. Пример 1. Составить программу для вычисления интеграла Program Integral1; Uses Crt; Var a,b,s,x,h:real; i, n: integer;
Function f(xx:real):real; begin f:=xx*xx; {Здесь приводим выражение для вычисления функции } end;
Begin ClrScr; Writeln(' Вычисление определенного интеграла'); Writeln(' Метод прямоугольников'); { Ввод исходных данных } a:=0; b:=3; n:=1000; { Начинаем расчет } h:=(b-a)/n; s:=0; x:=a; for i:=1 to n do begin x:=x+h; s:=s+f(x); end; s:=s*h; Writeln(' Интеграл равен ', s:10:7); Readln; End.
Метод трапеций Сущность интегрирования методом трапеций составляет кусочно-линейная аппроксимация подынтегральной функции. Соседние точки (xi,yi) и (xi+1,yi+1), заданные таблицей в интервале a£x£b, соединяются прямыми. Если x0=a, а xn=b, то интеграл будет представлять собой сумму площадей n трапеций высотой h каждая. На рис. 17.3 показан графически принцип метода трапеций.
Рис.17.3. Интегрирование методом трапеций
Расчётная формула получается следующим образом
Итоговая формула выглядит следующим образом
Таким образом, для вычисления определённого интеграла методом трапеций надо вычислить сумму значений подынтегральной функции в узлах интегрирования между a и b и умножить эту сумму на шаг интегрирования. К полученному значению прибавляется полусумма значений подынтегральной функции на концах отрезка, умноженная на шаг интегрирования. Совершенно очевидно, что чем меньше интервал, через которые задаётся значение функции, тем с большей точностью будет вычислен определённый интеграл. Метод Симпсона Повысить точность результат вычисления определённого интеграла можно, если заменить линейную аппроксимацию, используемую в методе трапеций, кусочной аппроксимацией кривыми, например, параболой второго порядка. Для проведения каждой параболы требуется три точки. Аппроксимируя подынтегральную функцию параболами, получаем формулу Симпсона:
В этой формуле число интервалов должно быть чётное. Таким образом, для вычисления определённого интеграла методом Симпсона надо вычислить отдельно суммы значений подынтегральной функции в узлах интегрирования между a и b в чётных и нечётных точках. Сумма, полученная для нечётных точек умножается на 4, а сумма для чётных точек - на 2. К полученным двум суммам прибавляется сумма значений подынтегральной функции на концах отрезка. Полученный итог умножается на 1/3 шага интегрирования. Все вышеприведённые алгоритмы вычисления определённого интеграла используется заданный шаг интегрирования. Кроме этого, существуют итерационные алгоритмы, в которых вычисления выполняются до заданной точности e результата. При каждой итерации количество узлов интегрирования n удваивается, а затем новый результат сравнивается с результатом, полученном на предыдущем шаге. Вычисления повторяются в цикле, пока разница между результатами не станет меньше e. Задания 1. Набрать текст программы Integral1. Провести вычисления и вывести на принтер (экран) результаты расчётов при n =10; 100; 1000; 10000. Сравнить точность и скорость вычислений. 2. Сохранить под другим именем и модифицировать программу, чтобы она вычисляла значение интеграла методом трапеций. Сравнить точность и скорость вычислений при n =10; 100; 1000; 10000. 3. Сохранить под другим именем и модифицировать программу, чтобы она вычисляла значение интеграла методом парабол. Сравнить точность и скорость вычислений при n =10; 100; 1000; 10000. 4. Сохранить под другим именем и используя три предыдущих примера модифицировать программу, чтобы она последовательно вычисляла значение интеграла методом прямоугольников, трапеций и парабол. Сравнить точность и скорость вычислений при n =10; 100; 1000; 10000. Для этого результаты должны выводиться в виде таблицы Результаты вычисления определённого интеграла методами
Варианты заданий
Тема 18 Численные методы решения нелинейных уравнений При решении инженерных задач встречаются алгебраические и трансцендентные уравнения, что может представлять собой самостоятельную задачу или являться составной частью более сложных задач. В обоих случаях применение численного метода позволяет быстро и эффективно добиться решения задачи. Линейные уравнения имеют одно решение, алгебраические уравнения – n решений, трансцендентные – неопределённое число решений. Решение линейных уравнений с одним неизвестным является достаточно простой задачей и здесь не рассматривается. Уравнения, содержащие только суммы целых степеней x, называются алгебраическими. Их общий вид Нелинейные уравнения, содержащие тригонометрические функции или другие специальные функции, например, lg x или ex, называются трансцендентными. Для решения нелинейных уравнений, для которых отсутствует аналитическое решение или оно очень сложно, применяют численные методы, в которых, как правило, применяются итерационные алгоритмы. В итерационных методах задаётся процедура решения в виде многократного применения некоторого алгоритма. Полученное решение всегда является приближённым, хотя может быть сколь угодно близким к точному. В общем случае задача формулируется следующим образом. Пусть на отрезке [a,b] дана непрерывная функция y=f(x), причем значения f(a) и f(b) имеют разные знаки. Тогда абсцисса точки пересечения графика функции y=f(x) с осью X будет корнем уравнения f(x)=0, см. рис.18.1. Другими словами, требуется найти такое значение x, при котором значение функции f(x) будет равно нулю.
Рис.18.1. Графическая интерпретация нахождения корня уравнения Численными методами значение корня определяется с погрешностью, не превосходящей данного положительного, достаточно малого числа e. Иначе говоря, если v – истинное значение корня, при котором f(v)=0, то требуется определить такое число w, при котором a£w£b и ½ v-w ½ <e. Первый этап решения состоит в отыскании области существования корня, т.е. отрезков на оси абсцисс, в концах которых функция имеет разные знаки. Для этого вычисляются значения функции в точках, расположенных через равные интервалы на оси x. Это делается до тех пор, пока не будут найдены два последовательных значения функции f(xn) и f(xn+1), имеющих противоположные знаки, т.е. f(xn)×f(xn+1)<0. Таким образом, при a= xn, b=xn+1, уточнение корней будет производиться на отрезке [a,b]. Для решения данной задачи применяются методы: половинного деления, касательных (Ньютона), хорд и секущих. Метод половинного деления Алгоритм метода состоит из следующих операций. Отрезок [a,b] делят пополам точкой c, c=(a+b)/2, и находят значение функции в точке с. Если f(c)=0, то корень уравнения соответствует точке c. Если f(c)¹0, то можно сузить диапазон поиска корня: перейти от отрезка [a,b] к отрезку [a,c] или [c,b] в зависимости от знака f(c). Если f(a)×f(c)<0, то корень находится на отрезке [a,c], и точку с будем считать точкой b; а если f(a)×f(c)>0, то корень находится на отрезке [c,b], и точку с будем считать точкой a. Каждый такой шаг уменьшает в два раза интервал, в котором находится корень уравнения f(x)=0. После нескольких шагов получится отрезок, длина которого будет меньше или равна числу e, т.е. ½ a-b ½ £e. Любая точка такого отрезка, например, один из его концов, подходит в качестве решения поставленной задачи. На рис. 18.2. показано несколько этапов применения алгоритма.
Рис.18.2. Графическая иллюстрация метода половинного деления: 1…5 – интервалы уточнения корней на 1..5 шаге алгоритма Пример 1. Найти с точностью e=0,001 на отрезке [-2,1] корень уравнения x3+x2+x+1=0. Приведём текст программы, которая решает эту задачу методом половинного деления. Результат выводится на экран, и, по желанию пользователя, на принтер. Program Popolam; Uses Crt, Printer; Var a,b,c,eps,a0,b0:real; k:integer; ch:char;
Function f(x:real):real; begin {Здесь приводим выражение для вычисления функции } f:=x*x*x+x*x+x+1; end;
Begin ClrScr; Writeln(' Решение уравнения методом половинного деления '); { Ввод исходных данных } a:=-2; b:=1; eps:=0.001; a0:=a; b0:=b; { запоминаем исходные данные } { Начинаем расчет } k:=0; { Счетчик повторений } While abs(b-a)>=eps do begin k:=k+1; c:=(a+b)/2; if f(a)*f(c)<=0 then b:=c else a:=c; end; Writeln(' Уравнение x^3+x^2+x+1=0 на отрезке [',a0:4:1, ',', Writeln(' f(x) = ',f(c):10:8); Writeln('Точность ',eps:10:8, ' достигнута за ', Write(' Печатать результаты на принтере? (Y/N)'); Repeat ch:=ReadKey; ch:= UpCase(ch); Until (ch='Y') or (ch='N'); if ch='Y' then begin Writeln(lst,'Решение уравнения методом половинного деления'); Writeln(lst,' Уравнение x^3+x^2+x+1=0 на отрезке [', Writeln(lst,' f(x) = ',f(c):10:8); Writeln(lst,' Точность ',eps:10:8, ' достигнута за ', Writeln('Печать выполнена. Нажмите ENTER '); Readln; end; End. Метод Ньютона В отличие от метода половинного деления, для определения интервала, в котором заключён корень, не требуется находить значения функции с противоположными знаками. Вместо интерполяции по двум значениям функции, в методе Ньютона осуществляется экстраполяция с помощью касательной к кривой в данной точке. В основе метода лежит разложение функции f(x) в ряд Тейлора
Члены ряда, содержащие h во второй и более высоких степенях, отбрасываются; используется соотношение xn+h=xn+1. Предполагается, что переход от xn к xn+1 приближает значение функции к нулю так, что f(xn+h)=0. Тогда xn+1=xn - f(xn)/ f`¢(xn). Значение xn+1 соответствует точке, в которой касательная к кривой в точке xn пересекает ось x. Так как кривая f(x) отлична от прямой, то значение функции f(xn+1) не будет в точности равно нулю. Поэтому вся процедура повторяется, причём вместо xn используется xn+1. Счет прекращается, когда разница между xn к xn+1 будет меньше или равна числу e, т.е. ½ xn- xn+1 ½ £e.
Рис. 18.3. процесс решения уравнения методом Ньютона На рис. 18.3. процесс решения уравнения методом Ньютона, который ёще называют методом касательных, показан графически. Пример 2. Приведём фрагменты текста программы, которая решает задачу из примера 1 методом касательных. Ввод и вывод результатов подробно разобран выше. Program Kasat; Uses Crt, Printer; Var a,b,t,x,eps:real;
Function f(x:real):real; begin {Здесь приводим выражение для вычисления функции } f:=x*x*x+x*x+x+1; end; Function f1(x:real):real; begin { Здесь приводим выражение для производной функции } f:=3*x*x+2*x+1; end;
Begin ClrScr; Writeln(' Решение уравнения методом касательных'); { Ввод исходных данных } a:=-2; b:=1; eps:=0.001; { Начинаем расчет } x:=a; Repeat t:=f(x)/f1(x); x:=x-t; Until abs(t)<=eps; Writeln(' Уравнение имеет корень x = ', x:10:8); Readln; End. Метод Ньютона требует меньшего числа повторений, чем метод половинного деления. Недостатки метода – необходимость дифференцирования функции f(x), и f(x) должно быть не равно нулю. Метод хорд Этот метод ещё имеет название метода ложного положения. В основе метода лежит линейная интерполяция по двум значениям функции f(x), имеющим противоположные знаки. Через точки, соединяющие значения функции f(a) и f(b) на концах отрезка [a,b], проводят прямую, которая пересекает ось x в точке
Значение функции f(x) сравнивается со значениями функций f(a) и f(b) и в дальнейшем используется вместо того из них, с которым оно совпадает по знаку. Если значение f(x) недостаточно близко к нулю, то вся процедура повторяется до тех пор, пока не будет достигнута необходимая степень сходимости e. На рис.18.4 процесс решения показан графически.
Рис.18.4. Процесс решения уравнения методом хорд Пример 3. Приведём фрагменты текста программы, которая решает задачу из примера 1 методом хорд. Program Horda; Uses Crt; Var a,b,t,x,eps:real;
Function f(x:real):real; begin {Здесь приводим выражение для вычисления функции } f:=x*x*x+x*x+x+1; end;
Begin ClrScr; Writeln(' Решение уравнения методом хорд'); { Ввод исходных данных } a:=-2; b:=1; eps:=0.001; { Начинаем расчет } Repeat x:=a-f(a)*(b-a)/(f(b)-f(a)); if f(a)*f(x)<=0 then b:=x else a:=x; Until abs(f(x))<=eps; Writeln(' Уравнение имеет корень x = ', x:10:8); Readln; End. Задания 1. Набрать текст программы Popolam. Провести вычисления и вы вывести на принтер (экран) результаты расчётов при e = 0,1; 0,01; 0,0001; 0,00001. Сравнить результат и количество итераций. 2. Сохранить под другим именем и модифицировать программу, чтобы она решала уравнение методом касательных. Сравнить результат и количество итераций при e = 0,1; 0,01; 0,001; 0,0001. 3. Сохранить под другим именем и модифицировать программу, чтобы она решала уравнение методом хорд. Сравнить результат и количество итераций при e = 0,1; 0,01; 0,001; 0,0001. 4. Сохранить под другим именем и используя три предыдущих примера, модифицировать программу, чтобы последовательно методом половинного деления, хорд и касательных уточнить корень уравнения (см. табл.), расположенный на интервале [a,b], с абсолютной погрешностью e. Определить также число итераций, необходимое для нахождения корня. Сравнить результат при e = 0,1; 0,01; 0,001; 0,0001; 0,00001. Результаты должны выводиться в виде таблицы Результаты решения уравнения методами
Варианты задания
Тема 19 Численные методы решения обыкновенных дифференциальных уравнений Дифференциальными называются уравнения, содержащие одну или несколько производных. Поскольку большая часть законов физики формулируется именно в виде дифференциальных уравнений, то инженеру приходится сталкиваться с ними. Лишь немногие из них удаётся решить без помощи вычислительных машин. Поэтому численные методы решения дифференциальных уравнений играют важную роль в практике инженерных расчётов. Чтобы решить обыкновенное дифференциальное уравнение, необходимо знать значения зависимой переменной и (или) её производных при некоторых значениях независимой переменной. Если дополнительные условия задаются при одном значении независимой переменной, то такая задача называется задачей с начальными условиями, или задачей Коши. Если же условия задаются при двух или более значениях независимой переменной, то такая задача называется краевой. В задаче Коши дополнительные условия называются начальными, а в краевой задача – граничными. Рассмотрим способы решения задачи Коши, которая формулируется следующим образом. Пусть дано дифференциальное уравнение
Требуется найти функцию y(x), удовлетворяющую как указанному уравнению, так и начальному условию. Искомая функция выражается в табличном виде
Значения x вычисляются, через малое приращение h, h=x0-x1=x2-x1. Обычно численное решение этой задачи получают, вычисляя сначала значение производной, а затем, задавая малое приращение для x, переходят к новой точке x1=x0+h. Положение новой точки определяется по наклону кривой, вычисленному с помощью дифференциального уравнения. Таким образом, график численного решения представляет собой последовательность коротких прямолинейных отрезков, которыми аппроксимируется истинная кривая y=f(x), рис.19.1. Сам численный метод определяет порядок действий при переходе от данной точки кривой к следующей.
Рис.19.1. Графическое представление численного решения задачи Коши: Наиболее простыми и известными из методов решения задачи Коши являются методы Эйлера и Рунге-Кутта. Они используются для решения дифференциальных уравнений первого порядка вида y¢=f(x,y), где y¢=dy/dx, при начальном условии y(x0)=y0. Метод Эйлера Это простейший метод решения задачи Коши, позволяющий решить дифференциальное уравнение первого порядка. Его точность невелика, поэтому на практике им пользуются редко. Однако, на основе этого метода легче понять алгоритм других, более эффективных методов. Метод Эйлера основан на разложении функции y в ряд Тейлора в окрестности x0:
Если h мало, то члены, содержащие производные второго и более высоких порядков, можно отбросить. Тогда
Рис.19.2. Принцип метода Эйлера yi+1=yi + h×f(xi,yi), i=1,2,… Графически метод Эйлера показан на рис.19.2. Ошибка метода имеет порядок h2. Пример 1. Составим программу для решения дифференциального уравнения y¢=2x2+2y при начальном условии y(0)=1; 0£ x£1 и h=0,1. Program Euler; Uses Crt; Var xn,xk,yn,h,x,y:real; i:integer;
Function f(x,y:real):real; begin {Здесь приводим выражение для вычисления функции f(x,y) } f:=2*x*x+2*y; end;
Begin ClrScr; Writeln(' Решение дифференциального уравнения '); Writeln(' dy/dx=2x^2+2y методом Эйлера '); { Ввод исходных данных } xn:=0; yn:=1; xk:=1; h:=0.1; { Выводим шапку таблицы и первую точку } Writeln('--------------------'); Writeln('| № | x | y |'); Writeln('--------------------'); { Начинаем расчет } x:=xn; y:=yn; i:=1; Writeln('|', i:2, ' |', x:5:2, ' |', y:7:4, ' |'); repeat y:=y+h*f(x,y); Writeln('|', i:2, ' |', x:5:2, ' |', y:7:4, ' |'); x:=x+h; i:=i+1; until x>xk; Writeln('--------------------'); Readln; End.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 679; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.202.168 (0.015 с.) |



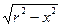 , где -r £ x £ r;
, где -r £ x £ r;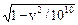 ;
; ;
; .
.





 с заданным количеством узлов интегрирования n. Аналитическое решение даёт результат 9,0. Таким образом, при условии правильного составления программы ожидаемый результат должен быть примерно равен 9. Большое число десятичных знаков при выводе результата позволяет оценить точность метода.
с заданным количеством узлов интегрирования n. Аналитическое решение даёт результат 9,0. Таким образом, при условии правильного составления программы ожидаемый результат должен быть примерно равен 9. Большое число десятичных знаков при выводе результата позволяет оценить точность метода.





 , или
, или .
.






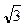

 .
.



 .
.
 =0
=0
 и начальное условие y(x0)=y0.
и начальное условие y(x0)=y0.

 .
. 



