
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача №4 (Логические функции, блок 2)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассчитать таблицу значений составной функции в соответствии с вариантом (таблица 12), вычислить сумму ее значений на заданном интервале с заданным шагом и построить график (точечную диаграмму) функции. Значения интервала изменения аргумента X выбираются в нижнем блоке Табл. 10. Пример оформления см. в приложении 1. Табл. 10. Варианты индивидуального задания №4
Задание 2 Задача №1 (решение системы линейных уравнений) На отдельном листе найти решение системы линейных уравнений методом «Обратной матрицы», выполнив задание, состоящее из следующих пунктов: · Записать систему линейных уравнений в «классическом» виде. · Ввести матрицу коэффициентов при неизвестных и правые части. · Решить систему линейных уравнений методом «Обратной матрицы». Варианты индивидуальных заданий в виде матрицы коэффициентов при неизвестных и правых частей, приведены в Табл. 11. Пятый, выделенный заливкой столбец каждого варианта — правые части уравнений. Пример оформления см. в приложении 1. Табл. 11. Варианты индивидуального задания № 5
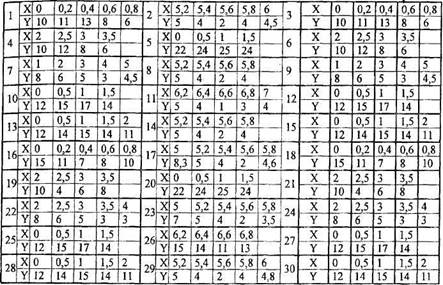
Задача № 2 (аппроксимация) На отдельном листе выполнить задание: найти аналитическую формулу зависимости Yj от X; в виде параболы Yp=a*X2+b*X+c методом наименьших квадратов. · Заполнить таблицу, включающую в себя графы: X, Y, Yp, взяв X; и X* из задания и рассчитав Yp для каждого X; по полученной формуле. · Создать диаграмму точечного типа, содержащую график «Экспериментальные точки» с зависимостью Y от X в виде точек и графиков и «Расчётные значения» с зависимостью Yp от X в виде линий без маркеров. Варианты индивидуальных заданий в виде таблицы зависимости Y; от X, содержатся в. Табл. 13. Пример оформления задачи см. в приложении 1. Описание постановки и способа решения в разделе 2.3.2. Задача аппроксимации. Табл. 12. Варианты индивидуального задания № б
Задача №3 (решение нелинейного уравнения) Найти один из корней нелинейного уравнения. Выполнение индивидуального задания должно состоять из следующих пунктов: · Отделение корня графическим методом - необходимо построить график функции, приведённой в задании, и найти хотя бы один отрезок, где он пересекает ось X, это будет приблизительное значение корня. Если ни одного отрезка найти не удалось, нужно изменить область построения. · Уточнение корня - используя два специальных средства: «Подбор параметра» и «Поиск решения», сузить найденный отрезок до 0,001. Это и будет значение корня с точностью до 0,001. Варианты индивидуальных заданий даны в Табл. 13. Табл. 13. Варианты индивидуального задания №7
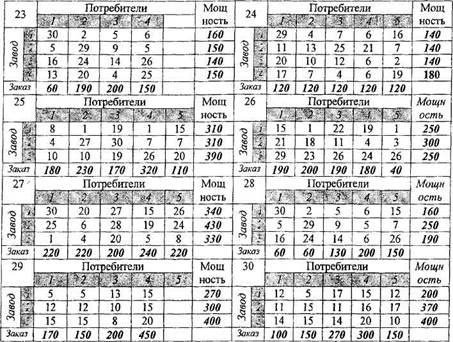
Задача№4 (транспортная задача) Выполнить задание: · Определить план перевозок, имеющий минимальную стоимость: · Создать диаграмму, иллюстрирующую оптимальный план перевозок. Варианты индивидуальных заданий приведены в Табл. 14. Образцом для оформления задания может служить пример, данный в приложении 1. Постановка задачи и методы решения описаны в разделе 2.4.2 Транспортная задача). Табл. 14. Исходные данные для решения транспортной задачи
Окончание таблицы 16.
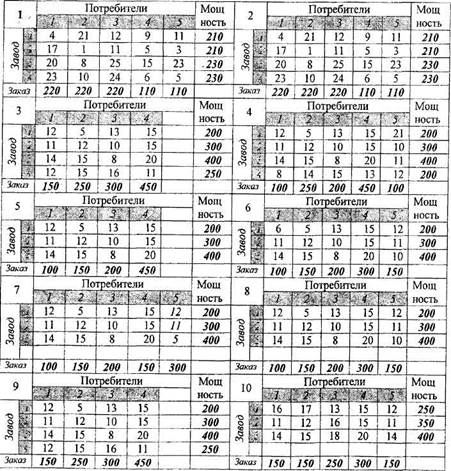
Рекомендуемый библиографический список 1. Хселир Р., Фаненштих К. Текстовый процессор Word 6.0 для Windows.- M.: Эком., 1996 2. Лукин С.Н. Word и Windows. Самоучитель для начинающих. Практические советы. М.: «Диалог-МИФИ», 2003.-273 с. 3. MS Word 97 (2000). Шаг за шагом., М.: Ecom 1999 (2000). 4. MS Excel 97 (2000). Шаг за шагом, М.: Ecom 1999 (2000). 5. Николь Н., Альбрект Р. Электронные таблицы EXCEL 5.0. М.: Эком., 1995
Пример оформления контрольной работы. Приложение 1 Задание 2 Задача №1. Построение графиков функций Задание: Ø Рассчитать таблицу значений функций
при значениях X, изменяющихся от -2 до 2 с шагом 0,1. Ø Отформатировать таблицу, используя различные варианты выравнивания текста в заголовке, форматы чисел и виды рамок Ø Создать диаграмму, содержащую графики всех трех функций. Ø Отредактировать диаграмму так, чтобы первый график был изображен линей, второй маркерами, третий- линей с маркерами. Решение.
Фрагмент таблицы в режиме отображения формул
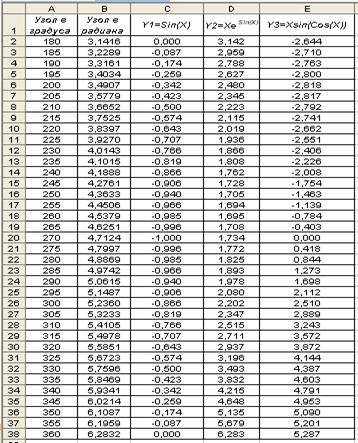
Задача №2. Построение графиков функций. Задание: Ø Рассчитать таблицу значений функций: Ø Отформатировать таблицу. Ø Создать диаграмму точечного типа на отдельном листе, содержащую первый график из приведенных в задании функций. Остальные графики добавить в процессе редактирования диаграммы. На диаграмме должно быть: её название, название осей, легенды. Ось X должна называться «Угол в градусах» и содержать значение угла в градусах. Ø Отредактировать диаграмму так, чтобы первый график был изображен линей, второй – маркерами, а третий – линей с маркерами. Решение. Значения X из градусов в радианы преобразовываем с использованием функции «РАДИАНЫ» и помещаем в дополнительный столбец и используем полученные значения в в качестве аргумента для вычисления заданных функций. Таблица значений:
Фрагмент таблицы в режиме отображения формул:
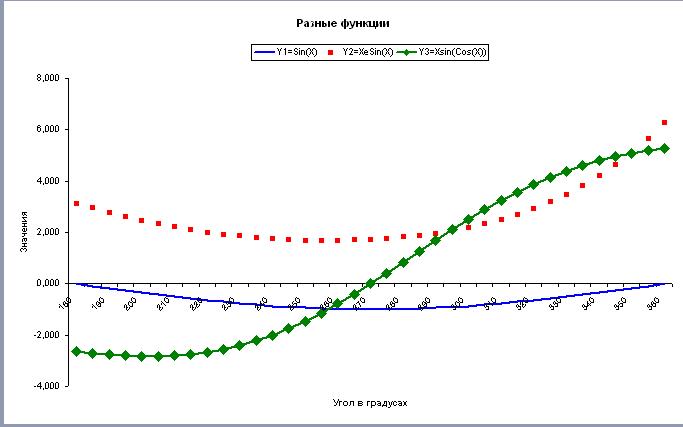
Графики функций:
Задача №3. Логические функции. Задание: Создать таблицу «Стоимость лечения» и построить круговую диаграмму распределения стоимости лечения по пациентам. Стоимость лечения = 600+ длительность_пребывания*оплата_за_день. Оплата_за_день равна 500руб. при длительности лечения менее 10 дней и 400 руб. при длительном пребывании в больнице. Решение.
Фрагмент таблицы в режиме отображения формул:
Задача №4. Логические функции (блок 2 Задание: Рассчитать таблицу значений составной функции, вычислить сумму её значений на заданном интервале с заданным шагом и построить график (точечную диаграмму) функции.
Значения изменения аргумента X: Решение.
Формула для вычисления значений составной функции: =ЕСЛИ(A2>1;COS(A2);ЕСЛИ(A2<=0;5*A2-7;A2^0,5)) Сумма вычислялась автосуммированием, значение суммы отформатировано влево.
Задание 3 Задача №1. Система линейных уравнений. Задание: Найти решение системы линейных уравнений методом обратной матрицы. Ø Записать систему линейных уравнений в «классическом виде» Ø Ввести матрицу коэффициентов при неизвестных и правые части. Ø Решить систему линейных уравнений методом «,обратной матрицы». Решение. Дана система линейных уравнений:
Ø Записать матрицу коэффициентов системы уравнений (размерность 4×4), и матрицу правых частей (размерность 4×1). Отсутствующие коэффициенты при неизвестных равны нулю. Ø При помощи функции МОБР(A2:D5) вычислить матрицу, обратную матрице коэффициентов уравнений[1]. Ø При помощи функции МУМНОЖ выполняется умножение обратной матрицы на матрицу правых частей системы уравнений. Результат операции – матрица размерностью 4×1 является решением системы линейных уравнений. Решение системы уравнений:
Задача №2. Аппроксимация. Вариант 3: Найти аналитическую формулу зависимости Yi и X, в виде параболы
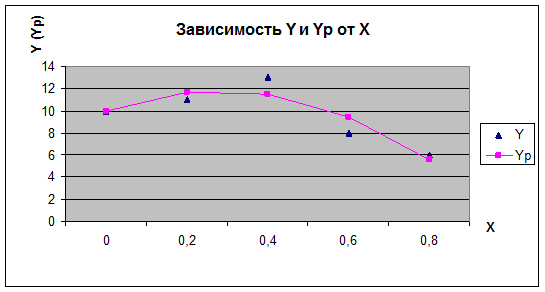
Решение. Порядок действий: Ø Формируем таблицу для вычисления коэффициентов и правых частей системы уравнений. Ø Решаем систему уравнений методом обратной матрицы. Ø Рассчитываем таблицу значений аппроксимированной функции для построения графика. На график помещаем исходный набор точек (Y) и сплошную линию, рассчитанную по формуле полученного полинома (Yр).
Набор заданных точек приближенно описывается функцией:
Задача №3. Решение нелинейного уравнения. Задание: Найти один из корней нелинейного уравнения:
Порядок действий: Ø Отделить корни графическим методом, для этого построить график функции Ø Для уточнения значения корня использованы средства «Подбор параметра» и «Поиск решения». В обоих случаях в качестве начального значения X выбираем левую границу отрезка, на котором есть корень. Решение.
Как видно из таблицы и графика функции имеет корень, на отрезке [-3;-2]. Для уточнения корня используем средства «Подбор параметра» и «Поиск решения». В обоих случаях значения корня X=-2,383. Настройка окон «Подбор параметра» и «Поиск решения».
Задача №4. Транспортная задача Задание: Имеется 5 заводов – поставщиков, производящих некоторые изделия и 5 потребителей (строек), использующих эти изделия. Мощности поставщиков, потребности строек и стоимость доставки одного изделия от любого поставщика к любому потребителю даны. Ø Определить план перевозок, имеющий минимальную стоимость. Ø Создать диаграмму, иллюстрирующую оптимальный план перевозок. Решение.
Оптимальный план перевозок содержит 9 элементов, отличных от нуля и содержится в ячейках C3:G7. для удобства отображения плана перевозок в этой области применено условное форматирование: значения, равные нулю отображаются белым цветом на белом фоне. Средства, используемые для решения задачи. Настройка окна «Поиск решения».
Расчетные таблицы в режиме отображения формул.
Диаграмма, иллюстрирующая оптимальный план перевозок.
[1] Для выполнения операции с массивами после ввода формулы нажать F2, а затем одновременно нажать на три клавиши: «Ctrl»+ «Shift»+ «Enter».
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1005; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |













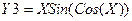




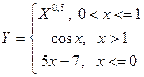








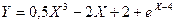 и найти хотя бы одно пересечение графика с осью X. Отрезок, на котором график функции пересекает ось X, является базовым для дальнейшего уточнения корня.
и найти хотя бы одно пересечение графика с осью X. Отрезок, на котором график функции пересекает ось X, является базовым для дальнейшего уточнения корня.









