
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание функций первой группы.Содержание книги
Поиск на нашем сайте
СУММ(число1;число2;...). Число1, число2,.. - это от 1 до 30 аргументов, для которых требуется определить итог или сумму. В качестве аргумента могут использоваться: числа, логические значения и текстовые представления чисел, непосредственно введенные в список аргументов, массивы, ссылки на одну или блок ячеек. В последнем случае суммируются только числа, а пустые ячейки, логические значения, тексты и значения ошибок в массиве или ссылке игнорируются. Причём, аргументы, которые являются значениями ошибки или текстами, непреобразуемыми в числа, вызывают ошибки. Например: СУММ(3; 2) равняется 5,а СУММ("3"; 2; ИСТИНА) равняется 6, так как текстовые значения преобразуются в числа, а логическое значение ИСТИНА преобразуется в число 1. Если ячейки А2:Е2 содержат числа 5, 15, 30, 40 и 50, то СУММ(А2:С2) равняется 50, а СУММ(В2:Е2; 15) равняется 150
Рис. 9.Фрагмент электронной таблицы СУММПРОИЗВ(массив1;массив2;массивЗ;...). Массив1, массив2, массивЗ,... - это от 2 до 30 массивов, чьи компоненты нужно перемножить, а затем сложить. Массивы, используемые в качестве аргументов, должны иметь одинаковые размерности. Если это не так, то функция СУММПРОИЗВ возвращает ошибку #ЗНАЧ!. СУММПРОИЗВ, трактует нечисловые элементы массивов как нулевые. Например, перемножить компоненты двух массивов, приведённых на, можно, используя следующие варианты: СУММПРОИЗВ({3;4:8;6:1;9}; {2; 7:6; 7:5; 3}) или СУММПРОИЗВ(А 1:B3;D1:E3). В обоих случаях вычисления производятся по формуле: 3*2 + 4*7 + 8*6 + 6*7 + 1*5 + 9*3, а результат равняется 156 МИН (число 1;число2;...)или МАКС(число1;число2;...). Число!, число2,... - это от 1 до 30 аргументов, среди которых ищется минимальное или максимальное значение. Можно задавать аргументы, которые являются числами, пустыми ячейками, логическими значениями или текстовыми представлениями чисел. Аргументы, которые являются значениями ошибки или текстами, не преобразуемыми в числа, вызывают появление ошибок. Если аргумент является массивом или ссылкой, то в нем учитываются только числа. Пустые ячейки, логические значения или текст в массиве или ссылке игнорируются. Если аргументы не содержат чисел, то функция возвращает 0 (ноль). Например, если используются данные, приведённые на рис.19, то МАКС(А1:ВЗ) равняется 9, МАКС(А1:ВЗ;30) равняется 30, а Мин(А1:B3;D1:ЕЗ) равняется 1.
Описание функций второй группы. МОБР(массив). Возвращает обратную матрицу для матрицы, хранящейся в массиве. Массив - это числовой массив с равным количеством строк и столбцов. Массив может быть задан: как диапазон ячеек, например, А1:СЗ; как массив констант, например, {1;2;3: 4;5;6: 7;8;9} или как имя диапазона или массива. При использовании массива констант для разделения чисел в строке используется «;» а для разделения строк «:». Если какая-либо из ячеек в массиве пуста или содержит текст, а также если массив имеет неравное число строк и столбцов, то функция МОБР возвращает ошибку #ЗНАЧ!. МУМН0Ж(массив1;массив2). Возвращает произведение матриц (матрицы хранятся в массивах). Результатом является массив с таким же числом строк, как массив 1, и с таким же числом столбцов, как массив2. Массив1, массив2 - это перемножаемые массивы. Количество столбцов аргумента массив 1 должно быть таким же, как количество сток аргумента массив2, и оба массива должны содержать только числа. Массив! и массив2 могут быть заданы как интервалы, массивы констант или ссылки. Если хотя бы одна ячейка в аргументах пуста или содержит текст, или если число столбцов в аргументе массив 1 отличается от числа строк в аргументе массив2, то функция МУМНОЖ возвращает ошибку #ЗНАЧ!. Решение системы линейных уравнений. Решаем систему линейных уравнений методом обратной матрицы. Для этого необходимо: > Разместить на рабочем листе матрицу коэффициентов при > Вычислить обратную матрицу при помощи функции МОБР; > Вычислить значения неизвестных, умножив обратную матрицу Задача аппроксимации. Постановка задачи: Дана дискретная (табличная) зависимость Y1 от Xi. Требуется найти ее аналитическую формулу (аппроксимирующую зависимость) в виде параболы Yp = а*Х2 + Ь*Х + с. Таким образом, задача сводится к нахождению числовых значений коэффициентов а, Ь, и с. При использовании метода наименьших квадратов эти значения находятся как решение системы трех линейных уравнений (1) с тремя неизвестными а, Ь, с. Для этого выполнить следующие действия: ·
· Записать матрицы коэффициентов и правых частей системы (1). Коэффициенты при неизвестных а, b, с и правые части - это суммы из последней строки расчетной таблицы, а коэффициент «п» равен количеству точек в исходной таблице. · Решить систему линейных уравнений методом «Обратной матрицы как описано в разделе 2.3.1. · Выписать искомое выражение для Ур и рассчитать значения полученной функции для исходных значений Xi. · Проверьте себя: значения Yp и Yi в соответствующих точках должны быть достаточно близки.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 223; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.57.152 (0.006 с.) |


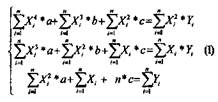 На рабочем листе создать таблицу для расчета коэффициентов и правых частей системы линейных уравнений (1). В каждом столбце таблицы вычисляется один из коэффициентов или правых частей системы (1). При этом Xj и Yi-значения, данные в исходной таблице. В последней строке таблицы вычислить суммы по столбцам.
На рабочем листе создать таблицу для расчета коэффициентов и правых частей системы линейных уравнений (1). В каждом столбце таблицы вычисляется один из коэффициентов или правых частей системы (1). При этом Xj и Yi-значения, данные в исходной таблице. В последней строке таблицы вычислить суммы по столбцам.


