
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Что называется дифференциалом функции? Чему он равен?Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Каков геометрический смысл дифференциала функции? 3. Свойства дифференциала. Формулы для приближенных подсчетов. Как найти погрешности приближенного приращения функции? Практическая работа №5 «Полное исследование функции. Построение графиков» Цель: сформировать навыки исследования функции по общей схеме и построения ее графика.
Теоретическая часть С помощью производной решаются самые разнообразные прикладные задачи. В частности понятие производной является мощным инструментов для исследования функции. Функция если Из данного определения вытекает, что для возрастающей функции приращения аргумента и функции имеет один и тот же знак, в силу чего их отношение положительно: Теорема. Если функция f имеет положительную производную в каждой точке интервала l,то эта функция возрастает на этом интервале. Если функция f имеет отрицательную производную в каждой точке интервала l, то эта функция убывает на этом интервале.
Точки, в которых производная функции равна нулю, называются стационарными точками функции. Точки, в которых производная функции равна нулю или не существует, называются критическими точками. Те значения аргумента, при которых функция достигает своих наибольших и наименьших по сравнению с близкими значений, называются точками максимума и минимума Определение. Tочка х0 называется точкой минимума функции f, если найдётся такая окрестность точки х0, что для всех х из этой окрестности f(x0)
Определение. Tочка х0 называется точкой максимума функции f, если найдётся такая окрестность точки х0, что для всех х из этой окрестности f(x0)
Точки минимума и максимума называются точками экстремумов данной функции, а значения функции в этих точках называются экстремумами функции. Теорема (Ферма). Если х0 является точкой экстремума функции f и в этой точке существует производная, она равна нулю: f '(x0)=0. Обращение первой производной в нуль является необходимым, но не достаточным условием экстремума. Теорема (Первое достаточное условие существования экстремума). Пусть функция f(x) дифференцируема в некоторой окрестности точки х0. Если при переходе через точку х0 слева направо производная f /(x)меняет знак с плюса на минус, то в точке х0 функция f(x) имеет максимум. Если же при переходе через точку х0 производная f /(x)меняет знак с минуса на плюс, то в точка х0 является точкой минимума
f (х 0) f (х 0)
Более полным будет исследована функция, если найдем промежутки выпуклости функции с помощью второй производной. Если для любых точек x1 и x2 отрезка [a; b] секущая AB проходит под графиком функции f (x), то функция f выпукла вверх. Аналогично определяется функция, выпуклая вниз. Дважды дифференцируемая на [a; b] функция f (x) выпукла вверх, если для любого Дважды дифференцируемая на [a; b] функция f (x) выпукла вниз, если для любого
Так, вторая производная функции точка х0 называется точкой перегиба функции f, если в этой точке изменяется направление ее выпуклости. Необходимое условие наличия точки перегиба. Если х0 – точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то
Часто встречаются задачи, где нужно найти наибольшее и наименьшее значение функции на отрезке. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b]. Общая схема построения графиков функций: 1) Найти область определения функции. 2) Исследовать функцию на четность или нечетность, периодичность. 3) Найти точки пересечения графика функции с осями координат. 4) Найти точки разрыва, асимптоты графика функции. 5) Исследовать функцию с помощью первой производной (Найти интервалы монотонности и экстремумы функции). 6) Исследовать функцию с помощью второй производной (Найти интервалы выпуклости и точки перегиба). 7) Найти дополнительные точки, если это необходимо. 8) Построить график, используя полученные результаты исследования.
Практическая часть
Пример 1. Построить график функции y=x3-6x2+9x-3. 1) D(x)=R. 2) y(-x)=(-x)3-6(-x)2+9(-x)-3=-x3-6x2-9x-3, функция не является ни четной, ни нечетной. Функция непериодическая. 3) Т. пересечения с осью Оу; х=0, у=-3. (0;-3) 4) Функция не имеет точек разрыва, следовательно, вертикальных асимптот нет. Т.к 5) Найдем производную данной функции: y′=3x2-12x+9. Решим уравнение y′=0: 3х2-12х+9=0, х2-4х+3=0, х1=1, х2=3.
Исследуемая функция в промежутках х<1 и x>3 возрастает, а на промежутке 1<x<3 убывает; х=1 – точка максимума, х=3 – точка минимума. ymax=y(1)=1, ymin=y(3)=-3. Удобно представить результаты исследования в таблицу:
6) Найдем вторую производную: у′′=6x-12; y′′=0 при х=2. Точка х=2 делит область определения функции на два промежутка: х<2 и x>2.
В первом из них у′′<0, а во втором y′′>0, т.е. при х<2 кривая выпукла вверх, а при x>2 выпукла вниз; х=2 – точка перегиба; у(2)= -1. 7)
Пример 2. Провести полное исследование функции Решение:
1. Областью определения функции является множество 2. Так как 3. Найдем точки пересечения графика функции с осями координат. а) С осью б) С осью 4. Функция претерпевает разрыв в точках x=-1, x=1. х=-1 и x=1—вертикальные асимптоты.
У=-1—горизонтальная асимптота. у=0—горизонтальная асимптота. 5. Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции.
Из уравнения
Внесем полученные результаты в таблицу:
6. Исследуем график функции на выпуклость, вогнутость и определим точки перегиба. Для этого найдем вторую производную функции
Уравнение
Несмотря на то, что при переходе через точки х=-1 и х=1 вторая производная меняет знак, они не являются точками перегиба, так как они не входят в область определения функции. Таким образом, точек перегиба у графика функции нет.
Практические задания
Построить графики функции: 1) y=x ln x. 8) 2) y=(x-1)ex. 9) 3) 4) 5) 6) 7) Контрольные вопросы: 1. Какая функция называется возрастающей? Убывающей? 2. Сформулируйте условия возрастания и убывания функции. 3. Что называется стационарной точкой? Критической точкой первого? 4. Сформулируйте первое достаточное условие существования экстремума. 5. Сформулируйте теорему Ферма. 6. Сформулируйте необходимое условие наличия точки перегиба 7. Алгоритм исследования и построения графика функции.
Практическая работа №6 «Неопределенный интгерал»
Цель работы: Сформировать навыки нахождения неопределенного интеграла методом непосредственного интегрирования, замены переменной, интегрирования по частям. Теоретическая часть. Пусть функция у=F(х) (1) имеет производную f(x), тогда ее дифференциал dy=f(x)dx. Функция (1) по отношению к ее дифференциалу называется первообразной. Определение 1. Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство: F¢(x) = f(x). Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число. F1(x) = F2(x) + C. Определение 2. Совокупность всех первообразных для функции f(x), определенных на некотором промежутке X, называется неопределенным интегралов от функции f(x) на этом промежутке и обозначается символом ∫ f(x)dx.
где С – некоторая постоянная. Определение 3. Геометрически неопределенный интеграл представляет собой семейство интегральных кривых, каждая из которых получается из любой другой кривой параллельным переносом вдоль оси Oy.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 560; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.008 с.) |

 , определенная во всех точках промежутка
, определенная во всех точках промежутка  , называется возрастающей (убывающей) в этом промежутке, если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует большее (меньшее) значение функции, т. е,
, называется возрастающей (убывающей) в этом промежутке, если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует большее (меньшее) значение функции, т. е,

 , то при
, то при  – возрастающая,
– возрастающая,  – убывающая.
– убывающая. . Для убывающей функции эти приращения имеют разные знаки, в силу чего
. Для убывающей функции эти приращения имеют разные знаки, в силу чего  .
.

 f(x).
f(x). f(x).
f(x).
 у max у
у max у
 .
.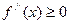
 равна
равна  ,откуда следует, что квадратичная функция выпукла вниз на всей области определения.
,откуда следует, что квадратичная функция выпукла вниз на всей области определения.
 нет и наклонных асимптот.
нет и наклонных асимптот.
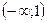
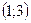






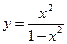 .
. .
. функция является четной, непериодическая.
функция является четной, непериодическая. :
:  , у=0, т.е. точка пересечения с осью
, у=0, т.е. точка пересечения с осью  .
. :
:  ,
, 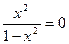 , х=0, т.е. точка пересечения с осью
, х=0, т.е. точка пересечения с осью  .
.


 получаем
получаем  откуда х=0.
откуда х=0.







 не имеет корней.
не имеет корней.



 10)
10) 
 11)
11) 
 12)
12) 
 13)
13) 
 14)
14) 
 ,
,


