Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление площадей плоских фигур с помощью определенного интеграла ⇐ ПредыдущаяСтр 5 из 5
Рассмотрим несколько случаев применения определенного интеграла для нахождения площадей плоских фигур. 1. Пусть на отрезке [a;b] дана непрерывная неотрицательная функция y=f(x).
Т.е. 2. Фигура ограничена графиком непрерывной неположительной функции, прямыми х=а, х=b и осью Ох. Тогда
3. Фигура ограничена графиками двух непрерывных на отрезке функциями y=f(x) и y=g(x) и прямыми х=а, х=b, где
4. Фигура прилегает к оси ординат и ограничена непрерывной кривой x=f(y), прямыми х=а, х=b и осью Оу. Тогда
Объем тел вращения.
Т.к. каждое сечение тела плоскостью x = const представляет собой круг радиуса
Если же необходимо найти объем тела, полученного вращением графика непрерывной на отрезке [a, b] функции у=f(x) вокруг оси Оу, то применяем формулу Y
d y=f(x) c Х
Вычисление пути, пройденного точкой Если точка движется прямолинейно и ее скорость v=f(t) есть известная функция временны t, то путь пройденный точкой за промежуток времени
Работа переменной силы Если переменная сила F=F(x) действует в направлении оси Ох, то работа силы на отрезке
Практическая часть Пример 1. вычислить площадь тела ограниченной области, лежащей между графиками Решение. Построим графики данных функции по точкам. Эти графики имеют две общих точек. х1 =0, х2=1. При этом график функции Значит, по формуле (3) площадь области
Пример 2. Вычислить объем тела, полученного от вращения графика функции
Решение. Используем формулу (5)
Пример 3. Скорость движения точки изменяется по закону
Решение. По условию f(x)=(t2+4t-2), t1=0, t2=6. По формуле (7) имеем:
Пример 4. Вычислите работу, произведенную при сжатии пружины на 0,03 м, если для сжатия ее на 0,02 м нужна сила 10 Н. Решение. Согласно закону Гука F=kx. Т.к. х=0,02 при F=10Н, то
По формуле (8) имеем:
Практические задания
Контрольные вопросы:
1. Геометрический смысл определенного интеграла. 2. Какие прикладные задачи можно решать с помощью определенного интеграла? 3. Запишите формулу для вычисления пройденного пути. 4. Запишите формулу для нахождения работы силы. 5. Запишите формулу для нахождения объема тел вращения. 6. Какие еще знаете примеры применения на практике определенного интеграла? Практическая работа №9 «Решение дифференциальных уравнений первого порядка» Цель: сформировать навыки решения дифференциальных уравнений с разделяющимися переменными, однородных дифференциальных уравнений первого порядка, линейных уравнений первого порядка.
Теоретическая часть Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту или иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков. Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции. Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения. Определение. Общим решением дифференциального уравнения называется такая дифференцируемая функция y=f(x,C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество. С геометрической точки зрения решением дифференциальных уравнений является семейство интегральных кривых. При решении конкретных задач часто необходимо выделить из всей совокупности решений дифференциального уравнения то частное решение, которое удовлетворяет заданным начальным условиям. Задача Коши Найти решение у=у(х) уравнения у′=f(x, y), удовлетворяющее при заданных начальных данных (х0, у0) начальному условию у(х0)=у0, называется задачей Коши. 1. Дифференциальные уравнения с разделяющимися переменными Дифференциальное уравнение называется уравнением с разделяющимися переменными, если имеет следующий вид: y′=f1(x)∙f2(y) (1) Предположим, что
Уравнение (2) называется уравнением с разделенными переменными. Интегрируя почленно уравнение (2), получим общее решение уравнения (1)
Алгоритм решения 1) Разделить переменные (с учетом условий, когда это можно сделать). 2) Интегрировать почленно полученное уравнение. 3) Выяснить, имеет ли уравнение решение, не получившего из общего интеграла. 4) Найти частное решение (если нужно).
2. Однородные ДУ первого порядка Определение. Функция f(x, y) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:
Например, функция
Определение. Уравнение вида P(x, y)dx+Q(x, y)dy=0, (3) где P(x, y), Q(x, y) – однородные функции x и y одинаковой степени, называется однородным дифференциальным уравнением. Уравнение (3) можно привести к виду Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными с помощью подстановки
После решения полученного ДУ относительно u, нужно выразить u через x и у и решить новое ДУ с разделяющимися переменными.
3. Линейные ДУ первого порядка Определение. Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:
при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением. Рассмотрим методы нахождения общего решения линейного однородного дифференциального уравнения первого порядка вида
Такого типа дифференциальные уравнения можно свести к уравнениям с разделенными переменными.
Для интегрирования линейных неоднородных уравнений (Q(x)¹0) применяется основном метод Бернулли. Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций y=uv, где u=u(x), v=v(x)—некоторые функции от x, тогда y/=u/v+uv/. Этот метод более подробно рассмотрен в практической части.
Практическая часть Пример 1. Решить дифференциальное уравнение: y′tgx=1+y, если Решение. Уравнение является дифференциальным уравнением с разделяющимися переменными, где f1(x)=tgx, f2(y)=1+y.
ln|1+y|=ln|sinx|+C1 , 1+y=sin x y=Csin x-1. Находим С, подставляя в данное равенство начальные данные условия.
Таким образом, y=sin x-1. Ответ: y=sin x-1. Пример 2. Решить уравнение Решение. Заданное уравнение имеет вид (3), т.е. является однородным диф. уравнением первого порядка. Приведем его к виду (4):
Пусть
Ответ:
Пример 3. Решить уравнение (x2-2y2)+2xy Решение. (x2-2y2)+2xy (x2-2y2)dx+2xydy=0. В данном уравнении функции P(x, y)=x2-2y2, Q(x, y)=2xy – однородные второго измерения, следовательно, данное уравнение является однородным дифференциальным уравнением первого порядка. Положим, у=ux, откуда: dy= udx+x du. Уравнение примет вид: x2dx-2(zx)2dx+2x ux(u dx+x du)=0, x2dx-2u2x2dx+2u2x2dx+2ux3du=0, dx+2uxdu=0,
Учитывая, что u=y/x, находим общий интеграл
Ответ: Пример 4. Найти общее решение уравнения Решение. Данное уравнение имеет вид (4), т.е. является линейным уравнением. Пусть y=uv, y/=u/v+uv/.Тогда уравнение примет вид:
Подберем функцию так, чтобы выражение в скобках было равно нулю, т.е.
Интегрируя равенство, получим
Подставим полученное решение в (6).
Итак, общее решение Ответ:
Практические задания
1-2-- Найти общее решение ДУ с разделяющимися переменными. 3-- Найти частное решение ДУ с разделяющимися переменными. 4--Найти общее решение однородного ДУ первого порядка. 5-- Найти общее решение линейного ДУ первого порядка.
Контрольные вопросы: 1. Что называется дифференциальным уравнением? 2. Как определить порядок диф. уравнения? 3. Что называется общим решением диф. уравнения? Частным? 4. Диф. Уравнения с разделяющимися переменными. Алгоритм их решения. 5. Однородные диф. уравнения первого порядка. Алгоритм их решения. 6. Линейные диф. уравнения первого порядка. Алгоритм их решения (Метод Бернулли).
Пояснительная записка Методические рекомендации по выполнению практических задании по дисциплине «Элементы высшей математики» для студентов 2 курса специальности составлены в соответствии стандартам ГОУ СПО и рабочей программе, составленной автором и утвержденным 09.2008г. В данном пособии приведены двадцать пять практических работ. Каждая работа состоит из четырех частей: § Теоретическая часть, где даются все основные определения, теоремы, формулы, теоретические выкладки по данной теме; § Практическая часть, состоящая из решений всех стандартных задач приведенных в практических заданиях; § Практические задания в четырнадцати вариантах; § Контрольные вопросы. В пособии также включена дополнительная глава «Несобственные интегралы», экзаменационные вопросы, список литературы. Пособие можно рекомендовать студентам и для подготовки к практическим занятиям, семинарам, зачету, экзамену.
Используемая литература 1. Лисичкин В.Т., Соловейчик И.Л. Математика: Учеб. Пособие для техникумов.-М.: Высш. Шк.,1991 2. Валуцэ И.И., Дилигул Г.Д., Математика для техникумов.-М.: Наука, 1990. 3. Зайцев И.Л. Элементы высшей математики.-М.: Наука, 1972 4. Богомолов Н.В., Практические занятия по математике: Учеб. Пособие для техникумов.-М.:Высш. Шк.,1990
СОДЕРЖАНИЕ
1. Вычисление пределов функции. Классификация точек разрыва……3 2. Правила дифференцирования. Производная сложной функции..... 17 3. Раскрытие неопределенностей. Правило Лопиталя.………………..23 4. Дифференциал функции. Приближенные вычисления ………....….29 5. Полное исследование функции. Построение графиков.……………35 6. Неопределенный интеграл……….……………………………………42 7. Вычисление определенного интеграла………………………………50 8. Приложение определенного интеграла ………………………..……..56 9. Решение дифференциальных уравнений первого порядка …..…....63
|
||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 819; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.203 (0.139 с.) |
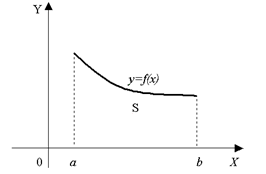
представляет собой площадь криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми х=а, х=b и осью Ох. В этом и состоит геометрический смысл определенного интеграла.
(1)
(2)
. Тогда
(3)
. (4)
Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения.
, то объем тела вращения может быть легко найден по полученной выше формуле:
(5)
(6)
, вычисляется по формуле
(7)
вычисляется по формуле
(8)
и 
.
между графиками равна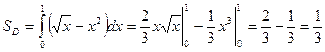
[1;3] вокруг оси Ох.
. Подставляя значение k в закон Гука, имеем: f(x)=500x.
(Дж)
б) 
.
2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями х=0, х=6, у=0,5х+4 и у=0.
3. Скорость движения точки изменяется по закону 
2. Часть синусоиды y=sinx вращается вокруг оси Ох. Найдите объём тела вращения от 
до 
3. Скорость движения точки изменяется по закону 
2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у2=6х, у=1, х=1, х=3.
3. Скорость движения точки изменяется по закону 
б) 
2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями х=0, х=3, х+у-3=0 и у=0.
3. Скорость падающего в пустоте тела изменяется по формуле 
б) 
2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у=х2-4, у=0.
3. Скорость движения точки изменяется по закону 
.
б) 
2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у=sinx, y=0, x=0, x=π.
3. Скорость движения точки изменяется по закону 
2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями х=0, х=3, у=х-3 и у=0.
3. Скорость падающего в пустоте тела изменяется по формуле 
б) 
2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями y2=4x, y=0, х=0, х=4
3. Скорость движения точки изменяется по закону
.
3. Скорость движения точки изменяется по закону 
2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями y2=8x, y=0, х=1, х=4.
3. Скорость движения точки изменяется по закону 
2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями: у=sin2x, y=0, x=0, x=π/2.
3. Скорость падающего в пустоте тела изменяется по формуле 
б) 
2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями: 
3. Скорость движения точки изменяется по закону 
б) y=x2+2x+2, y=2-4x-x2.
2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у=cosx, y=0, x=0, x=π.
3. Скорость движения точки изменяется по закону 
. Тогда уравнение можно записать так:
(2)
.
является однородной третьего порядка, т.к.
(4)
, т.е. y=ux и y/=u/x+u
(4)
(5)
,
при 
;
,
С=1.
.
и уравнение привет вид:
т.к. 
то
-- общее решение заданного уравнения.
. 
=0
,
, 
, 
(6)
,
,
,
.
.
.
.
4. 
5. y/+2xy=2xy3
.
y3dx=0, если у =1 при х =-1.
.
.
dx
, если у=4 при х=0
, если у=1 при х=1.
, если у=0 при х=1
, если у=1 при х=0.
