
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства определенного интегралаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1) Определенный интеграл с симметричными пределами равен нулю: 2) При перемене местами пределов интегрирования величина определенного интеграла меняется на противоположную величину:
3) Если отрезок интегрирования разделен на конечное число частичных отрезков, то определенный интеграл от функции f(x) на отрезке [a,b] равен сумме определенных интегралов от этой функции на каждом из частичных отрезков:
a c k b 4) Постоянный множитель можно выносить за знак определенного интеграла:
5) Интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов этих функций, т.е.
6) Если подынтегральная функция в интервале интегрирования не меняет знака, то интеграл представляет собой число того же знака, что и функция. В частности, если f(x)≥0 в интервале [a,b], где а<b, то и
7). Если одна из функций, интегрируемых на отрезке [a,b] (причем, а<b), больше другой во всех точках данного отрезка, то определенный интеграл от первой функции соответственно больше определенного интеграла второй функции, то есть, если 8). Определенный интеграл от непрерывной функции f(x) на конечном отрезке [a,b] равен произведению величины этого отрезка на значение данной функции в некоторой точке с, находящейся внутри этого отрезка:
Методы интегрирования 1) Метод непосредственного интегрирования. Пример: Пример:
2) Метод замены переменной. Пример: При замене переменной меняются и пределы интегрирования, которые следует находить из соотношения замены 1+t=k, где вместо t подставляем старые пределы интегрирования, а k дает значение новых пределов. Пример:
3) Метод интегрирования по частям: Пример: Пример:
Применение определенного интеграла.
1). Вычисление площадей плоских фигур
Пример: Вычислить площадь фигуры АВСD. Решение:
Пример: Вычислить площадь фигуры, ограниченной кривыми Решение: Найдем точки пересечения кривых, для этого приравняем у1 и у2:
Пусть дана криволинейная трапеция, ограниченная кривой у=f(x), осью ОХ и прямыми х=а и х=b. Вращая эту фигуру вокруг оси ОХ, получим тело вращения. Для вычисления объема тела вращения применяется формула:
Пример: Вычислить объем тела, образуемого вращением вокруг оси ОХ трапеции, ограниченной линиями у=х/2+4, у=0, х=0, х=6.
куб.единиц.
3) Определение поверхности тела вращения.
Si = 2πr∙ dl, но
Понятие двойного интеграла.
Понятие определенного интеграла может быть обобщено в различных направлениях. До сих пор областью интегрирования простого определенного интеграла был отрезок Рассмотрим общий вид двойного интеграла: При нахождении двойных интегралов используются те же приемы, которые были рассмотрены ранее. Пример:
Пример: Найти площадь поверхности конуса высотой H, представленного на рисунке. Решение: Площадь поверхности такого конуса можно найти как сумму элементарных площадок ds, на которые разбивается вся его поверхность. Площадь ds рассчитывается как произведение длины элементарной площадки на ее высоту. Длина площадки ds равна произведению радиуса сечения конуса (r) на элементарный угол (dφ), где радиус сечения является катетом прямоугольного треугольника и определяется через другой его катет z и противолежащий угол α по формуле:
Пример: Найти интеграл по поверхности конуса:
так как
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 830; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.75.247 (0.007 с.) |

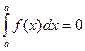
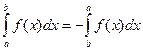


 .
.
 . Это свойство называют свойством монотонности определенного интеграла.
. Это свойство называют свойством монотонности определенного интеграла. , то
, то  .
. , где f(с) называется средним значением функции на интервале [a,b].
, где f(с) называется средним значением функции на интервале [a,b].

 │
│  , где 1 + t = k, а dt=dk.
, где 1 + t = k, а dt=dk.
 │
│  .
.





 и
и  .
. . Данное тождество верно при х=0 и х=1. Тогда площадь фигуры, ограниченной кривыми
. Данное тождество верно при х=0 и х=1. Тогда площадь фигуры, ограниченной кривыми  .
. 2) Вычисление объема тел вращения.
2) Вычисление объема тел вращения. , где S = π y² - площадь сечения, а S∙∆x= π y²Δ x - объем выделенного кусочка.
, где S = π y² - площадь сечения, а S∙∆x= π y²Δ x - объем выделенного кусочка. Решение:
Решение:
 Пусть есть конус с осью симметрии z и образующей, составляющей угол α с осью z. Разобьем поверхность конуса на небольшие участки, проведя плоскости перпендикулярно оси z. Тогда площадь выделенного участка будет равна
Пусть есть конус с осью симметрии z и образующей, составляющей угол α с осью z. Разобьем поверхность конуса на небольшие участки, проведя плоскости перпендикулярно оси z. Тогда площадь выделенного участка будет равна , а
, а 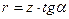 , следовательно
, следовательно .
. числовой прямой. Если за область интегрирования взять некоторую плоскую площадку, то получится двойной интеграл, если часть поверхности – то поверхностный интеграл, если отрезок некоторой кривой линии – то криволинейный интеграл.
числовой прямой. Если за область интегрирования взять некоторую плоскую площадку, то получится двойной интеграл, если часть поверхности – то поверхностный интеграл, если отрезок некоторой кривой линии – то криволинейный интеграл. .
.

 .
.
 , так как она расположена под углом α к оси z. Тогда вся поверхность конуса:
, так как она расположена под углом α к оси z. Тогда вся поверхность конуса: 
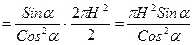 .
.

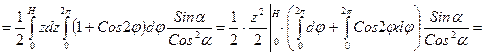
 ,
, .
.


