
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка правильности нахождения неопределенного интеграла.Содержание книги
Поиск на нашем сайте
Проверка правильности нахождения неопределенного интеграла основана на его первом свойстве, в соответствии с которым производная найденного неопределенного интеграла должна быть равна подынтегральной функции. Иными словами, для проверки результата интегрирования достаточно найти производную этого результата, и лишь в случае ее совпадения с подынтегральной функцией исходного интеграла, а также при наличии в результате интегрирования произвольной постоянной можно сделать вывод о том, что интеграл найден верно. Раздел 6. Определенный интеграл.
Понятие определенного интеграла. Понятие определенного интеграла используют в ряде практических задач, в частности в задачах по вычислению площадей плоских фигур, расчету работы, производимой переменной силой, количества вещества, образовавшегося в результате химической реакции.
Пусть задана функция y = f (t) скорость протекания химической реакции в зависимости от времени. Тогда общее количество препарата можно найти, если разделить все время наблюдения за реакцией на очень маленькие отрезки, а затем умножить среднюю скорость реакции на каждом отрезке на его длину и просуммировать по всем отрезкам, то есть получим: Полученное выражение имеет название интегральной суммы на отрезке Интегральная сумма – это сумма по всем n-отрезкам, на которые разбит рассматриваемый интервал, произведений среднего значения функции на каждом частичном интервале на длину соответствующего интервала.
Предельное значение этой суммы при стремлении к нулю частичного интервала
Определение: Определенным интегралом называется предел, к которому стремиться интегральная сумма при стремлении к нулю длины наибольшего частичного интервала.
Геометрическая и физическая интерпретация определенного интеграла.
Определение: Плоская фигура, ограниченная сверху графиком непрерывной функции y=f(x), снизу – осью абсцисс, слева – прямой линией х=а, а справа – прямой линией х=в, называется криволинейной трапецией.
Очевидно, что площадь данной криволинейной трапеции равна сумме площадей составляющих ее криволинейных трапеций и численно равна определенному интегралу от функции y=f(x) на отрезке [a,b]. Таким образом, геометрический смысл определенного интеграла - это площадь криволинейной трапеции.
1) это работа, совершенная переменной силой при перемещении тела из точки а в точку в.
2) с помощью определенного интеграла можно также найти путь, пройденный телом за промежуток времени
Формула Ньютона-Лейбница. Непосредственное вычисление интеграла как предела соответствующих интегральных сумм затруднительно, да и не требуется, поскольку для этой цели можно воспользоваться формулой Ньютона–Лейбница. Согласно которой, значение определенного интеграла равно разности значений его первообразных, взятых на верхнем и нижнем пределах интегрирования:
Несобственный интеграл.
Если этот предел существует, то несобственный интеграл называется сходящимся, а если не существует, то расходящимся.
Аналогично определяются несобственные интегралы и для прочих бесконечных интервалов (-∞,b] и (-∞,∞).
Несобственный интеграл можно интерпретировать как площадь бесконечной криволинейной трапеции.
Пример:
|
|||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1077; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.104.12 (0.01 с.) |

 То есть, если нам надо знать не зависимость протекания какого-либо процесса во времени и пространстве, а его результат (например, количество вещества, образовавшегося в результате химической реакции), то мы приходим к понятию определенного интеграла.
То есть, если нам надо знать не зависимость протекания какого-либо процесса во времени и пространстве, а его результат (например, количество вещества, образовавшегося в результате химической реакции), то мы приходим к понятию определенного интеграла. , где
, где  - средняя точка на отрезке.
- средняя точка на отрезке. .
. записывается через определенный интеграл функции f(x):
записывается через определенный интеграл функции f(x):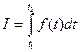 .
.
 Физический смысл определенного интеграла:
Физический смысл определенного интеграла: ;
; .
. , где F(x) – первообразная функция f(x).
, где F(x) – первообразная функция f(x).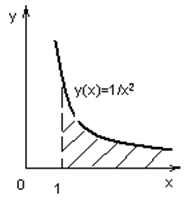 Интеграл с бесконечными пределами называется несобственным и находится как:
Интеграл с бесконечными пределами называется несобственным и находится как:




