
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра высшей математики, информатики, биостатистики, доказательной медициныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кафедра высшей математики, информатики, биостатистики, доказательной медицины Н.В. Маркина, А.А. Болотов Учебное пособие по элементам высшей математики для студентов высших медицинских учебных заведений Челябинск, 2008 г. УДК 510
Утверждено на заседании кафедры математики, информатики, биостатистики, доказательной медицины протокол № от и центральным методическим советом Чел.ГМА.
Н.В. Маркина, А.А. Болотов
Учебное пособие по элементам высшей математики для студентов высших медицинских учебных заведений.
Пособие написано в соответствии с программой по высшей математике и информатике для студентов первого курса медицинских высших учебных заведений. Объем усл. печ. л.
Тираж 500 экз.
© ИМБДМ
Введение.
Настоящее пособие по основам высшей математики предназначено, в основном, для понимания курса биофизики в медицинских учебных заведениях. В курсе биофизики рассмотрение процессов в живых системах дается на уровне количественных закономерностей (электрогенез, биореология, биофизика клетки). Как правило, биофизические закономерности представляются в виде уравнений или функций. Для описания процессов используются дифференциальные уравнения. Таким образом, основным языком изложения материала биофизики является язык высшей математики и, в первую очередь, дифференциальное и интегральное исчисления. С учетом, как правило, недостаточно высокого исходного уровня подготовки студентов по математике при изложении теоретической части материала основной упор сделан не на строгих математических доказательствах теорем и их свойств, а на их смысле и возможности практического применения. Пособие содержит большое количество примеров и задач.
Раздел 1. Число. Переменная. Функция. Действительные числа. Числовая последовательность. Величина. Область изменения величины.
С помощью чисел мы можем количественно выражать различные свойства предметов и явлений. В этом случае число будет отражать значение рассматриваемой величины (например: масса тела равна 3 кг или скорость равномерного движения тела равна 5м/с). Величина – это понятие, которое позволяет выразить свойства предметов и явлений в количественном виде.
Все величины можно разделить на переменные и постоянные. Постоянная величина - это такая величина, значения которой не меняются. Так например, при равномерном движении тела его скорость не изменяется. Однако бывают и абсолютно постоянные величины - величины, которые сохраняют своё значение в любом явлении. Например, число π – отношение длины окружности к её диаметру. Переменная величина – это такая величина, значение которой меняются в процессе ее наблюдения. Например, при равномерном движении меняется координата движущегося тела. При заболевании меняется температура тела человека.
Если величина меняется, то следует говорить об области ее изменения. Определение. Совокупность всех числовых значений переменной величины называется областью изменения этой величины. Область изменения переменной величины можно представить на числовой оси совокупностью точек, в простейшем случае отрезком числовой оси или интервалом. Интервал (или промежуток) – это совокупность всех чисел x числовой оси, заключенных между данными числами a и b, при этом числа a и b не принадлежат этой совокупности. Обозначение: a < x < b, или (a, b), или x Î (a, b). Символ Î обозначает слово «принадлежит». Если числа a и b принадлежат рассматриваемой совокупности, то область изменения называют отрезком (или сегментом, замкнутым промежутком, замкнутым интервалом). Обозначение: a ≤ x ≤ b или x Î [ a, b ]. Совершенно аналогично можно ввести понятие полузамкнутого интервала, когда одно из чисел a или b принадлежит рассматриваемой совокупности, а другое нет. Обозначение: a < x ≤ b или (a,b ]. Вполне понятно, что можно ввести и бесконечные интервалы (- ¥,¥). Упорядоченная переменная величина.
Обозначим произвольную переменную величину через x. Будем говорить, что переменная x есть упорядоченная переменная величина, если известна область изменения этой переменной величины, и про каждое из двух любых ее значений можно сказать, какое значение предыдущее и какое последующее.
Определение. Переменная величина называется возрастающей, если каждое ее последующее значение больше предыдущего. Переменная величина называется убывающей, если каждое ее последующее значение меньше предыдущего.
Функция.
При изучении различных явлений часто возникает задача изучения изменения одной величины в зависимости от изменения другой. Например, как меняется успеваемость студентов в зависимости от времени, потраченного на подготовку к занятиям. В этом случае мы приходим к понятию функции.
Определение. Совокупность значений x для которых правило вычисления значений y имеет смысл, называется областью определения функции или областью существования функции, а область изменения У называется множеством значений функции.
1.5. Способы задания функции.
1. Табличный способ задания функции. При этом способе выписываются в определенном порядке значения аргумента и соответствующие значения функции.
Примером таких таблиц могут служить таблицы тригонометрических функций, таблицы логарифмов, результаты экспериментов.
2. Графический способ задания функции. Если в прямоугольной системе координат на плоскости изобразить в виде линии некоторую совокупность точек так, что
Рис. 1.
Откладывая на оси абсцисс необходимое значение x и восстанавливая перпендикуляр из точки x до пересечения с кривой, а затем, проводя прямую, параллельную оси абсцисс до пересечения ее с осью ординат, получим значение функции 3. Аналитический способ задания функции. При аналитическом способе задания функция представляется аналитическим выражением, то есть через совокупность известных математических операций, которые производятся в определенной последовательности над числами и символами, обозначающими постоянные и переменные величины. Примером аналитических выражений могут служить: Предел функции.
Функции могут иметь предел. Что же нужно понимать под пределом функции?
Для первого графика, изображенного на рисунке,
Можно дать более строгое определение предела функции: пусть функция Математическая запись предела функции: Некоторые важные пределы. 1). 2). 3). Вычисление пределов. Для вычисления пределов используют основные теоремы и правило Лопиталя (при возникновении «неопределенности» вида 0/0 или ∞∕∞), согласно которому предел частного двух функций равен пределу отношений производных этих функций:
Пример 1. Найти предел функции: Решение: Пример 2. Найти предел функции: Решение:
Пример 3. Найти предел функции: Решение:
Пример 4. Найти предел функции: Решение: Пример 5. Найти предел функции: Решение:
Пример 6. Найти предел функции: Решение: При подстановке х=0 получаем неопределенность 0/0. Тогда по правилу Лопиталя: Пример 7. Найти предел функции: Решение: При подстановке х=2 получаем неопределенность 0/0, которую раскрываем по правилу Лопиталя:
Пример 8. Найти предел функции: Решение: При подстановке х=∞ получаем неопределенность ∞∕∞, которую раскрываем по правилу Лопиталя:
Непрерывность функции.
Большинство функций, изучаемых в математическом анализе, являются непрерывными, то есть при небольших изменениях аргумента х функция у меняется также мало, и график такой функции является непрерывной кривой. Однако, у некоторых функций при определенных значениях х непрерывность может нарушаться и график прерываться, тогда говорят, что функция в данных точках имеет разрыв. Значения аргумента, при которых происходит разрыв функции, называются точками разрыва. Определение: Функция y=f(x) непрерывна в точке x0, если в этой точке у нее существует предел Определение: Функция у=f(x) называется непрерывной в интервале, если она непрерывна в каждой точке этого интервала.
Отметим, что, вычисляя предел функции f(х), мы можем приближать х к x0 как справа, так и слева, то есть вычислять Непрерывность функции в точке x0 равносильна ее непрерывности в этой точке одновременно слева и справа, то есть должны выполняться следующие четыре условия непрерывности: 1). Функция должна быть определена в некоторой окрестности точки x0. 2). Должны существовать конечные пределы слева и справа:
3). Эти пределы должны быть равны между собой и равны А:
4). Эти пределы должны быть равны значению функции в точке x0, то есть А=f(x0).
Если в точке x0 не выполняется хотя бы одно условие, то в этой точке функция терпит разрыв, а сама эта точка называется точкой разрыва. Если выполняются условия 1 и 2, но нарушены условия 3 и 4, то точку x0 называют точкой разрыва первого рода. Если хотя бы один из пределов слева или справа бесконечен или его вовсе нет, тогда говорят о разрыве второго рода. Пример: тригонометрические функции sinx и cosx непрерывны повсюду, функция tg(x) имеет разрыв второго рода в точках
Понятие производной.
Определение: Пусть имеется функция
Следует заметить, что у некоторых функций может не существовать предел отношения приращения функции к приращению аргумента в каких-то точках, то есть в этих точках такие функции производной не имеют.
Функция, имеющая конечную производную в данной точке, называется дифференцируемой в этой точке. Очевидно, что необходимым условием дифференцируемости функции является ее непрерывность. Производная любой функции может быть найдена по формуле (*). Например:
Однако, так находить производную функции слишком долго, поэтому была разработана таблица производных основных элементарных функций, которой обычно и пользуются. Таблица производных элементарных функций, свойства производных.
Нахождение производной сложной функции. В этом случае необходимо применять следующие правила, получившие название «свойства производных»: 1. Производная алгебраической суммы дифференцируемых функций равна алгебраической сумме производных этих функций: если 2. Постоянный множитель можно выносить за знак производной: если 3. Производная произведения двух функций равна сумме произведений производной первой функции на вторую и производной второй функции на первую. Если заданы функции 4. Производная частного двух функций равна дроби, числитель которой равен разности произведений производной числителя на знаменатель и производной знаменателя на числитель, а знаменатель равен квадрату знаменателя исходной дроби. Пусть функция если 5. Производная сложной функции. Если функция u =j (x) имеет производную в точке x o, а функция y=f (u) имеет производную в соответствующей точке u о = j (x o), то сложная функция f [ j (x)] имеет производную в точке x o и справедлива следующая формула: Общие понятия.
Дифференциал функции выводится из определения производной:
Применение дифференциала. Дифференциал применяется для приближенных вычислений и оценки погрешностей. Согласно определению дифференциала ∆у≈dу. Но так как Эти формулы и используют для приближенных вычислений и оценки погрешностей в случае, когда у'(х)≠0. Пример 1. Найти приращение функции Решение: Воспользуемся формулой: Пример 2. Найти приближенное значение функции Решение: Воспользуемся формулой:
Пример 3. Вычислить без помощи таблиц и калькуляторов Решение: Воспользуемся формулой: Пример 4. С какой точностью можно определить площадь поверхности сферы радиуса R=1,03 см, если радиус задан с точностью D R=0,005 см? Решение: Так как площадь сферы можно найти по формуле
Пример 5. Найти приращение функции Решение:
Пример 6. Найти приближенное значение функции Решение: Воспользуемся формулой у(х+∆х)≈у(х)+у'dx=
Пример 7. Найти без помощи таблиц Решение: Воспользуемся формулой:
Тогда Функция двух переменных.
Функция не всегда зависит от одной переменной. Например, перемещение тела определяется как его скоростью, так и временем движения. В этом случае функция будет зависеть от двух переменных. Определение: Величину z называют функцией двух независимых переменных х и у, если каждой паре допустимых значений этих величин по определенному закону соответствует одно вполне определенное значение величины z.
Множество всех допустимых пар значений аргументов х и у называют областью определения функции двух переменных. Допустимыми значениями аргументов х и у считают такие, которым соответствуют действительные значения функции z.
Пример функции двух переменных:
Множество всех допустимых пар значений аргументов х и у называют областью определения функции двух переменных. Допустимыми значениями аргументов х и у считают такие, которым соответствуют действительные значения функции z.
Решение. Выражение, стоящее справа, теряет смысл при тех значениях х и у, при которых знаменатель обращается в нуль. Отсюда областью определения нашей функции является вся плоскость, из которой выброшена прямая у=2х.
Скалярное поле.
Если в каждой точке некоторой области пространства D задана функция U(p)=U(x,y,z), то говорят, что в области D задано скалярное поле. Если, например, U(x,y,z) обозначает температуру в точке М(х,у,z), то говорят, что задано скалярное поле температур. Если область D заполнена жидкостью или газом и U(x,y,z) обозначает давление, то имеется скалярное поле давлений. Если в пространстве задано расположение зарядов или массивных тел, то говорят о поле потенциала. Скалярное поле называется стационарным, если функция U(x,y,z) не меняется со временем: U(х,у,z) ≠ f (t).
Любое стационарное поле характеризуется: 1) поверхностью уровня скалярного поля 2) скоростью изменения поля в заданном направлении. Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция U(x,y,z) принимает постоянное значение, то есть U(x,y,z) = const. Совокупность этих точек образует некоторую поверхность. Если возьмем другую константу, то получим другую поверхность.
Направление наибольшего возрастания скалярной функции задается вектором, который называется градиентом и обозначается символом Градиент функции находится через частные производные этой функции и всегда перпендикулярен поверхности уровня скалярного поля в данной точке:
Производная от функции U(x,y,z) по любому другому направлению (λ) определяется по формуле:
α, β, γ – это углы между осями координат соответственно OX, OY, OZ и направлением Производную функции по направлению можно найти и через другую формулу:
Таким образом, производная функции по данному направлению равна скалярному произведению градиента функции на единичный вектор этого направления. В этом случае, производная по направлению вектора, касательного к поверхности уровня, равна нулю, а градиент в каждой точке перпендикулярен касательной плоскости к поверхности уровня, проходящего через данную точку. Пример на нахождение градиента функции в данной точке. Пусть дана функция Определим градиент в точке М(1,1,1). Выражение градиента этой функции в произвольной точке будет:
Следовательно, Таблица основных интегралов
Методы интегрирования 1) Непосредственное интегрирование. Этот метод заключается в прямом использовании табличных интегралов и их свойств. Пример: Пример: Пример: Следует отметить, что хотя при взятии каждого интеграла появляется своя константа, однако окончательный результат выражается через одну произвольную постоянную, являющуюся их линейной комбинацией. 2) Метод разложения Этот метод заключается в разложении подынтегральной функции в линейную комбинацию более простых функций с использованием известных формул. Пример: Пример:
Пример;
3) Метод подведения под знак дифференциала. В данном методе для приведения искомого интеграла к табличному виду преобразовывают дифференциал аргумента функции. Дифференциал не меняется, если к переменной прибавить или отнять постоянную величину, а если переменную увеличить в несколько раз, то дифференциал необходимо умножить на обратную величину, то есть Пример: Пример: Пример:
4) Метод выделения полного квадрата из квадратичного трехчлена. Пример: Пример: 5) Метод замены переменных Этот метод основан на замене переменной интегрирования в неопределенном интеграле. Основная цель - свести его нахождение к нахождению такого определенного интеграла, который может быть найден методом разложения. Замечание. Подведение под знак дифференциала является частным случаем замены переменной, так как выполняются те же действия, только не вводится новая переменная. Пример: ∫ Введем новую переменную z=x+2. Найдем из этого уравнения связь между дифференциалами старой и новой переменной. Для этого продифференцируем левую и правую часть уравнения z=x+2. Получим: dz=dx. Тогда наш интеграл примет вид:
Пример: Если внимательно посмотреть на числитель и знаменатель подынтегрального выражения, то можно заметить, что числитель с точностью до постоянного множителя представляет собой дифференциал знаменателя. Тогда можно ввести новую переменную z=x
Перейдя к старой переменной в конечном результате, получим искомое решение интеграла. Пример: Введем замену переменной: Подставим замену в исходное выражение и возьмем интеграл:
Пример: Введем замену переменной: Продифференцируем данное выражение: Выразим dx через dz. Получим: Подставим замену в исходное выражение и возьмем интеграл:
Пример: Введем замену u=cosx. Продифференцируем данное выражение: du= -sinx∙dx. Выразим du через dx, подставим в исходное выражение и возьмем интеграл:
Пример: Используем подстановку u=sinx и du=cosx∙dx. Тогда
6) Интегрирование по частям. Этот метод основан на использовании формулы интегрирования по частям:
1) Интегралы вида Р(х)- многочлен решаются по частям при замене dv=P(x)dx, и u – другие сомножители. Пример: Подынтегральное выражение подставим виде udv. Через u следует обозначить lnx, а через dv=xdx. Тогда du= Пример: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

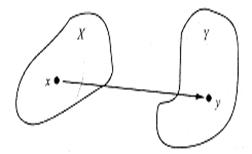 Определение. Если каждому значению одной переменной величины x, принадлежащему некоторой области изменения, по некоторому правилу можно поставить в соответствие одно или несколько значений другой переменной величины y, то говорят, что задана функция y от x:
Определение. Если каждому значению одной переменной величины x, принадлежащему некоторой области изменения, по некоторому правилу можно поставить в соответствие одно или несколько значений другой переменной величины y, то говорят, что задана функция y от x: 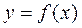 , где f есть некоторое правило, а х носит названиеаргумента функции.
, где f есть некоторое правило, а х носит названиеаргумента функции.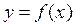 , где x – абсциссы точек, а y – ординаты, то такая совокупность точек называется графиком функции (рис. 1).
, где x – абсциссы точек, а y – ординаты, то такая совокупность точек называется графиком функции (рис. 1).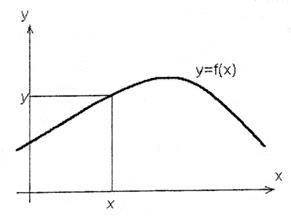
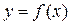 в точке x.
в точке x.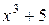 ,
, 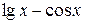 .
. Определение: Функция у=f(x) имеет предел А при х→а, если при приближении х к а значение функции как угодно близко подходит к А, то есть
Определение: Функция у=f(x) имеет предел А при х→а, если при приближении х к а значение функции как угодно близко подходит к А, то есть  .
. , а для второго
, а для второго  .
. определена в некоторой области, включающей точку а. Говорят, что
определена в некоторой области, включающей точку а. Говорят, что  .
.
 , если х – длина дуги или угол, выраженный в радианах.
, если х – длина дуги или угол, выраженный в радианах.
 , при условии, что этот предел существует. Если после использования этого правила снова возникает неопределенность, то его применяют вторично.
, при условии, что этот предел существует. Если после использования этого правила снова возникает неопределенность, то его применяют вторично. .
. .
. .
. .
. .
.
 .
. .
. .
.
 .
. .
. .
. .
. .
. .
. .
. и
и  .
. ,
,  .
. =
=  = А.
= А. , где k=0; ±1; ±2…., а функция ctg(x) имеет разрыв второго рода в точках
, где k=0; ±1; ±2…., а функция ctg(x) имеет разрыв второго рода в точках  , где k=0; ±1; ±2….
, где k=0; ±1; ±2…. . Тогда, производной функции у по переменной х называется предел отношения приращения этой функции к приращению аргумента при стремлении последнего к нулю:
. Тогда, производной функции у по переменной х называется предел отношения приращения этой функции к приращению аргумента при стремлении последнего к нулю: (*).
(*). . Тогда:
. Тогда:









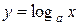







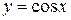













 , то
, то  .
. , то
, то  .
. и
и  , то
, то  .
. представляет собой отношение двух дифференцируемых функций
представляет собой отношение двух дифференцируемых функций  , то
, то 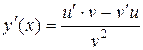 .
. . Таким образом, при нахождении производной сложной функции необходимо ввести промежуточный аргумент u= j (x), позволяющий свести данную функцию к виду основных элементарных функций f [ j (x)]=f(u), взять производную этой функции (в соответствии с таблицей производных), а затем умножить ее на производную от промежуточного аргумента.
. Таким образом, при нахождении производной сложной функции необходимо ввести промежуточный аргумент u= j (x), позволяющий свести данную функцию к виду основных элементарных функций f [ j (x)]=f(u), взять производную этой функции (в соответствии с таблицей производных), а затем умножить ее на производную от промежуточного аргумента. . Следовательно,
. Следовательно,  , где β – бесконечно малое число. Отсюда можно найти ∆у:
, где β – бесконечно малое число. Отсюда можно найти ∆у:  . Последнее слагаемое в этом выражении имеет второй порядок малости, поэтому первое слагаемое главным образом и определяет величину приращения функции и поэтому называется главной линейной частью приращения функции или ее дифференциалом и обозначается dy:
. Последнее слагаемое в этом выражении имеет второй порядок малости, поэтому первое слагаемое главным образом и определяет величину приращения функции и поэтому называется главной линейной частью приращения функции или ее дифференциалом и обозначается dy:  .
. , а
, а  , следовательно, у(х+∆х)-у(х)≈у'(х)dx или у(х+∆х)≈у(х)+у'(х)dx.
, следовательно, у(х+∆х)-у(х)≈у'(х)dx или у(х+∆х)≈у(х)+у'(х)dx. , если ее аргумент изменяется от 1 до 1,001.
, если ее аргумент изменяется от 1 до 1,001. , тогда
, тогда  . Подставим в полученную формулу значения х=1 и ∆х=0,001 и найдем ∆у:
. Подставим в полученную формулу значения х=1 и ∆х=0,001 и найдем ∆у:  .
. при s= 2,001.
при s= 2,001. . Так как
. Так как , то
, то
 .
. , х=81, а ∆х=8. Согласно формуле:
, х=81, а ∆х=8. Согласно формуле: 
 , то
, то 
 .
. , если аргумент изменяется от 2 до 2,001.
, если аргумент изменяется от 2 до 2,001. .
. при аргументе, равном 3,02.
при аргументе, равном 3,02. .
. .
. , х=16, а ∆х=3.
, х=16, а ∆х=3. .
. Аналитически такую функциональную зависимость обозначают: z=f(x,y).
Аналитически такую функциональную зависимость обозначают: z=f(x,y). . Графиком такой функции является круговая парабола (см. рисунок).
. Графиком такой функции является круговая парабола (см. рисунок). Пример: Найти область определения функции
Пример: Найти область определения функции  .
. Пример: Пусть задано скалярное поле
Пример: Пусть задано скалярное поле  . Примером такого поля является поле электрического потенциала точечного электрического заряда (+q). Здесь поверхностями уровня будут эквипотенциальные поверхности
. Примером такого поля является поле электрического потенциала точечного электрического заряда (+q). Здесь поверхностями уровня будут эквипотенциальные поверхности  , то есть сферы, в центре которых находится заряд, создающий поле.
, то есть сферы, в центре которых находится заряд, создающий поле. (или
(или  ).
). , где
, где

 - единичные векторы соответственно по осям OX, OY, OZ
- единичные векторы соответственно по осям OX, OY, OZ , где
, где .
.
 , где
, где  .
. .
. .
. ,
,  .
.










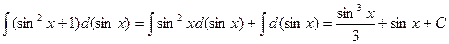




 .
.

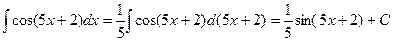


 .
. .
. =
=  =ln│z│+c= ln│x+2│+c
=ln│z│+c= ln│x+2│+c .
. +7. Тогда связь между dz и dx можно найти из последнего выражения, продифференцировав левую и правую его части: dz=2x∙dx. Тогда наш интеграл примет вид табличного интеграла:
+7. Тогда связь между dz и dx можно найти из последнего выражения, продифференцировав левую и правую его части: dz=2x∙dx. Тогда наш интеграл примет вид табличного интеграла: =
= 

 , так, чтобы избавиться от квадратного корня в знаменателе. Тогда
, так, чтобы избавиться от квадратного корня в знаменателе. Тогда  . Затем продифференцируем данное выражение:
. Затем продифференцируем данное выражение:  . Значит,
. Значит,  .
.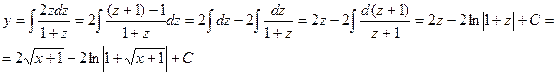

 .
. .
. .
.
 .
. = -
= -  = -ln│u│+c= - ln│cosx│+c
= -ln│u│+c= - ln│cosx│+c .
. =
=  =
= 
 , где u(x) и v(x) – функции, имеющие непрерывные производные в некотором промежутке. При использовании данной формулы нахождение исходного интеграла
, где u(x) и v(x) – функции, имеющие непрерывные производные в некотором промежутке. При использовании данной формулы нахождение исходного интеграла  сводится к нахождению интеграла
сводится к нахождению интеграла 
 , причем эту процедуру имеет смысл проводить лишь в том случае, если новый интеграл проще исходного и может быть найден с использованием рассмотренных выше способов интегрирования.
, причем эту процедуру имеет смысл проводить лишь в том случае, если новый интеграл проще исходного и может быть найден с использованием рассмотренных выше способов интегрирования. ,
,  ,
,  , где
, где
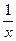 dx, а v=
dx, а v=  . Согласно формуле интегрирования по частям:
. Согласно формуле интегрирования по частям: 



