
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра физики и высшей математикиСтр 1 из 3Следующая ⇒
Кафедра физики и высшей математики Физ.мат-16.03.0604.зчн.плн Физ.мат-16.03.0605.зчн.плн Физ.мат-16.03.0606.зчн.плн Физ.мат-16.03.0608.зчн.плн Физ.мат-16.03.0611.зчн.плн Физ.мат-16.03.3510.зчн.плн Физ.мат-16.03.3513.зчн.плн Высшая математика
Часть 1
Москва 2005
СОДЕРЖАНИЕ
Стр.
1. Предисловие…………………………………………………… 2. Рабочая программа курса «Математика» для студентов экономических специальностей высших учебных заведений………………………………...…… 3. Учебная литература ………………………………………..…. 4. Методические указания к решению задач ……………….….. 5. Задачи для контрольных работ …………………………….… 5.1. Раздел I. Линейная алгебра. Аналитическая геометрия ………………………………. 5.2. Раздел II. Дифференциальное и интегральное исчисление. Дифференциальные уравнения. Ряды ………………….. 6. Таблица распределения задач по вариантам и контрольным работам …………………………………….… 7. Правила выполнения и оформления контрольных работ …..
Предисловие Математика – это наука о пространственных формах и количественных отношениях в самом общем виде, - прошла большой путь развития одновременно с развитием цивилизации и стала неотъемлемой частью культуры человечества и показателем интеллектуального уровня общества. Помимо собственных потребностей развития математика обслуживает потребности многих других наук – естественных, технических, экономических, гуманитарных. С развитием вычислительной техники область использования математики расширяется. В наше время трудно представить себе хорошего специалиста в области экономики, не знающего основных математических методов и математического языка. Поэтому математика включена в учебные планы всех экономических специальностей и ее изучению отводится немало времени. Для успешного изучения математики необходимы программа, учебники и учебные пособия, справочная литература, таблицы, инженерный микрокалькулятор и, конечно, волевые усилия. Необходимо посещать все очные занятия в период сессий и стремиться самостоятельно, выполнять контрольные работы, пользуясь руководствами к решению задач, методическими указаниями и конспектами практических занятий.
Предлагаемые «Методические указания» должны помочь студенту-заочнику рационально организовать свой труд по изучению математики и выполнению контрольных работ. Они выйдут в двух частях. Часть 1 предназначена для выполнения контрольной работы № 1, часть 2 – для контрольной работы № 2. Обратите пристальное внимание, на таблицу распределения задач по вариантам и в соответствии с ней выполняйте работы. Желаем Вам успеха.
Авторы
2. РАБОЧАЯ ПРОГРАММА КУРСА «МАТЕМАТИКА» ДЛЯ СТУДЕНТОВ ЭКОНОМИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ І. Элементы линейной алгебры. 1. Матрицы. Виды матриц. Действия над матрицами, свойства матриц. Обратная матрица. Определители, их свойства. Вычисление определителей. 2. Системы линейных уравнений. Метод Гаусса, правило Крамера. Ранг матрицы, теорема Кронекера - Капелли. Квадратичные формы. 3. Понятие о задаче линейного программирования и симплекс – методе. ІІ. Элементы векторной алгебры и аналитическая геометрия плоскости. 1. Системы координат на плоскости. Векторы. Линейные операции над векторами. Линейная зависимость векторов. Базис, координаты вектора в данном базисе. Скалярное произведение векторов. Уравнения прямых на плоскости. Кривые второго порядка. ІІІ. Математический анализ. 1. Функции, пределы, бесконечно малые и бесконечно большие. 2. Производная и дифференциал. Приложение к исследованию функций. Правило Лопиталя. 3. Функции нескольких переменных. Частные производные, полный дифференциал. Экстремумы функции нескольких переменных. 4. Неопределенный интеграл. Интегрирование методом подстановки, интегрирование по частям. Интегрирование тригонометрических функций. Определенный интеграл. Формула Ньютона-Лейбница. Несобственный с бесконечными пределами. ІV. Ряды. 1. Числовые ряды. Необходимый и достаточные признаки сходимости. Знакопеременные ряды, абсолютная и условная сходимость. Признак Лейбница. 2. Ряд Тейлора. Разложение функции в степенной ряд. Понятие о тригонометрических рядах.
V. Дифференциальные уравнения. 1. Уравнение первого порядка с разделяющимися переменными. 2. Однородные и линейные уравнения первого порядка. VI. Элементы комбинаторного анализа. 1. Перестановки, размещение и сочетания. 2. Методы подсчета числа объектов и конфигураций. VII. Теория вероятностей. 1. Классическое определение вероятности. 2. Алгебра событий. 3. Формула полной вероятности и Байеса. 4. Повторение испытаний. Схема Бернулли, теоремы Муавра-Лапласа и Пуассона. 5. Случайные величины (дискретные и непрерывные). Законы распределения: равномерное, нормальное. Числовые характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение. 6. Центральная предельная теорема. VIII. Математическая статистика. 1. Выборочный метод. Репрезентативность выборки. Эмпирическая функция распределения. Полигон и гистограмма. 2. Выборочное среднее и дисперсия. 3. Интервальные оценки. Правило трех сигм. 4. Проверка статистических гипотез. Сравнение математических ожиданий двух распределений. Однофакторный дисперсионный анализ. 5. Проверка репрезентативности выборки. Критерий согласия Х2 («хи-квадрат»). 6. Элементы теории корреляции. Коэффициент линейной корреляции. Криволинейная множественная корреляция. 7. Дискретная математика. Элементы теории графов (транспортная задача). Элементы комбинаторного анализа и блок–схемы (план эксперимента).
УЧЕБНАЯ ЛИТЕРАТУРА а) Основная. 1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М., Наука, 1984. 2. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. ФПК. – М., Наука, 1985. 3. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – М., Наука, 1988. 4. Высшая математика для экономистов. Под ред. проф. Н.Ш. Кремера. изд. 2-ое. – М., Банки и биржи, 1998. 5. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики.- М., 1985. 6. Бугров Я.С., Никольский С.М. Высшая математика. Задачник. – М., Наука, 1982. 7. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. Ч.1, - М., Финансы и статистика, 1998.
б) Дополнительная 1. Баврин И.И. Курс высшей математики. Учебник. – М., Просвещение, 1992. 2. Беклемишева Л.А., Петрович Ю.А., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре. – М., Наука, 1987. 3. Бутузов В.Ф. др. Математический анализ в вопросах и задачах. – М., Высшая школа, 1993. 4. Краснов М.Л., Обыкновенные дифференциальные уравнения. М., Высшая школа, 1983. 5. Кузнецов Л.А. Сборник задач по высшей математике. - М., Высшая школа, 1991 (уч. пособие). 6. Лотов А.В. Введение в экономико-математическое моделирование. - М., Наука, 1984. 7. Мысовских И.П. Лекции по методам вычислений, 2-ое изд., - М., Наука 1994. 8. Рябенький В.С. Введение в вычислительную математику. - М., Наука,1993.
в) Устанавливаемая кафедрой (приводится литература, имеющаяся в библиотеке МГТА) 1. Карасев А.И., Аксютина З.И., Савельева Т.И. Курс высшей математики для экономических вузов. - М., Высшая школа (ВШ) 1982, ч.1; 1983, ч.2. 2. Маркович Э.С. Курс высшей математики с элементами теории вероятностей и математической статистики. - М., ВШ, 1972. 3. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. - М., ВШ, 1975, 1985.
4. Пискунов Н.С. Дифференциальное и интегральное исчисление для вузов. т. 1-3, - М., Наука, 1985. 5. Ефимов Н.В. Краткий курс аналитической геометрии. - М., Наука,1972. 6. Кузнецов Ю.Н., Кутузов В.И., Волошенко А.В. Математическое программирование. - М., ВШ, 1980. 7. Данко П.Е. и др. Высшая математика в упражнениях и задачах. Ч. 1 и 2, - М., ВШ, 1986. 8. Кручкович Г.И. и др. Сборник задач по высшей математике (с решениями). Изд. 3-е. - М., Наука 1973. 9. Запорожец Г.И. Руководство к решению задач по математическому анализу. - М., ВШ, 1962, 1964 и др. г. 10. Бараненков Г.С. Задачи и упражнения по математическому анализу для вузов. - М., 1971, 1974. 11. Лихолетов И.И., Мацкевич И.П. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике. - М., ВШ, 1969. 12. Лысенко В.И. Высшая математика. Лекции для студентов высших учебных заведений, обучающихся заочно по экономических специальностям. - М., МГТА, 1999.
Решение. Система n линейных уравнений с n неизвестными является совместной и имеет единственное решение, так как определитель системы, составленный из коэффициентов при неизвестных не равен нулю. Вычислим определитель системы методом разложения его по элементом строки. Разложим по первой строке:
Так как определитель системы не равен нулю, система уравнений совместна и имеет единственное решение. а) Найдем решение системы по формулам Крамера
где D1 D2 D3 - определители, которые получаются из определителя D системы путем замены в нем соответственно 1-го, 2-го, 3-го столбцов коэффициентов при неизвестных x1 x2 x3 столбцом свободных членов уравнений, стоящих в правой части данной системы. Получим следующие три определителя:
Вычислить неизвестные Проверим это решение, подставив значения неизвестных во все уравнения системы. Получим
б) Решим ту же систему уравнений методом Гаусса. Для этого выпишем расширенную матрицу системы и приведем основную матрицу системы к треугольному виду или ступенчатому виду, если число уравнений окажется меньшим числа неизвестных. Приведение матрицы к треугольному виду, то есть такому, когда ниже (или выше) главной диагонали все элементы будут нулевые, а на главной диагонали - ненулевые, всегда возможно. Оно основано на следующих элементарных преобразованиях матрицы, соответствующих эквивалентным преобразованиям система:
1. Перестановка строк матрицы; 2. Перестановка столбцов; 3. Умножение всех элементов строки на одно и то же число; 4. Сложение элементов любой строки с соответствующими элементами любой другой строки; 5. Вычеркивание получившихся нулевых строк.
Вот решение одной системы методом последовательных исключений неизвестных:
Расширенная матрица 1-й шаг 2-шаг
Возвратимся теперь от матричной записи к системе уравнений. Из последней строки матрицы следует уравнение Существует модифицированный метод Гаусса, так называемый метод полного исключения неизвестных, в результате которого основная матрица системы преобразуется в каноническую матрицу, на главной диагонали которой остаются единицы, а все остальные элементы обращаются в нули. Таким образом сразу получается решение. В основе этого метода лежит следующий алгоритм (строго определенный порядок действий) 1. Выберем разрешающую строку и в ней разрешающий элемент. Обычно это первый элемент первой строки, считая слева направо. Строки можно целиком переставлять, так что на первое место можно записать любую строку, в которой первый элемент не равен нулю. 2. Каждый элемент, разрешающий строки разделим на разрешающий элемент. 3. Элементы разрешающего столбца заменим нулями во всех строках матрицы, кроме разрешающей, где он буден равен единице. 4. Элементы столбцов, Которые были разрешающими на предыдущих шагах исключения, переписываем без изменения. 5. Остальные элементы пересчитаем по следующему правилу «прямоугольника»:
Где П – пересчитываемый элемент, Р – Разрешающий, D1 и D2 – “диагональные”, И – искомый. Все эти элементы каждый раз должны быть вершинами воображаемого прямоугольника, образованного параллельными строками и столбцами. Искомый элемент записываем на месте пересчитываемого. Вернемся к расширенной матрице данной системы и выполним эквивалентной преобразования по предложенной выше схеме полного исключения неизвестных. Рекомендуем читателю все пересчеты коэффициентов по правилу «четырехугольника» записывать подробно.
Данная расширенная матрица 1-й шаг 2-й шаг
3 - й шаг 4 – й шаг
Если в последней матрице вернуться к записи уравнений, то получим
Замечания: 1. Кружками обведены разрешающие элементы. 2. При переходе от 2-го шага к 3-му третью строку почленно разделили на 90/7. в) Решить данную систему методом обратной матрицы. Решение. Данную систему можно записать в матричном виде АХ = В, где Решение матричного уравнения имеет вид Х = А-1 В = N, где А-1 – матрица, обратная матрицы А. Так как определитель матрицы системы D(A) = 180 отличен от нуля то матрица А имеет обратную. Для вычисления обратной матрицы воспользуемся формулой
Где А11, А12, …, А33 – алгебраические дополнения элементов а11, а12, …, а33 матрицы А. Вычислим алгебраические дополнения всех элементов матрицы А:
Составим обратную матрицу
Найдем теперь матрицу Х.
Из равенства матриц Х = N или х1=2, х2 = 1, х3 = -3.
Задача 2. Методом исключения неизвестных найти общее и базисное решение системы линейных уравнений Решение.
Это система двух уравнений с тремя неизвестными. Она совместна и неопределенна. Надо описать совокупность всех ее решений. В качестве базисных неизвестных данной системы можно взять те неизвестные, для которых определитель составленный из коэффициентов при нет известных, не равен нулю. Здесь три таких определителя, один из которых равен нулю Или в матричной форме Общее решение: Полагая в общем решении х3 = 0, получим базисное решение х1 = Проверка базисного решения показывает, что оно удовлетворяет обоим уравнениям системы, то есть, является частным решением системы. Давая х3 любые другие числовые значения, получим бесчисленное множество частных решений. Аналогично решаются системы с несколькими свободными неизвестными.
Задача 3. Даны матрицы произведение матриц АВ. Решение. Эти матрицы являются соответственными, так как число столбцов первой матрицы равно числу строк второй: их размеры
Задача 4. Даны вершины треугольника А(-3;-2), В(1;8), С(5;3). Найти: а) уравнения всех трех его сторон; б) систему неравенств, определяющих множество точек, принадлежащих треугольнику, включая его стороны; в) внутренний угол А треугольника в градусах и минусах; г) длину высоты, опущенной из вершины А; д) площадь треугольника. Решение. а) Уравнения сторон найдем по формуле прямой, проходящей через две данные точки Уравнение стороны АВ:
Уравнение стороны АС:
б) Каждая из прямых, уравнения которых только это найдены, разделяет плоскость на две полуплоскости, определяемые соответствующими неравенствами.
Рис. 1.
Система неравенств в) Внутренний угол треугольника найдем, зная угловые коэффициенты сторон АВ и АС, образующих этот угол, по формуле Угловые коэффициенты прямых выложим по формуле Получим Тогда
г) Длину высоты AD^BC (рис. 1) найдем как расстояние от данной точки А(-3;-2) до данной прямой ВС: 5х + 4у – 37 = 0 по формуле
Получим
д) Площадь треугольника можно вычислить несколькими способами. Вычислить ее через координаты вершин треугольника по формуле Получим Итак, площадь треугольника SABC = 30 кв. ед.
Задачи раздела ΙΙ заданий (см. оглавление, п.5.2) Задача 5. Найти производные сложные и неявная функции): а)
Решение. Решение. Решение. Дифференцируем как сложную функцию.
г)
Решение.
Задача 6. С помощью правила Лопиталя вычислить пределы функций: 1) Решение. Непосредственная подстановка х = 0 приводит к неопределенности вида
2)
Решение. При
Задача 7. Исследовать функцию Решение.
Исследование выполним по примерной схеме, имеющейся в учебниках и практических руководствах. График можно строить либо по ходу исследования, либо конце исследования (рис.2).
Вертикальная асимптота может быть в точке разрыва или на границе области определения. Здесь вертикальная асимптота Здесь Итак,
5) Найти интервалы монотонности (возрастания и убывания) функции и точки экстремума. Найдем производную первого порядка.
Найдем критические точки первого рода и выясним знаки
Возьмем интервал
Итак, функция возрастает на интервалах
6) Найти интервалы выпуклости и вогнутости графика функции и точки перегиба. Вычислим производную второго порядка и найдем критические точки второго рода.
Задача 8. Три пункта А.В. и С расположены так, что угол АВС (рис.3) равен 600. Расстояние между пунктами А и В равно 200 км. Одновременно из пункта А выходит автомобиль, а из пункта В – поезд. Автомобиль движется по направлению к пункту В со стороны 80 км/ч, а поезд движется по направлению к пункту С со скоростью 50 км/ч. Через скорость времени расстояние между автомобилем и поездом будет наименьшим? Решение.
рис. 3.
Тогда получим уравнение
Отсюда
Квадратный трехчлен под корнем в знаменателе в ноль не обращается ни при каких действительных значениях t, поскольку его дискриминант Д Легко видеть, что при переходе через критическую точку t0 от меньших значений t к большим, например, от t = 1 до t = 2, первая производная меняет знак с минуса на плюс
Задача 9. Найти частные производные и полный дифференциал функции двух независимых переменных: а) Решение. Найти частные производные Получим б) Решение. Найдем частные производные
Составим полный дифференциал
Задача 10. Найти экстремум функции Решение. Найдем частные производные: и смешанную производную Необходимое условие экстремума: Решим систему уравнений x = -9 Итак, точка P(-9; -3) критическая точка. Составим выражение а если Если Установим характер экстремума в точке P(-9; -3).
Задача 11. Найти неопределенные интегралы а) в) Предлагаемые интегралы можно, применив основные методы интегрирования; метод замены переменной подстановка, метод интегрирования по частям. Решение. а) Подстановка: или б) В первом из интегралов, стоящих справа, введем подстановку Второй интеграл справа является табличным Итак, в) Подстановка: Получим табличный интеграл типа г) Примем В первом из этих двух равенств обе части дифференцируем, чтобы найти Применив формулу интегрирования по частям, получим
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 203; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.171.121 (0.222 с.) |
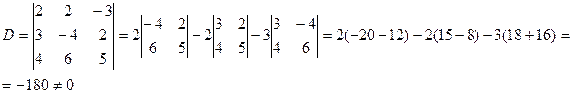
 ,
,  ,
,  ,
,


 ,
,  ,
,  .
. Решение верное.
Решение верное.
 , откуда х3 = -3 Подставляя х3 = -3 в последнее уравнение (вторая строка расширенной матрицы) получим
, откуда х3 = -3 Подставляя х3 = -3 в последнее уравнение (вторая строка расширенной матрицы) получим  или
или  . Наконец, из первого уравнения системы (первая строка матрицы) найдем
. Наконец, из первого уравнения системы (первая строка матрицы) найдем  Решение
Решение  такое же, как в случае (а). Оно уже проверено.
такое же, как в случае (а). Оно уже проверено.

 РD2
D1 П
РD2
D1 П


 ,
,  ,
,  , а это и есть решение данной системы.
, а это и есть решение данной системы. ,
,  ,
, 

 ;
;  ;
;  ;
; ;
;  ;
; 
 ;
;  ;
;  .
.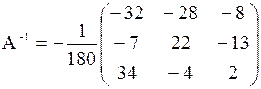 .
.
 следует решение системы
следует решение системы
 . Следовательно, неизвестные х1 и х2 нельзя брать в качестве базисных. Примем за базисные неизвестные х1 и х2, для которых определитель
. Следовательно, неизвестные х1 и х2 нельзя брать в качестве базисных. Примем за базисные неизвестные х1 и х2, для которых определитель  . Будем считать неизвестную х3 свободной и запишем систему в виде
. Будем считать неизвестную х3 свободной и запишем систему в виде 
 . Воспользуемся методом полного исключения неизвестных:
. Воспользуемся методом полного исключения неизвестных: 

 ,
, 
 и
и  . Найти
. Найти и
и  . В результате умножения матриц получим новую матрицу С размера
. В результате умножения матриц получим новую матрицу С размера  , а ее элементы будут равны скалярным произведениям векторов-строк первой матрицы на векторы-столбцов второй:
, а ее элементы будут равны скалярным произведениям векторов-строк первой матрицы на векторы-столбцов второй:

 , или
, или  (АВ).
(АВ). или
или  (АС)
(АС)






 Чтобы определить знаки этих неравенств, возьмем координаты какой-нибудь точки заведомо расположенной внутри треугольника АВС (см. рисунок 1). Такой точкой является, например точка N (0;1) подставляя координаты этой точки в уравнения граничных прямых (сторон) в силу того, что точка N не лежит ни на одной сторон, получим следующую систему неравенств.
Чтобы определить знаки этих неравенств, возьмем координаты какой-нибудь точки заведомо расположенной внутри треугольника АВС (см. рисунок 1). Такой точкой является, например точка N (0;1) подставляя координаты этой точки в уравнения граничных прямых (сторон) в силу того, что точка N не лежит ни на одной сторон, получим следующую систему неравенств.  определяющих множество внутренних точек треугольника.
определяющих множество внутренних точек треугольника. определяет множество точек, принадлежащих треугольнику АВС, включая его стороны.
определяет множество точек, принадлежащих треугольнику АВС, включая его стороны. .
. .
. ;
;  .
.
 . Угол определяем с помощью таблицы тангенсов или калькулятора
. Угол определяем с помощью таблицы тангенсов или калькулятора , где А, В, С – коэффициенты прямой,
, где А, В, С – коэффициенты прямой,  - координаты данной точки.
- координаты данной точки. (мин. ед.)
(мин. ед.) .
. .
. следующих функций (дается
следующих функций (дается

 . Это неявная функция.
. Это неявная функция.
 ,
,  ,
,  .
. .
. , следовательно, можно применить правило Лопиталя: заменить предел отношения функций пределом отношения их производных.
, следовательно, можно применить правило Лопиталя: заменить предел отношения функций пределом отношения их производных.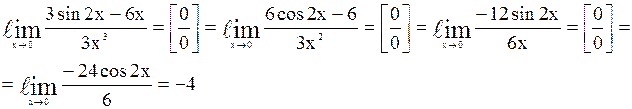

 получим неопределенность вида
получим неопределенность вида  , когда можно применить правило Лопиталя.
, когда можно применить правило Лопиталя.

 и построить ее график.
и построить ее график.





 Область определения функции
Область определения функции
 .
2) Найдем точки пересечения графика функции с осями координат. Пусть
.
2) Найдем точки пересечения графика функции с осями координат. Пусть  , тогда
, тогда  . Пусть
. Пусть  или
или  . Значит, график функции проходит через начало координат.
3) Проверить является ли функция четной, нечетной, общего вида.
. Значит, график функции проходит через начало координат.
3) Проверить является ли функция четной, нечетной, общего вида.
 .
Функция общего вида.
4) Найти асимптоты графика функции (вертикальные, наклонные, горизонтальные).
.
Функция общего вида.
4) Найти асимптоты графика функции (вертикальные, наклонные, горизонтальные).


 .
.  , - предел слева в точке
, - предел слева в точке  - предел справа. Наклонные асимптоты вида
- предел справа. Наклонные асимптоты вида  Найдем, если существуют конечные пределы
Найдем, если существуют конечные пределы 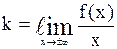 и
и  .
.
 - уравнение наклонной асимптоты.
- уравнение наклонной асимптоты.
 на полученных интервалах в окрестности критических точек. Критические точки: х1 = 0, х2 = 3, х3 = 1 - последняя н входит в область определения функции. Используя достаточные признаки экстремума, выясним, как меняет знак
на полученных интервалах в окрестности критических точек. Критические точки: х1 = 0, х2 = 3, х3 = 1 - последняя н входит в область определения функции. Используя достаточные признаки экстремума, выясним, как меняет знак  , содержащий точку
, содержащий точку  ;
;  . Так как при переходе через точку
. Так как при переходе через точку 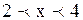 , содержащий точку х = 3.
, содержащий точку х = 3. ;
;  . Здесь производная меняет знак с «-» на «+», значит, х =3 – точка минимума функции
. Здесь производная меняет знак с «-» на «+», значит, х =3 – точка минимума функции  .
. и
и  , убывает на интервале (1;3).
, убывает на интервале (1;3). Критические точки второго рода, при которых
Критические точки второго рода, при которых  в нуль или существует, такие
в нуль или существует, такие  ,
,  , но эта последняя не входит в область определения функции. Остается точка х = 0. Проверим меняет ли знак
, но эта последняя не входит в область определения функции. Остается точка х = 0. Проверим меняет ли знак  при переходе через эту точку. Возьмем интервал (-1;
при переходе через эту точку. Возьмем интервал (-1;  ), содержащий точку х = 0. Вычислим
), содержащий точку х = 0. Вычислим  ,
,  . Отсюда следует, что х = 0 – точка перегиба,
. Отсюда следует, что х = 0 – точка перегиба, 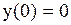 .
.  . Отсюда следует, что
. Отсюда следует, что  - интервал выпуклости;
- интервал выпуклости;  ,
,  - интервалы вогнутости кривой.
- интервалы вогнутости кривой.
 H0 MB = 200 – 80t,
NB = 50t,
cos600 =
H0 MB = 200 – 80t,
NB = 50t,
cos600 =  .
.
 ;
; км.
км. . Найдем первую производную по t:
. Найдем первую производную по t: . Приравнивая первую производную к нулю получим
. Приравнивая первую производную к нулю получим  откуда
откуда  или
или  - критическая точка.
- критическая точка. .
. . Следовательно, t0 = 1.6279 часа – точка минимума функции s. А так как других экстремумов эта функция не имеет, то в точке минимума функция имеет наименьшее значение:
. Следовательно, t0 = 1.6279 часа – точка минимума функции s. А так как других экстремумов эта функция не имеет, то в точке минимума функция имеет наименьшее значение:  .
.
 ;
;  . Составим полный дифференциал по формуле
. Составим полный дифференциал по формуле  .
. .
. .
.
 .
. .
.


 .
. и
и 
 x = 2y, 4y – y = -9, y = -3
x = 2y, 4y – y = -9, y = -3 и вычислим его значение в критической точке P(-9; -3). Тогда, если
и вычислим его значение в критической точке P(-9; -3). Тогда, если  , то P- точка экстремума. При этом, если
, то P- точка экстремума. При этом, если  , то Р – точка минимума,
, то Р – точка минимума, , то Р – точка максимума,
, то Р – точка максимума, , экстремума нет, а если
, экстремума нет, а если  - экстремум может быть, а может не быть. Нужны дополнительные исследования.
- экстремум может быть, а может не быть. Нужны дополнительные исследования. , следовательно, P(-9; -3)- точка экстремума, а так как
, следовательно, P(-9; -3)- точка экстремума, а так как  независимо от координат точки Р, то P(-9; -3) – точка минимума данной функции.
независимо от координат точки Р, то P(-9; -3) – точка минимума данной функции. , б)
, б)  ,
, , г)
, г)  , д)
, д)  .
. . Найдем дифференциалы обеих частей подстановки
. Найдем дифференциалы обеих частей подстановки 
 . Произведем замену переменной в подынтегральном выражении и найдем интеграл
. Произведем замену переменной в подынтегральном выражении и найдем интеграл  .
. .
. . откуда
. откуда  или
или  . Таким образом,
. Таким образом,  .
. .
. , где
, где 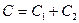 , две произвольные постоянные суммы неопределенных интегралов объединяют в одну.
, две произвольные постоянные суммы неопределенных интегралов объединяют в одну.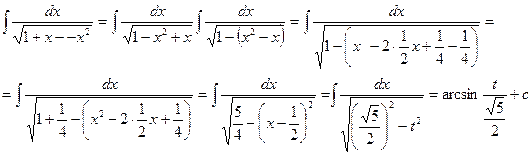

 . Возвращаясь к прежней переменной, будем иметь
. Возвращаясь к прежней переменной, будем иметь  .
. .
. ,
,  .
. , а во втором интегрируем, чтобы найти
, а во втором интегрируем, чтобы найти  . Получим
. Получим  ,
,  (здесь произвольную постоянную интегрирования принимаем равной нулю, поскольку достаточно хотя бы одного значения
(здесь произвольную постоянную интегрирования принимаем равной нулю, поскольку достаточно хотя бы одного значения  ).
). .
.


