
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементарные функции. Свойства функций.Содержание книги
Поиск на нашем сайте
К основным элементарным функциям относятся: 1. Степенная функция: 2. Показательная функция: 3. Логарифмическая функция: 4. Тригонометрические функции: 5. Обратные тригонометрические функции: Кроме основных элементарных функций к элементарным относятся функции, полученные из последних путем конечного числа операций сложения, вычитания, умножения и деления функции на функцию, а также взятия функции от функции (или сложные функции): Вспомним область определения и графики основных элементарных функций: Степенная функция. а) а – целое положительное число. Область определения (-∞, ∞). Примерный вид функции на рис.2 и рис.3.
Рис.2. Рис.3. б) а – целое отрицательное число. Функция определена для всех х за исключением т. х =0. Примерный вид функции показан на рис.4 и рис.5.
Рис.4. Рис.5. Приведем также примеры степенных функций при дробно-рациональных значениях а (рис. 6,7,8).
Рис.6. Рис.7. Рис.8. Показательная функция: Она определена при всех значениях х. Пример функции показан на рис.9.
Рис.9. Логарифмическая функция: Область определения функции (0, ∞). График функции показан на рис.10.
Рис.10. Тригонометрические функции. Графики этих функций показаны на рис. 11, 12, 13, 14.
Рис.11. Рис.12.
Рис. 13. Рис.14. Функции Исходя из графиков, мы видим, что функции бывают периодические и непериодические. Определение: Функция
Наименьшее такое число Т называется периодом функции. Все тригонометрические функции – периодические. Непосредственно из определения следует, что функции
Функции бывают возрастающие и убывающие.
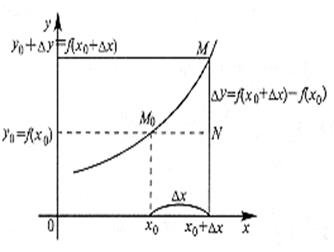
Определение: Функция называется возрастающей в интервале, если большему значению аргумента из этого интервала соответствует большее значение функции, то есть при ∆Х>0 приращение функции ∆У>0. Функция называется убывающей в интервале, если большему значению аргумента из этого интервала соответствует меньшее значение функции, то есть при ∆Х>0 приращение функции ∆У<0.
Некоторые свойства графиков функций.
Рассмотрим основные принципы построения графиков функции вида:
Если к аргументу функции прибавляется (вычитается) произвольное положительное число С, то происходит смещение графика функции вдоль оси абсцисс на С единиц влево (вправо) по отношению к исходному графику. Если аргумент функции умножается (делится) на постоянное положительное число А (А>1), то график этой функции сжимается (растягивается) по оси абсцисс в А раз по сравнению с исходным графиком. Если аргумент функции умножается (делится) на постоянное отрицательное число А, большее единицы, то график этой функции сжимается (растягивается) по оси абсцисс в А раз по сравнению с исходным графиком и зеркально отображается относительно оси ординат. Если к функции прибавляется (отнимается) какое-либо положительное число А, то график этой функции перемещается по оси ординат на А единиц вверх (вниз). Если функция умножается на произвольное число А, большее единицы, то график этой функции вытягивается по оси ординат в А раз, если число А положительно, и кроме этого зеркально отображается относительно оси абсцисс, если число А отрицательно.
Решение: Построим сначала график функции
Пример 2. Построить графики функции: Решение: Построим сначала график функции Предел функции.
Функции могут иметь предел. Что же нужно понимать под пределом функции?
Для первого графика, изображенного на рисунке,
Можно дать более строгое определение предела функции: пусть функция Математическая запись предела функции:
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 854; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 , где a – действительное число.
, где a – действительное число. , где а – положительное число не равное единице.
, где а – положительное число не равное единице. , где а – основание логарифма – положительное число, не равное единице.
, где а – основание логарифма – положительное число, не равное единице. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. .
.





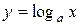 ; а >0 и а ≠1.
; а >0 и а ≠1.


 , (k=0; ±1; ±2…). Функция
, (k=0; ±1; ±2…). Функция  также определена везде, кроме точек
также определена везде, кроме точек  , (k=0; ±1; ±2…).
, (k=0; ±1; ±2…). , называется периодической, если существует такое постоянное число Т, при прибавлении или вычитании которого от аргумента значение функции не изменятся, т.е.
, называется периодической, если существует такое постоянное число Т, при прибавлении или вычитании которого от аргумента значение функции не изменятся, т.е. ,
,  .
. . Функции
. Функции  имеют период
имеют период  .
.

 .
.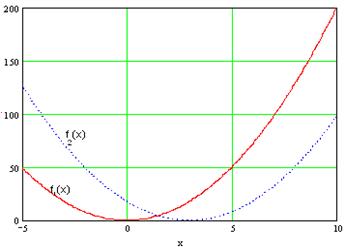 Пример 1. Построить графики функции:
Пример 1. Построить графики функции:  .
. , а затем сместим его по оси абсцисс на три единицы вправо и получим график функции
, а затем сместим его по оси абсцисс на три единицы вправо и получим график функции 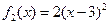 .
.
 .
. Определение: Функция у=f(x) имеет предел А при х→а, если при приближении х к а значение функции как угодно близко подходит к А, то есть
Определение: Функция у=f(x) имеет предел А при х→а, если при приближении х к а значение функции как угодно близко подходит к А, то есть  .
. , а для второго
, а для второго  .
. .
.


