
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 5. Неопределенный интеграл.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Первообразная. Неопределенный интеграл. Определение: Функция F(x), дифференцируемая на интервале (a, b), называется первообразной для функции f (x) на данном интервале, если для всех значений х, принадлежащих этому интервалу, выполняется равенство: Например: Если для некоторой функции существует хотя бы одна первообразная, то можно утверждать, что для нее существует бесчисленное множество первообразных, различающихся между собой на постоянные величины. Определение: Совокупность всех первообразных функций F(x)+C для функции f(x) называется неопределенным интегралом этой функции и обозначается
При этом f(x) называют подынтегральной функцией. А выражение f(x)dx – подынтегральным выражением.
Процесс нахождения первообразной функции называется интегрированием, причем аргумент х подынтегральной функции выступает здесь также в качестве переменной интегрирования. Интегрирование – действие, обратное дифференцированию, его можно проверить дифференцированием, причем дифференцирование однозначно, а интегрирование дает ответ с точностью до постоянной.
Всегда ли существует первообразная для заданной функции f(x)? Примем без доказательства, что если функция непрерывна на (a, b), то она имеет первообразную, а, следовательно, и неопределенный интеграл на этом интервале.
Геометрический смысл неопределенного интеграла.
Геометрический смысл неопределенного интеграла – это семейство графиков первообразных
Пример: Известно, что график функции f(x) проходит через точку А(2,5), а скорость изменения данной функции имеет вид
Решение:
Чтобы научиться находить первообразную функции, в первую очередь необходимо выучить наизусть таблицу неопределенных интегралов от основных элементарных функций. Она получается в результате обращения соответствующих формул дифференцирования. Например, если Таблица основных интегралов
Свойства неопределенного интеграла
Рассмотрим простейшие свойства неопределенного интеграла, которые позволят интегрировать не только основные элементарные функции.
1) Производная от неопределенного интеграла функции f(x) равна самой этой функции:
2) Дифференциал от неопределенного интеграла равен подынтегральному выражению:
3) Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до константы:
Пример: ∫dx=х+с. Пример: 4) Постоянный множитель можно выносить за знак интеграла:
Пример: 5) Интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов этих функций, т.е.
Пример:
Формула интегрирования остается справедливой, если переменная интегрирования является функцией: если Пример:
В интегральном исчислении нет универсального способа интегрирования. Применение различных методов приводит данный интеграл к табличному, который надо узнать с учетом свойства инвариантности.
Методы интегрирования 1) Непосредственное интегрирование. Этот метод заключается в прямом использовании табличных интегралов и их свойств. Пример: Пример: Пример: Следует отметить, что хотя при взятии каждого интеграла появляется своя константа, однако окончательный результат выражается через одну произвольную постоянную, являющуюся их линейной комбинацией. 2) Метод разложения Этот метод заключается в разложении подынтегральной функции в линейную комбинацию более простых функций с использованием известных формул.
Пример: Пример:
Пример;
3) Метод подведения под знак дифференциала. В данном методе для приведения искомого интеграла к табличному виду преобразовывают дифференциал аргумента функции. Дифференциал не меняется, если к переменной прибавить или отнять постоянную величину, а если переменную увеличить в несколько раз, то дифференциал необходимо умножить на обратную величину, то есть Пример: Пример: Пример:
4) Метод выделения полного квадрата из квадратичного трехчлена. Пример: Пример: 5) Метод замены переменных Этот метод основан на замене переменной интегрирования в неопределенном интеграле. Основная цель - свести его нахождение к нахождению такого определенного интеграла, который может быть найден методом разложения. Замечание. Подведение под знак дифференциала является частным случаем замены переменной, так как выполняются те же действия, только не вводится новая переменная. Пример: ∫ Введем новую переменную z=x+2. Найдем из этого уравнения связь между дифференциалами старой и новой переменной. Для этого продифференцируем левую и правую часть уравнения z=x+2. Получим: dz=dx. Тогда наш интеграл примет вид:
Пример: Если внимательно посмотреть на числитель и знаменатель подынтегрального выражения, то можно заметить, что числитель с точностью до постоянного множителя представляет собой дифференциал знаменателя. Тогда можно ввести новую переменную z=x
Перейдя к старой переменной в конечном результате, получим искомое решение интеграла. Пример: Введем замену переменной: Подставим замену в исходное выражение и возьмем интеграл:
Пример: Введем замену переменной: Продифференцируем данное выражение: Выразим dx через dz. Получим: Подставим замену в исходное выражение и возьмем интеграл:
Пример: Введем замену u=cosx. Продифференцируем данное выражение: du= -sinx∙dx. Выразим du через dx, подставим в исходное выражение и возьмем интеграл:
Пример: Используем подстановку u=sinx и du=cosx∙dx. Тогда
6) Интегрирование по частям. Этот метод основан на использовании формулы интегрирования по частям:
1) Интегралы вида Р(х)- многочлен решаются по частям при замене dv=P(x)dx, и u – другие сомножители. Пример: Подынтегральное выражение подставим виде udv. Через u следует обозначить lnx, а через dv=xdx. Тогда du= Пример: Обозначим u=arcsinx, тогда Пусть dv=dx, тогда Искомый интеграл будет равен: Интеграл в правой части можно взять методом подстановки. Введем подстановку: 1-x
Теперь подставим полученную формулу в первоначальный интеграл:
2) Интегралы вида Р(х) –многочлен, к – константа решаются по частям, при обозначении u=P(X), а dv – все остальные сомножители. Пример: Пример:
3) Интегралы вида Здесь надо сначала сделать замену переменной, а затем интегрировать по частям. Пример:
4) Интегралы вида Пример: Обозначим u=e Обозначим dv=cosxdx, тогда v= Применим формулу интегрирования по частям:
Возьмем еще раз правый интеграл Тогда Подставим значение полученного интеграла в выражение исходного интеграла, получим: Перенесем последний интеграл правой части в левую сторону уравнения и получим:
Следует отметить, что, несмотря на то, что последний способ интегрирования представляется наиболее сложным из рассмотренных, универсальным он не является, и его следует использовать лишь в тех случаях, когда предыдущие способы не дают необходимого результата.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 2897; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.37.236 (0.013 с.) |

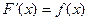 .
. является первообразной для
является первообразной для  , так как
, так как  , но
, но  , тоже первообразная функции
, тоже первообразная функции 
 есть первообразные функции
есть первообразные функции 

 , смещенных вдоль оси OY на произвольную константу. На рисунке представлен пример первообразных для функции у= -cosх.
, смещенных вдоль оси OY на произвольную константу. На рисунке представлен пример первообразных для функции у= -cosх.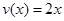 . Построить график функции f(x).
. Построить график функции f(x). Так как функция f(x) является первообразной для функции v(x), то значение ее можно найти, взяв неопределенный интеграл от функции v(x).
Так как функция f(x) является первообразной для функции v(x), то значение ее можно найти, взяв неопределенный интеграл от функции v(x).  . Ответ получен с точностью до константы С, найти которую можно из дополнительного условия: график функции f(x) должен проходить через точку А(2,5). Подставим в выражение функции f(x) координаты точки А и получим:
. Ответ получен с точностью до константы С, найти которую можно из дополнительного условия: график функции f(x) должен проходить через точку А(2,5). Подставим в выражение функции f(x) координаты точки А и получим:  . Тогда искомая функция будет иметь вид:
. Тогда искомая функция будет иметь вид:  - это парабола.
- это парабола. , то
, то  . Далее необходимо знать свойства неопределенного интеграла и освоить простейшие приемы интегрирования.
. Далее необходимо знать свойства неопределенного интеграла и освоить простейшие приемы интегрирования.









 .
. .
. .
.
 .
.

 .
. , то
, то  , где
, где  - произвольная функция, имеющая непрерывную производную. Это свойство называется инвариантностью.
- произвольная функция, имеющая непрерывную производную. Это свойство называется инвариантностью. ,
,  . Сравните с
. Сравните с 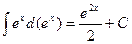 .
.
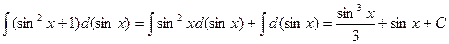




 .
.

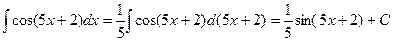


 .
. .
. =
=  =ln│z│+c= ln│x+2│+c
=ln│z│+c= ln│x+2│+c .
. +7. Тогда связь между dz и dx можно найти из последнего выражения, продифференцировав левую и правую его части: dz=2x∙dx. Тогда наш интеграл примет вид табличного интеграла:
+7. Тогда связь между dz и dx можно найти из последнего выражения, продифференцировав левую и правую его части: dz=2x∙dx. Тогда наш интеграл примет вид табличного интеграла: =
= 

 , так, чтобы избавиться от квадратного корня в знаменателе. Тогда
, так, чтобы избавиться от квадратного корня в знаменателе. Тогда  . Затем продифференцируем данное выражение:
. Затем продифференцируем данное выражение:  . Значит,
. Значит,  .
.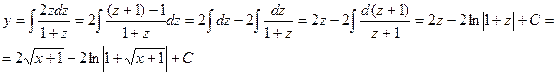

 .
. .
. .
.
 .
. = -
= -  = -ln│u│+c= - ln│cosx│+c
= -ln│u│+c= - ln│cosx│+c .
. =
=  =
= 
 , где u(x) и v(x) – функции, имеющие непрерывные производные в некотором промежутке. При использовании данной формулы нахождение исходного интеграла
, где u(x) и v(x) – функции, имеющие непрерывные производные в некотором промежутке. При использовании данной формулы нахождение исходного интеграла  сводится к нахождению интеграла
сводится к нахождению интеграла 
 , причем эту процедуру имеет смысл проводить лишь в том случае, если новый интеграл проще исходного и может быть найден с использованием рассмотренных выше способов интегрирования.
, причем эту процедуру имеет смысл проводить лишь в том случае, если новый интеграл проще исходного и может быть найден с использованием рассмотренных выше способов интегрирования. ,
,  ,
,  , где
, где
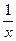 dx, а v=
dx, а v=  . Согласно формуле интегрирования по частям:
. Согласно формуле интегрирования по частям: 
 .
. .
. .
.

 .
. ,
,  ,
,  , где
, где , где обозначили: x=u, тогда
, где обозначили: x=u, тогда  , а sin(х)dx=dv, тогда
, а sin(х)dx=dv, тогда  .
. , где обозначили u=x, тогда
, где обозначили u=x, тогда  , тогда
, тогда  .
. ,
,  .
. , где сделали сначала замену переменной x=t², тогда dx=2tdt, а затем взяли интеграл по частям по аналогии с предыдущим примером.
, где сделали сначала замену переменной x=t², тогда dx=2tdt, а затем взяли интеграл по частям по аналогии с предыдущим примером. ,
,  , где a и b – константы берутся следующим образом: за u можно взять
, где a и b – константы берутся следующим образом: за u можно взять  , sin(bx) или cos(bx). Замена производится дважды.
, sin(bx) или cos(bx). Замена производится дважды.
 , тогда du=e
, тогда du=e  =sinx.
=sinx. -
-  .
. = -cosx.
= -cosx.


 , тогда
, тогда 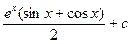 .
.


