
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типы неопределенных выраженийСодержание книги Поиск на нашем сайте
При решении различных практических задач большую роль играют так называемые неопределенные выражения или, коротко, неопределенности. Рассмотрим основные их типы. Пусть имеются две функции u(x) и v(x). 1. Пусть 2. Пусть 3. Пусть Степенные неопределенности. Рассмотрим теперь предел вида Так как
Это можно сформулировать в виде следующего правила: для вычисления предела выражения вида u(x)v(x) надо это выражение сначала прологарифмировать. Какие же неопределенности могут иметь здесь место? Так как приходится вычислять lim[u(x)v(x)], а здесь возможна только неопределенность типа 4. 5. 6.
9) Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы. Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля. Ранг матрицы — Размерность образа dim (im (A)) линейного оператора, которому соответствует матрица. Обычно ранг матрицы A обозначается иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков. Определение Пусть Тогда по определению рангом матрицы A является:ноль, если A — нулевая матрица;
число ему минор порядка (r + 1), если они существуют.
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 244; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.187.121 (0.009 с.) |

 . Тогда предел вида
. Тогда предел вида 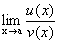 называется неопределенностью типа
называется неопределенностью типа  . Процесс вычисления этого предела называется "раскрытием неопределенности". Разумеется, что формула
. Процесс вычисления этого предела называется "раскрытием неопределенности". Разумеется, что формула 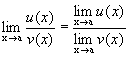 здесь неприменима. так как
здесь неприменима. так как 
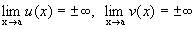 . Тогда предел вида
. Тогда предел вида  .
.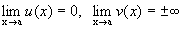 . Тогда предел вида
. Тогда предел вида 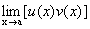 называется неопределенностью типа
называется неопределенностью типа 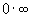 . Разумеется, и здесь нельзя пользоваться формулой
. Разумеется, и здесь нельзя пользоваться формулой 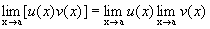
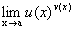 .
.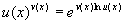 , то, пользуясь непрерывностью функции ex, можно записать
, то, пользуясь непрерывностью функции ex, можно записать .
.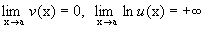 . Последнее означает, что
. Последнее означает, что 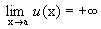 и поэтому говорят, что мы имеем дело с неопределенностью типа
и поэтому говорят, что мы имеем дело с неопределенностью типа  .
.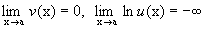 . Последнее означает, что
. Последнее означает, что  и поэтому говорят, что мы имеем дело с неопределенностью типа 00.
и поэтому говорят, что мы имеем дело с неопределенностью типа 00. . Последнее означает, что
. Последнее означает, что  и поэтому говорят, что мы имеем дело с неопределенностью типа 1¥.
и поэтому говорят, что мы имеем дело с неопределенностью типа 1¥.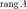 (
( ) или
) или 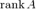 . Оба обозначения пришли к нам из
. Оба обозначения пришли к нам из — прямоугольная матрица.
— прямоугольная матрица. , где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к н
, где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к н порядка k равны нулю (Mk = 0).
Тогда
порядка k равны нулю (Mk = 0).
Тогда 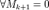 , если они существуют. Связанные определения Базисный минор
, если они существуют. Связанные определения Базисный минор
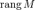 матрицы M размера
матрицы M размера 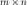 называют полным, если
называют полным, если  .
.
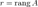 . Строки и столбцы, на
. Строки и столбцы, на
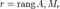 — базисный минор матрицы A, тогда: базисные строки и базисные столбцы линейно независимы;
— базисный минор матрицы A, тогда: базисные строки и базисные столбцы линейно независимы;
 , то строки и столбцы этой матрицы линейно зависимы. Пусть
, то строки и столбцы этой матрицы линейно зависимы. Пусть  , тогда максимальное количество
, тогда максимальное количество
 над полем C (или R). Пусть T — линейное преобр
азование, соответствующее A в стандартном базисе; это значит, что T (x) = Ax. Ранг матрицы A — это размерность области
значений преобразования T.
над полем C (или R). Пусть T — линейное преобр
азование, соответствующее A в стандартном базисе; это значит, что T (x) = Ax. Ранг матрицы A — это размерность области
значений преобразования T.



