
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоремы о пределах функций.Содержание книги
Поиск на нашем сайте 1). Предел постоянной величины равен этой величине:
2). Предел суммы (разности) конечного числа функций равен соответствующей сумме (разности) пределов этих функций:
3). Предел произведения конечного числа функций равен произведению пределов этих функций:
4). Предел частного двух функций равен частному пределов этих функций при условии, что делитель не будет равен нулю:
Некоторые важные пределы. 1). 2). 3). Вычисление пределов. Для вычисления пределов используют основные теоремы и правило Лопиталя (при возникновении «неопределенности» вида 0/0 или ∞∕∞), согласно которому предел частного двух функций равен пределу отношений производных этих функций: Пример 1. Найти предел функции: Решение: Пример 2. Найти предел функции: Решение:
Пример 3. Найти предел функции: Решение:
Пример 4. Найти предел функции: Решение: Пример 5. Найти предел функции: Решение:
Пример 6. Найти предел функции: Решение: При подстановке х=0 получаем неопределенность 0/0. Тогда по правилу Лопиталя: Пример 7. Найти предел функции: Решение: При подстановке х=2 получаем неопределенность 0/0, которую раскрываем по правилу Лопиталя:
Пример 8. Найти предел функции: Решение: При подстановке х=∞ получаем неопределенность ∞∕∞, которую раскрываем по правилу Лопиталя:
Непрерывность функции.
Большинство функций, изучаемых в математическом анализе, являются непрерывными, то есть при небольших изменениях аргумента х функция у меняется также мало, и график такой функции является непрерывной кривой. Однако, у некоторых функций при определенных значениях х непрерывность может нарушаться и график прерываться, тогда говорят, что функция в данных точках имеет разрыв. Значения аргумента, при которых происходит разрыв функции, называются точками разрыва. Определение: Функция y=f(x) непрерывна в точке x0, если в этой точке у нее существует предел Определение: Функция у=f(x) называется непрерывной в интервале, если она непрерывна в каждой точке этого интервала.
Отметим, что, вычисляя предел функции f(х), мы можем приближать х к x0 как справа, так и слева, то есть вычислять Непрерывность функции в точке x0 равносильна ее непрерывности в этой точке одновременно слева и справа, то есть должны выполняться следующие четыре условия непрерывности: 1). Функция должна быть определена в некоторой окрестности точки x0. 2). Должны существовать конечные пределы слева и справа:
3). Эти пределы должны быть равны между собой и равны А:
4). Эти пределы должны быть равны значению функции в точке x0, то есть А=f(x0).
Если в точке x0 не выполняется хотя бы одно условие, то в этой точке функция терпит разрыв, а сама эта точка называется точкой разрыва. Если выполняются условия 1 и 2, но нарушены условия 3 и 4, то точку x0 называют точкой разрыва первого рода. Если хотя бы один из пределов слева или справа бесконечен или его вовсе нет, тогда говорят о разрыве второго рода. Пример: тригонометрические функции sinx и cosx непрерывны повсюду, функция tg(x) имеет разрыв второго рода в точках Раздел 2. Производная функции.
Понятие производной.
Определение: Пусть имеется функция
Следует заметить, что у некоторых функций может не существовать предел отношения приращения функции к приращению аргумента в каких-то точках, то есть в этих точках такие функции производной не имеют.
Функция, имеющая конечную производную в данной точке, называется дифференцируемой в этой точке. Очевидно, что необходимым условием дифференцируемости функции является ее непрерывность. Производная любой функции может быть найдена по формуле (*). Например:
Однако, так находить производную функции слишком долго, поэтому была разработана таблица производных основных элементарных функций, которой обычно и пользуются. Таблица производных элементарных функций, свойства производных.
Нахождение производной сложной функции. В этом случае необходимо применять следующие правила, получившие название «свойства производных»: 1. Производная алгебраической суммы дифференцируемых функций равна алгебраической сумме производных этих функций: если 2. Постоянный множитель можно выносить за знак производной: если 3. Производная произведения двух функций равна сумме произведений производной первой функции на вторую и производной второй функции на первую. Если заданы функции 4. Производная частного двух функций равна дроби, числитель которой равен разности произведений производной числителя на знаменатель и производной знаменателя на числитель, а знаменатель равен квадрату знаменателя исходной дроби. Пусть функция если 5. Производная сложной функции. Если функция u =j (x) имеет производную в точке x o, а функция y=f (u) имеет производную в соответствующей точке u о = j (x o), то сложная функция f [ j (x)] имеет производную в точке x o и справедлива следующая формула:
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1633; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 .
.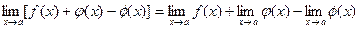 .
. 
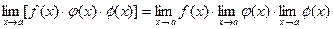 .
. , если только
, если только 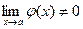 .
.
 , если х – длина дуги или угол, выраженный в радианах.
, если х – длина дуги или угол, выраженный в радианах.
 , при условии, что этот предел существует. Если после использования этого правила снова возникает неопределенность, то его применяют вторично.
, при условии, что этот предел существует. Если после использования этого правила снова возникает неопределенность, то его применяют вторично. .
. .
. .
. .
. .
.
 .
. .
. .
.
 .
. .
. .
. .
. .
. .
. .
. и
и  .
. ,
,  .
. =
=  = А.
= А. , где k=0; ±1; ±2…., а функция ctg(x) имеет разрыв второго рода в точках
, где k=0; ±1; ±2…., а функция ctg(x) имеет разрыв второго рода в точках  , где k=0; ±1; ±2….
, где k=0; ±1; ±2…. . Тогда, производной функции у по переменной х называется предел отношения приращения этой функции к приращению аргумента при стремлении последнего к нулю:
. Тогда, производной функции у по переменной х называется предел отношения приращения этой функции к приращению аргумента при стремлении последнего к нулю: (*).
(*). . Тогда:
. Тогда:









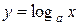







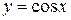













 , то
, то  .
. , то
, то  .
. и
и  , то
, то  .
. представляет собой отношение двух дифференцируемых функций
представляет собой отношение двух дифференцируемых функций  , то
, то 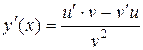 .
. . Таким образом, при нахождении производной сложной функции необходимо ввести промежуточный аргумент u= j (x), позволяющий свести данную функцию к виду основных элементарных функций f [ j (x)]=f(u), взять производную этой функции (в соответствии с таблицей производных), а затем умножить ее на производную от промежуточного аргумента.
. Таким образом, при нахождении производной сложной функции необходимо ввести промежуточный аргумент u= j (x), позволяющий свести данную функцию к виду основных элементарных функций f [ j (x)]=f(u), взять производную этой функции (в соответствии с таблицей производных), а затем умножить ее на производную от промежуточного аргумента.


