
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функциональный ряд. Ряд Тейлора.Содержание книги
Поиск на нашем сайте
Функциональный ряд - это ряд, слагаемыми которого являются функции. Из функциональных рядов чаще всего используют степенные ряды (это ряды, слагаемыми в которых являются степенные функции) и тригонометрические ряды (это ряды, слагаемыми в которых являются функции sin и cos).
Рассмотрим степенной ряд вида: Данный ряд будет сходиться, если
Рассмотрим свойства степенного ряда:
1) Сумма степенного ряда есть функция непрерывная в интервале сходимости ряда 2) Степенной ряд можно почленно интегрировать в интервале сходимости. 3) Степенной ряд можно почленно дифференцировать в интервале его сходимости (причем любое число раз).
Т.О. Сумма степенного ряда в интервале сходимости этого ряда является непрерывной и бесконечное число раз дифференцируемой функцией.
Возникает вопрос: если у нас есть функция f(x) – непрерывная и бесконечное число раз дифференцируемая, то можно ли ее представить в виде степенного ряда? И как при этом найти коэффициенты данного ряда? Возьмем непрерывную и бесконечное число раз дифференцируемую функцию f(x) и представим ее в виде степенного ряда: при при при при
Тогда любой коэффициент данного ряда можно найти по формуле:
Делаем вывод: любую непрерывную и бесконечное число раз дифференцируемую функцию можно разложить в степенной ряд, который получил название ряда Тейлора и имеет вид: (*) Определение: Рядом Тейлора функции f(x) в окрестности точки x0 называется степенной ряд (*) относительно разности (x-x0), коэффициенты которого
Но чаще всего на практике используется не ряд Тейлора, а ряд Маклорена, который является частным случаем ряда Тейлора. Ряд Маклорена – это разложение функции f(x) в ряд Тейлора в окрестности точки x0= 0, тогда он примет вид:
Чтобы замена функции f(x) на ряд Тейлора была правомочна, необходимо, чтобы ряд сходился к нашей функции f(x). Когда же ряд Тейлора сходится к f(x) -? Условие сходимости ряда Тейлора к f(x). Теорема. Если в некотором интервале, окружающем точку x0, абсолютные величины всех производных функции f(x) ограничены одним и тем же числом, то ряд Тейлора в этом интервале сходится к функции f(x).
Т.О. Разложение заданной функции в ряд Тейлора в окрестности точки x0 распадается на два этапа: 1) сначала находят производные функции f(x) в точке x0 и составляют ряд Тейлора; 2) находят интервал, в котором ряд Тейлора сходится к функции f(x).
Применение ряда Тейлора:
1) для приближенных вычислений значений функции; 2) для интегрирования сложных функций; 3) для решения дифференциальных уравнений.
Пример 1. Разложить функцию
Решение. Ряд Маклорена имеет вид
Найдем коэффициенты этого ряда:
.....
Подставив коэффициенты в ряд Маклорена, получим:
Найдем интервал, в котором полученный ряд сходится к функции Так как
Пример 2. Найти приближенное значение функции е. Решение. В предыдущем примере было получено разложение функции Используем данное разложение, присвоив переменной х значение 1. Тогда получим: Пример 3. Разложить функцию
Решение. Ряд Маклорена имеет вид Найдем коэффициенты этого ряда:
Подставив коэффициенты в ряд Маклорена, получим разложение функции Найдем интервал, в котором полученный ряд сходится к функции Так как
Пример 4. Найти значение определенного интеграла
Решение: Возьмем данный интеграл путем разложения подынтегральной функции Sinx в ряд Маклорена.
Разделим каждое слагаемое на х и разложим данный интеграл на сумму интегралов, которые являются табличными. Найдем значение этих интегралов:
Пример 5. Разложить функцию Решение. Ряд Тейлора имеет вид
Подставив коэффициенты в ряд Тейлора, получим Область сходимости этого ряда можно найти по формуле Пример 6. Найти приближенное значение функции Решение: Для этого разложим в ряд Маклорена функцию Ряд Маклорена имеет вид
Тогда коэффициенты данного ряда будут равны:
Подставив их значение в ряд получим: Найдем значение логарифмической функции в точке 2
Ряд Фурье и интеграл Фурье Если любую непрерывную в окрестности точки x0 и бесконечное число раз дифференцируемую функцию можно разложить в ряд Тейлора в окрестности точки x0, то любую периодическую функцию f(x), заданную в интервале
Разложение функции в ряд Фурье называют гармоническим анализом, а
Необходимо разложить в ряд Фурье периодическую функцию у=х заданную на интервале 0<χ<2π (см. рисунок). Запишем общий вид ряда Фурье и найдем его коэффициенты.
Аналогично
Результатом гармонического анализа является построение амплитудного спектра сложной функции. Амплитудный спектр функции – это график зависимости амплитуды гармоник, составляющих данную функцию от их частоты.
Построим амплитудный спектр периодической функции f(x), которая раскладывается в следующий ряд Фурье: График этой функции представлен на рисунке. Амплитудный спектр данной функции
Следует отметить, что амплитудный спектр периодической функции всегда дискретный.
Гармонический анализ широко применяется при исследовании сложных функциональных кривых, получаемых в электрокардиографии, электроэнцефалографии и т.п.
Как анализировать непериодическую функцию?.
Знак интеграла показывает, что суммируются гармоники с плавно меняющейся амплитудой, поэтому амплитудный спектр непериодической функции всегда непрерывный. Следует отметить, что любую непериодическую и интегрируемую на интервале
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 639; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.78.185 (0.007 с.) |

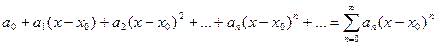 , где
, где  - являются коэффициентами степенного ряда.
- являются коэффициентами степенного ряда. , то есть для значений х, находящихся вблизи
, то есть для значений х, находящихся вблизи  , или
, или 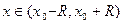 , где R – называется радиусом сходимости ряда. Радиус сходимости может быть определен по формуле
, где R – называется радиусом сходимости ряда. Радиус сходимости может быть определен по формуле  . Для других значений х ряд может расходиться.
. Для других значений х ряд может расходиться. , где R – радиус сходимости ряда.
, где R – радиус сходимости ряда. Попробуем найти коэффициенты этого ряда:
Попробуем найти коэффициенты этого ряда: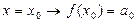 .
.




 .
.
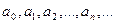 выражаются через функцию f(x) и ее производные в точке x0 по формулам:
выражаются через функцию f(x) и ее производные в точке x0 по формулам:
 .
. в ряд Маклорена и найти интервал сходимости этого ряда.
в ряд Маклорена и найти интервал сходимости этого ряда. .
.




 на всей числовой прямой, следовательно, ряд Маклорена сходится к
на всей числовой прямой, следовательно, ряд Маклорена сходится к 
 в ряд Маклорена и найти интервал сходимости этого ряда.
в ряд Маклорена и найти интервал сходимости этого ряда. .
.



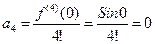
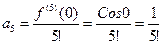
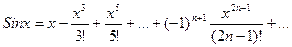
 на всей числовой прямой, следовательно, ряд Маклорена сходится к
на всей числовой прямой, следовательно, ряд Маклорена сходится к 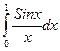 , который не берется обычными методами.
, который не берется обычными методами.


 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки  .
. . Найдем коэффициенты этого ряда:
. Найдем коэффициенты этого ряда:




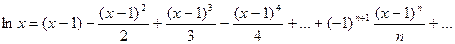
 , где R – радиус сходимости ряда. Данный ряд будет сходиться, если
, где R – радиус сходимости ряда. Данный ряд будет сходиться, если  .
.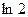 .
. .
. . Найдем производные этой функции:
. Найдем производные этой функции:

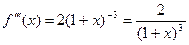
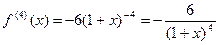
 ,
, ,
, ,
, ,
, , ….
, ….

 и имеющую интеграл в этом интервале можно представить в виде тригонометрического ряда или разложить в ряд Фурье:
и имеющую интеграл в этом интервале можно представить в виде тригонометрического ряда или разложить в ряд Фурье: , где
, где

 и
и  - гармониками функции f(x). Величины
- гармониками функции f(x). Величины  и
и  - амплитуды гармоник, а n- их частота.
- амплитуды гармоник, а n- их частота. Пример:
Пример: ,
, .
.
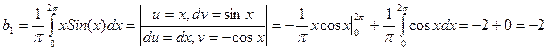 ,
, и т.п. Тогда
и т.п. Тогда  .
. Пример:
Пример: .
. будет иметь вид двух гармоник с частотами 1 и 2.
будет иметь вид двух гармоник с частотами 1 и 2. Фурье предложил рассматривать ее как периодическую на интервале
Фурье предложил рассматривать ее как периодическую на интервале  , тогда ряд Фурье превращается в интеграл Фурье:
, тогда ряд Фурье превращается в интеграл Фурье: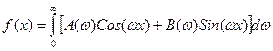 , где
, где

 A(w) и B(w) – амплитудные значения гармоник функции f(x), а w – их частота.
A(w) и B(w) – амплитудные значения гармоник функции f(x), а w – их частота.


