Учебное пособие по элементам высшей математики

для студентов высших медицинских учебных заведений

Челябинск, 2008 г.

УДК 510

 

 

Утверждено на заседании кафедры математики, информатики, биостатистики, доказательной медицины протокол № от и центральным методическим советом Чел.ГМА.

 

Н.В. Маркина, А.А. Болотов

 

Учебное пособие по элементам высшей математики для студентов высших медицинских учебных заведений.

 

 

Пособие написано в соответствии с программой по высшей математике и информатике для студентов первого курса медицинских высших учебных заведений.

Объем усл. печ. л.

 

Тираж 500 экз.

 

© ИМБДМ

 

 

Введение.

 

Настоящее пособие по основам высшей математики предназначено, в основном, для понимания курса биофизики в медицинских учебных заведениях. В курсе биофизики рассмотрение процессов в живых системах дается на уровне количественных закономерностей (электрогенез, биореология, биофизика клетки). Как правило, биофизические закономерности представляются в виде уравнений или функций. Для описания процессов используются дифференциальные уравнения. Таким образом, основным языком изложения материала биофизики является язык высшей математики и, в первую очередь, дифференциальное и интегральное исчисления.

С учетом, как правило, недостаточно высокого исходного уровня подготовки студентов по математике при изложении теоретической части материала основной упор сделан не на строгих математических доказательствах теорем и их свойств, а на их смысле и возможности практического применения.

Пособие содержит большое количество примеров и задач.

 

Раздел 1. Число. Переменная. Функция.

Действительные числа. Числовая последовательность.

Предел числовой последовательности.

Число – важнейшее математическое понятие. Возникшее в простейшем виде еще в первобытном обществе, понятие числа изменялось на протяжении веков, постепенно обогащаясь содержанием по мере расширения сферы человеческой деятельности. На первых ступенях развития понятие числа определялось потребностями счета. Так возникли натуральные числа (целые положительные числа, например: 1,2,5). Затем к натуральным числам присоединились дробные числа (например: 5,6; ¾), введение которых основывалось на необходимости производить измерения. Затем число становится основным понятием математики и дальнейшее его развитие определяется потребностями этой науки. Так развитие алгебры и геометрии привело к появлению отрицательных чисел. Числа целые, дробные (положительные и отрицательные) и нуль получили общее название рациональных чисел. Совокупности рациональных чисел оказалось недостаточно для изучения непрерывно изменяющихся переменных величин. Поэтому появилась необходимость в новом расширении понятия числа. К рациональным числам были добавлены иррациональные числа (это числа, которые могут быть представлены в виде бесконечной непериодической десятичной дроби, например: ). Совокупность рациональных и иррациональных чисел получила название действительных чисел.

Действительные числа, представленные в виде точек, непрерывно заполняют всю числовую ось.

Числовая ось – бесконечная прямая, на которой указана точка «О» - начало отсчета, положительное направление, отмеченное стрелкой, и масштаб для отображения чисел.

Бесконечное множество чисел , расположенных в определенном порядке одно за другим, называется числовой последовательностью.

Числа, входящие в последовательность, называются ее членами. Последовательность считается заданной, если известен закон ее образования, то есть правило, по которому можно определить любой член последовательности.

Если для данной последовательности существует число А, к которому числа при увеличении n подходят как угодно близко, то такое число А называется пределом последовательности . Например, для последовательности чисел 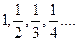пределом является А=0.