
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Величина. Область изменения величины.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
С помощью чисел мы можем количественно выражать различные свойства предметов и явлений. В этом случае число будет отражать значение рассматриваемой величины (например: масса тела равна 3 кг или скорость равномерного движения тела равна 5м/с). Величина – это понятие, которое позволяет выразить свойства предметов и явлений в количественном виде. Все величины можно разделить на переменные и постоянные. Постоянная величина - это такая величина, значения которой не меняются. Так например, при равномерном движении тела его скорость не изменяется. Однако бывают и абсолютно постоянные величины - величины, которые сохраняют своё значение в любом явлении. Например, число π – отношение длины окружности к её диаметру. Переменная величина – это такая величина, значение которой меняются в процессе ее наблюдения. Например, при равномерном движении меняется координата движущегося тела. При заболевании меняется температура тела человека.
Если величина меняется, то следует говорить об области ее изменения. Определение. Совокупность всех числовых значений переменной величины называется областью изменения этой величины. Область изменения переменной величины можно представить на числовой оси совокупностью точек, в простейшем случае отрезком числовой оси или интервалом. Интервал (или промежуток) – это совокупность всех чисел x числовой оси, заключенных между данными числами a и b, при этом числа a и b не принадлежат этой совокупности. Обозначение: a < x < b, или (a, b), или x Î (a, b). Символ Î обозначает слово «принадлежит». Если числа a и b принадлежат рассматриваемой совокупности, то область изменения называют отрезком (или сегментом, замкнутым промежутком, замкнутым интервалом). Обозначение: a ≤ x ≤ b или x Î [ a, b ]. Совершенно аналогично можно ввести понятие полузамкнутого интервала, когда одно из чисел a или b принадлежит рассматриваемой совокупности, а другое нет. Обозначение: a < x ≤ b или (a,b ]. Вполне понятно, что можно ввести и бесконечные интервалы (- ¥,¥). Упорядоченная переменная величина.
Обозначим произвольную переменную величину через x. Будем говорить, что переменная x есть упорядоченная переменная величина, если известна область изменения этой переменной величины, и про каждое из двух любых ее значений можно сказать, какое значение предыдущее и какое последующее.
Определение. Переменная величина называется возрастающей, если каждое ее последующее значение больше предыдущего. Переменная величина называется убывающей, если каждое ее последующее значение меньше предыдущего.
Функция.
При изучении различных явлений часто возникает задача изучения изменения одной величины в зависимости от изменения другой. Например, как меняется успеваемость студентов в зависимости от времени, потраченного на подготовку к занятиям. В этом случае мы приходим к понятию функции.
Определение. Совокупность значений x для которых правило вычисления значений y имеет смысл, называется областью определения функции или областью существования функции, а область изменения У называется множеством значений функции.
1.5. Способы задания функции.
1. Табличный способ задания функции. При этом способе выписываются в определенном порядке значения аргумента и соответствующие значения функции.
Примером таких таблиц могут служить таблицы тригонометрических функций, таблицы логарифмов, результаты экспериментов.
2. Графический способ задания функции. Если в прямоугольной системе координат на плоскости изобразить в виде линии некоторую совокупность точек так, что
Рис. 1.
Откладывая на оси абсцисс необходимое значение x и восстанавливая перпендикуляр из точки x до пересечения с кривой, а затем, проводя прямую, параллельную оси абсцисс до пересечения ее с осью ординат, получим значение функции 3. Аналитический способ задания функции. При аналитическом способе задания функция представляется аналитическим выражением, то есть через совокупность известных математических операций, которые производятся в определенной последовательности над числами и символами, обозначающими постоянные и переменные величины.
Примером аналитических выражений могут служить:
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.186.95 (0.008 с.) |

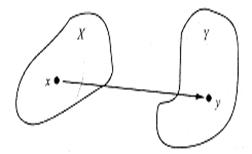 Определение. Если каждому значению одной переменной величины x, принадлежащему некоторой области изменения, по некоторому правилу можно поставить в соответствие одно или несколько значений другой переменной величины y, то говорят, что задана функция y от x:
Определение. Если каждому значению одной переменной величины x, принадлежащему некоторой области изменения, по некоторому правилу можно поставить в соответствие одно или несколько значений другой переменной величины y, то говорят, что задана функция y от x: 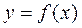 , где f есть некоторое правило, а х носит названиеаргумента функции.
, где f есть некоторое правило, а х носит названиеаргумента функции.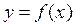 , где x – абсциссы точек, а y – ординаты, то такая совокупность точек называется графиком функции (рис. 1).
, где x – абсциссы точек, а y – ординаты, то такая совокупность точек называется графиком функции (рис. 1).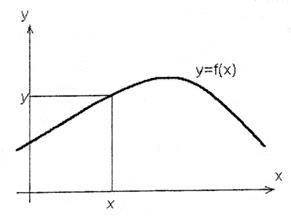
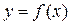 в точке x.
в точке x.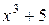 ,
, 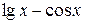 .
.


