
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 9. Введение в математические методы оптимизации.Содержание книги
Поиск на нашем сайте
Оптимизация производства.
Математические методы оптимизации (ММО) используются при решении задач, в которых требуется выбрать одно решение, оптимальное по какому-то критерию, из нескольких возможных. Пример 1. В районе обнаружены случаи опасного заболевания. Организуется медицинское обслуживание. Выделены средства, оборудование, медицинский персонал. Необходимо определить число медпунктов, их размещение, последовательность осмотров при условии ограничений на финансовые средства и ресурсы.
Пример 2. Необходимо приготовить раствор, содержащий вещество А и В. Даны два стандартных готовых раствора с концентрациями веществ в этих растворах Формализуем последний пример в следующем виде:
В общем случае можно записать так. Пусть даны только две переменные, система ограничений-неравенств и целевая функция:
Пример 3. Фирма производит два продукта А и В. Рынок сбыта неограничен. Для выпуска продукции А и В необходимо использовать два станка. Время операции (в часах) на каждом станке для выпуска изделий А и В приведено в таблице.
Время работы станков в неделю не может превышать 40 и 36 часов соответственно. Прибыль от продажи единицы продукции составляет 5 и 3 рубля соответственно. Необходимо определить, сколько каждого продукта необходимо выпускать, чтобы общая прибыль была максимальна. Формализуем данную задачу.
Рассмотрим геометрическую интерпретацию этой задачи. Пусть Первая прямая L1 получена из ограничения неравенства Тогда область ниже этих прямых будет соответствовать ограничениям-неравенствам
Перемещаем опорную линию Z параллельно самой себе в направлении, перпендикулярном опорной линии по допустимой области. Перемещение соответствует росту прибыли от нуля (начальное положение опорной линии с нулевой прибылью) до максимально возможной, что соответствует положению линии прибыли на границе допустимой области (линия Z1). Найдем координаты точки на плоскости, соответствующей максимальной прибыли. Координаты и будут равны оптимальному выпуску продукции.
В общем случае, если опорная линия параллельна одной из линий, полученной из ограничений-неравенств, а область допустимых решений лежит вне прямых, то решений бесчисленное множество, так как можно произвольно менять выпуск одной из продукции. Если область не замкнута, то оптимального решения нет. Эти ситуации показаны на рисунках, представленных ниже.
Если необходимо не максимизировать целевую функцию, а минимизировать, то опорная прямая идет не в сторону максимизации целевой функции, а в сторону минимизации (к началу координат) от произвольной точки внутри области допустимых решений. Если переменных больше двух, то графическое решение затруднительно и целесообразно искать его только на ЭВМ.
Транспортная задача. Пусть имеется три склада продукции и два потребителя. Например, есть три аптечных склада и две аптеки, получающих лекарства от трех складов. Лекарства доставляет транспортная компания, желающая минимизировать стоимость перевозок. Для простоты положим, что сумма всех запасов на складах в точности равна потребностям аптек. Это так называемая сбалансированная транспортная задача. Положим также, что обратных перевозок (от аптек на склад) нет. Обозначим Исходя из возможностей поставщиков:
Исходя из потребностей потребителей:
Это и есть формализованная транспортная задача. Ее оформление и решение обычно идет в серии таблиц, называемых транспортными. Рассмотрим ход решения на конкретном примере. Пусть поставщиков три, потребителей четыре. Задача сбалансированная. Исходные данные приведены в таблице. В ячейках таблицы приведены стоимости перевозок с соответствующего склада к конкретному поставщику. Обозначим поставщиков через А1, А2, А3. Потребителей – В1, В2, В3, В4.
Проверяем задачу на сбалансированность: 150+120+80+50=400, 100+130+170=400. Задача сбалансированная. Решение идет в несколько этапов. 1. Составляется первоначальный, так называемый, опорный план. Проще всего это сделать методом минимального элемента. Суть метода: из всей таблицы выбираем клетку с минимальной стоимостью перевозки. Это стоимость перевозки из склада А2 к потребителю В1. Стоимость 1 руб. Выделено жирным курсивом. Помещаем в эту клетку всю перевозку:
Далее из рассмотрения исключаем строку, если запас у этого поставщика израсходован, или столбец, если запрос удовлетворен. В нашем случае поставщик А2 перевезет весь свой запас в пункт В1 по стоимости за 1 руб. Однако, заявка В1 полностью не выполнена. Далее в последней таблице вновь ищем минимальную стоимость. Это С11=3 руб. Отправляем из А1 в В1 недостающие 20 единиц товара. Потребности В1 будут полностью удовлетворены. Промежуточная таблица примет вид:
Вновь ищем минимальный элемент. Это С12, поэтому всю перевозку направим из А1 в В2. Это будет 80 единиц. Вписываем это в таблицу.
Эту процедуру повторяем до тех пор, пока все запасы не будут развезены по потребителям. Получим итоговую таблицу, в которой содержится опорный план перевозок.
2. Второй этап: расчет полной стоимости перевозок и проверка плана на оптимальность (минимум стоимости). Полная стоимость перевозок:
Методов оптимизации существует достаточно много. Мы рассмотрим наиболее простой – метод псевдостоимостей или метод потенциалов. В этом методе вводят псевдостоимость в следующем виде: Эти условные стоимости могут быть как положительными, так и отрицательными и равными нулю. Стоимость перевозки здесь раскладывается на две части – стоимость вывоза и стоимость ввоза. Тогда становится понятно, что план будет только тогда оптимальным, если псевдостоимости будут меньше или равны реальным стоимостям перевозки. Тогда для тех клеток, в которых перевозки присутствуют, можно записать:
Составим систему уравнений для ненулевых клеток:
Найдем эти потенциалы для расчета псевдостоимостей и сравнения их с реальными стоимостями. Число уравнений меньше на единицу числа переменных. Поэтому любую переменную можно положить равной нулю. Чаще всего встречается
Вычисляем псевдостоимости и сравниваем их с реальными.
Так как есть псевдостоимости большие, чем стоимости, то предложенный опорный план не оптимален. Наибольшая разность, равная 2, в клетке (1,3). Следовательно, в план надо ввести перевозку из А1 в В3. В таблице опорного плана начинаем переставлять перевозки, начиная с этой клетки, не нарушая баланс задачи. Необходимо помнить, что перестановки перевозок должны идти только по замкнутому циклу, чтобы баланс задачи не нарушился.
Было:
Стало:
Рассчитываем стоимость перевозок.
Стоимость стала меньше. Вновь проверяем план на оптимальность.
Число уравнений 5, число переменных равно 5. Можно произвольно назначить значения двум переменным. Пусть
Вычисляем вновь псевдостоимости свободных клеток.
Вновь выбираем элемент с максимальной разностью стоимости и псевдостоимости и от него начинаем переставлять перевозки, контролируя, чтобы баланс задачи не нарушался.
Было:
Стало:
Определяем стоимость перевозок:
Проверяем на оптимальность. Определяем псевдостоимости и сравниваем их с реальными стоимостями:
Решение системы методом исключения и назначения произвольно значений свободным переменным дает:
Находим псевдостоимости:
Найденный план оптимален, так как все псевдостоимости меньше или равны реальным стоимостям. Минимальная стоимость перевозок равна 2040 руб.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 384; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.33.130 (0.008 с.) |

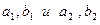 . Стоимость единицы раствора С1 и С2 соответственно. Надо, чтобы в растворе было вещества А не менее α, а В не менее β при условии минимальной стоимости.
. Стоимость единицы раствора С1 и С2 соответственно. Надо, чтобы в растворе было вещества А не менее α, а В не менее β при условии минимальной стоимости.


 оси Декартовой системы координат. Построим в этой системе координат прямые, полученные из ограничений-неравенств. В этой же системе координат построим прямую линию (Z), соответствующую целевой функции при нулевой начальной прибыли. Она называется опорной прямой.
оси Декартовой системы координат. Построим в этой системе координат прямые, полученные из ограничений-неравенств. В этой же системе координат построим прямую линию (Z), соответствующую целевой функции при нулевой начальной прибыли. Она называется опорной прямой. , прямая L2 – из
, прямая L2 – из  .
.




 количество продукции от склада i в аптеку j. Тогда можно записать две системы уравнений: исходя из возможностей поставщиков и исходя из потребностей аптек. Запишем эти системы.
количество продукции от склада i в аптеку j. Тогда можно записать две системы уравнений: исходя из возможностей поставщиков и исходя из потребностей аптек. Запишем эти системы.


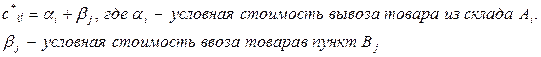
 .
.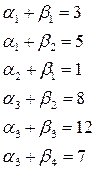

 . Пусть она будет равна нулю. Тогда решаем систему методом исключения неизвестных. Получим:
. Пусть она будет равна нулю. Тогда решаем систему методом исключения неизвестных. Получим: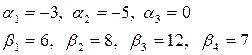

 805
805

 Отсюда,
Отсюда, 
 . Решаем систему уравнений обычным образом. В результате получим:
. Решаем систему уравнений обычным образом. В результате получим: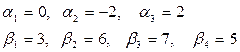

 20 3
20 3

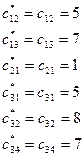 Отсюда,
Отсюда, 





