
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полный дифференциал функции.Содержание книги
Поиск на нашем сайте
Определение: Полным дифференциалом функции нескольких переменных называется сумма всех ее частных дифференциалов:
Пример 1: Найти полный дифференциал функции Решение: Поскольку частные производные этой функции равны:
То сразу можно записать частные дифференциалы этих функций:
Тогда полный дифференциал функции будет иметь вид:
Пример 2 Найти полный дифференциал функции Решение: Эта функция является сложной, т.е.
Находим частные производные:
Полный дифференциал:
Аналитический смысл полного дифференциала состоит в том, что полный дифференциал функции нескольких переменных представляет собой главную часть полного приращения этой функции, то есть имеет место приближенное равенство: ∆z≈dz. Необходимо, однако помнить, что эти приближенные равенства справедливы лишь при малых дифференциалах dx и dy аргументов функции z=f(x,y).
Применение полного дифференциала в приближенных вычислениях основано на использовании формулы ∆z≈dz. Действительно, если в данной формуле приращение ∆z функции представить в виде
откуда Полученную формулу можно использовать для приближенного нахождения «нового» значения функции двух переменных, которое она принимает при достаточно малых приращениях обоих ее аргументов.
Пример. Найти приближенное значение функции Решение. Подставив частные производные функции, найденные ранее в формулу, получим:
При подстановке значений х=1, ∆х=0,01, у=2, ∆у=0,02 получим:
Скалярное поле.
Если в каждой точке некоторой области пространства D задана функция U(p)=U(x,y,z), то говорят, что в области D задано скалярное поле. Если, например, U(x,y,z) обозначает температуру в точке М(х,у,z), то говорят, что задано скалярное поле температур. Если область D заполнена жидкостью или газом и U(x,y,z) обозначает давление, то имеется скалярное поле давлений. Если в пространстве задано расположение зарядов или массивных тел, то говорят о поле потенциала. Скалярное поле называется стационарным, если функция U(x,y,z) не меняется со временем: U(х,у,z) ≠ f (t).
Любое стационарное поле характеризуется: 1) поверхностью уровня скалярного поля 2) скоростью изменения поля в заданном направлении. Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция U(x,y,z) принимает постоянное значение, то есть U(x,y,z) = const. Совокупность этих точек образует некоторую поверхность. Если возьмем другую константу, то получим другую поверхность.
Направление наибольшего возрастания скалярной функции задается вектором, который называется градиентом и обозначается символом Градиент функции находится через частные производные этой функции и всегда перпендикулярен поверхности уровня скалярного поля в данной точке:
Производная от функции U(x,y,z) по любому другому направлению (λ) определяется по формуле:
α, β, γ – это углы между осями координат соответственно OX, OY, OZ и направлением Производную функции по направлению можно найти и через другую формулу:
Таким образом, производная функции по данному направлению равна скалярному произведению градиента функции на единичный вектор этого направления. В этом случае, производная по направлению вектора, касательного к поверхности уровня, равна нулю, а градиент в каждой точке перпендикулярен касательной плоскости к поверхности уровня, проходящего через данную точку. Пример на нахождение градиента функции в данной точке. Пусть дана функция Определим градиент в точке М(1,1,1). Выражение градиента этой функции в произвольной точке будет:
Следовательно,
|
|||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.238.22 (0.009 с.) |

 .
. .
.

 ,
,  ,
, .
.
 , где
, где 
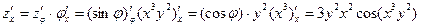


 , а полный дифференциал в виде
, а полный дифференциал в виде  , то получим:
, то получим: ≈
≈  ,
, .
. 1,01,
1,01,  .
. .
.
 Пример: Пусть задано скалярное поле
Пример: Пусть задано скалярное поле  . Примером такого поля является поле электрического потенциала точечного электрического заряда (+q). Здесь поверхностями уровня будут эквипотенциальные поверхности
. Примером такого поля является поле электрического потенциала точечного электрического заряда (+q). Здесь поверхностями уровня будут эквипотенциальные поверхности  , то есть сферы, в центре которых находится заряд, создающий поле.
, то есть сферы, в центре которых находится заряд, создающий поле. (или
(или  ).
). , где
, где

 - единичные векторы соответственно по осям OX, OY, OZ
- единичные векторы соответственно по осям OX, OY, OZ , где
, где .
.
 , где
, где  .
. .
. .
. ,
,  .
.


