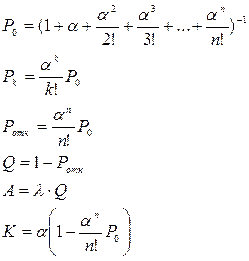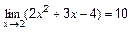Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Введение в теорию массового обслуживания. Формулы Эрланга.Содержание книги
Поиск на нашем сайте
Системы массового обслуживания (СМО) – это системы, предназначенные для обслуживания некоторого потока заявок, поступающих в какие-то случайные моменты времени. Примеры СМО: телефонная станция, аптека, парикмахерская, справочное бюро и т.п. СМО состоит из некоторого числа обслуживающих единиц, которые принято называть каналами обслуживания. В приведенных примерах под каналом обслуживания надо понимать телефонную линию, провизора, парикмахера, оператора справочной службы. Время обслуживания заявки также предполагается случайным. После обслуживания канал освобождается и готов к новому обслуживанию. Случайный характер потока заявок на обслуживание и случайное время обслуживания приводят к тому, что в какие-то моменты времени на входе СМО будет очередь, а в какие-то – простой. Предмет теории массового обслуживания: построение математических моделей, связывающих условия работы СМО с показателями эффективности работы СМО. Показатели эффективности работы СМО: 1. Среднее число заявок, обслуживаемых в единицу времени. 2. Среднее число занятых каналов. 3. Вероятность отказа в обслуживании. 4. Среднее время ожидания в очереди.
Составляющие СМО: 1. Входящий поток заявок. 2. Дисциплина очереди. 3. Механизм обслуживания. 4. Выходящий поток.
Схематически составляющие СМО показаны на рисунке.
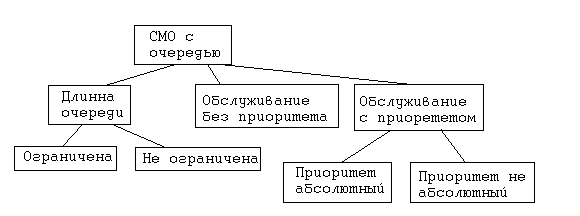
· СМО с отказами (как в телефонии, если номер занят, то соединение не происходит, говорят отказ в обслуживании). · СМО с очередью (магазин, касса, парикмахерская, автомойка).
СМО с очередью также подразделяются на следующие группы как показано на рисунке:
Рассмотрим более подробно входящий поток заявок, как одно из наиболее важных понятий. Потоком заявок на обслуживание называют совокупность заявок, поступающих на обслуживание. По регулярности появления заявок во времени потоки разделяют на регулярные и стохастические. При регулярном потоке заявки на обслуживание поступают строго через равные промежутки времени Важнейшая характеристика потока заявок – интенсивность потока. Под интенсивностью потока принято понимать среднее число требований на обслуживание за единицу времени. В случае регулярного потока интенсивность можно записать в виде:
Входящий не регулярный поток называют стационарным, если вероятность поступления определенного количества требований на обслуживание в течение определенного промежутка временизависит лишь от длины этого промежутка. В стационарном потоке Поток заявок называют без последействия, если для любых двух непересекающихся участков времени Пусть Если поток ординарен, стационарен и не имеет последействия, то его называют простейшим потоком заявок на обслуживание.
Для простейшего потока число заявок на обслуживание
Простейший поток еще называют стационарный пуассоновский поток заявок. Следующее важное понятие в СМО – время обслуживания
На примере классической задачи теории массового обслуживания, возникшей из практических нужд телефонии в начале 20 века, и впервые решенной датским математиком Эрлангом, рассмотрим основные показатели СМО и основные расчетные формулы для определения характеристик СМО. Эти формулы были названы формулами Эрланга. Они являются основным инструментом для определения технических характеристик СМО. Введем обозначения:
Необходимо найти: · А – абсолютную пропускную способность как среднее число заявок, обслуживаемых в единицу времени. · Q – относительную пропускную способность или среднюю долю пришедших заявок, обслуживаемых СМО. · Pотк – вероятность отказа в обслуживании. · K – Среднее число занятых каналов. · P0 – вероятность простоя СМО. · Pk – вероятность того, что занято ровно k каналов.
Введем еще одно обозначение для упрощения записи формул Эрланга:
Пример. Пусть имеется аптека, в которой пять продавцов. Пусть к ним обращаются покупатели с интенсивностью 1 человек в минуту. Время обслуживания одного покупателя есть случайная величина с показательным законом распределения и средним временем обслуживания 2 минуты. Предположим также, что покупатель уходит из аптеки не обслуженным, если все пять продавцов заняты в момент его прихода в аптеку. Необходимо вычислить основные характеристики СМО. Решение.
Таким образом,
Вывод: В аптеке в среднем заняты два продавца из пяти. Каждый продавец загружен только на 39%. Уходят не обслуженными каждые четыре человека из ста. Значит можно либо уволить несколько продавцов, либо увеличить интенсивность потока заявок. Раздел 10. Задачи по высшей математике для самостоятельной работы. Нахождение пределов функций
Проверить правильность нахождения пределов следующих функций:
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 3332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.215.149 (0.006 с.) |


 . При стохастическом потоке время появления заявки случайно.
. При стохастическом потоке время появления заявки случайно.
 .
.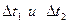 число заявок за время
число заявок за время  не зависит от того, сколько их было за время
не зависит от того, сколько их было за время  .
. - число заявок на обслуживание на интервале
- число заявок на обслуживание на интервале  . Тогда поток называют ординарным, если
. Тогда поток называют ординарным, если  , то есть в ординарном потоке за малый промежуток времени появление двух и более заявок на обслуживание практически невозможно.
, то есть в ординарном потоке за малый промежуток времени появление двух и более заявок на обслуживание практически невозможно.
 . Вполне понятно, что это случайная величина. Запомним без доказательства, что ее закон распределения имеет вид:
. Вполне понятно, что это случайная величина. Запомним без доказательства, что ее закон распределения имеет вид: , здесь
, здесь  Тогда
Тогда 

 - приведенная интенсивность потока заявок. Ее смысл – среднее число заявок, приходящееся на среднее время обслуживания одной заявки. С учетом принятых обозначений запишем основные формулы Эрланга.
- приведенная интенсивность потока заявок. Ее смысл – среднее число заявок, приходящееся на среднее время обслуживания одной заявки. С учетом принятых обозначений запишем основные формулы Эрланга.