
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема урока: «Неопределенный и определенный интеграл»
Группа: 1-ЭЛ-1 10.02.22 дисциплина: математика преподаватель: Левченко Н.Г.
План: 1. Изучить новый материал. 2. Сделать конспект. 3. Выписать примеры решения упражнений. 4. Выполнить задание.
1) Новый материал. Неопределенный интеграл функции y = f(x) – это совокупность всех первообразных функций F(x) + C для функции f(x). Обозначается Интегрирование–отыскание первообразной по ее производной. Это действие, обратное дифференцированию.
Основные свойства неопределенного интеграла: 1˚. (
2˚.
3˚.
4˚.
Основные формулы интегрирования (табличные интегралы): 1. ∫ dx = x + C, C – постоянная.
2.
3.
4. ∫ ex dx = ex + C. 5. ∫cosxdx = sin x + C. 6. ∫ sinxdx= - cosx + C. 7.
8.
9.
10.
11. Способ непосредственного интегрирования заключается в использовании основных свойств неопределенного интеграла и приведении подынтегрального выражения к табличному виду.
2). Примеры решения. 1.
2. = 4∙
3). Выполните задания:
Найти следующие интегралы: а) ∫ 3 dx; б) ∫ х11dx; в) ∫ 5х9dx; г) ∫ (4х3 – 6х2 – 4х + 3) dx; д) ∫ х -5dx; е) ∫ 43хdx; ж) ∫ е2хdx; з) ∫ 2cos(5x – 2) dx; и) ∫ (18х5 – 8х + 5) dx; к) ∫ (7sinx + 3) dx.
Определенный интегралот функции f(x), непрерывной на отрезке где то есть Формула называется формулой Ньютона – Лейбница. 4). Определенный интеграл. Основные свойства определенного интеграла: 1˚. 2˚. 3˚. 4˚. 5˚.
При вычислении определенного интеграла для нахождения первообразной используют те же методы, что и для нахождения неопределенного интеграла.
Пример: = (3x
5). Выполните задания:
а) г)
|
||||
|
Последнее изменение этой страницы: 2024-02-27; просмотров: 415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.103.14 (0.006 с.) |
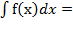 F(x) + C, где
F(x) + C, где  , f(x) − подынтегральная функция,
, f(x) − подынтегральная функция, 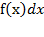 – подынтегральное выражение, С – постоянная интегрирования, способная принимать любое значение, х – переменная интегрирования.
– подынтегральное выражение, С – постоянная интегрирования, способная принимать любое значение, х – переменная интегрирования.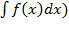 ′ = f(x)
′ = f(x) 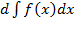 = f(x)dx
= f(x)dx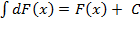
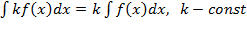
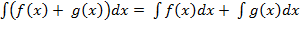 .
.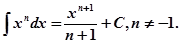
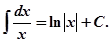
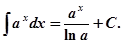
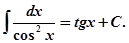
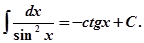
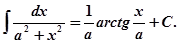
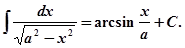

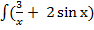 dx = 3
dx = 3 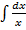 + 2
+ 2 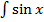 = 3
= 3 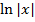 − 2
− 2 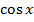 + C.
+ C.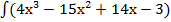 dx = 4
dx = 4 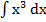 − 15
− 15 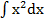 + 14
+ 14 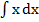 − 3
− 3 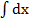 =
=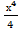 − 15∙
− 15∙ 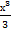 + 14 ∙
+ 14 ∙ 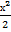 – 3х + C =
– 3х + C =  − 5
− 5 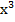 + 7
+ 7 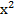 – 3х + С.
– 3х + С.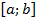 вычисляется по формуле:
вычисляется по формуле: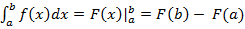 ,
,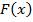 – первообразная для функции f(x),
– первообразная для функции f(x),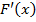 = f(x).
= f(x).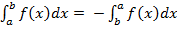 .
.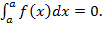
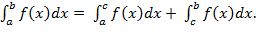
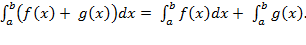
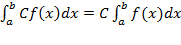 , C – const.
, C – const.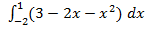 = (3x
= (3x 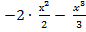 )|
)| 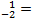
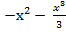 )|
)|  ) – (3·(−2) – (−2
) – (3·(−2) – (−2 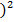 –
– 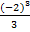 ) = 9.
) = 9.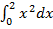 ; б)
; б) 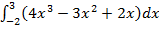 ; в)
; в) 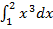 ;
; 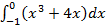 д)
д) 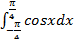 .
.


