
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4.2. Первообразная и определенный интеграл
Площадь криволинейной трапеции. Понятие об определенном интеграле. Первообразная. Первообразные элементарных функций. Правила вычисления первообразных. Формула Ньютона-Лейбница. Примеры применения интеграла в физике и геометрии.
Определение. Первообразной функцией
Теорема (теорема Коши). Любая непрерывная на некотором множестве функция имеет на этом множестве первообразную. Пример. Функция Каждая функция может иметь бесконечно много первообразных, которые отличаются на постоянное слагаемое. Верно и обратное утверждение. Теорема. Если Доказательство. Рассмотрим функцию
Определение. Совокупность всех первообразных данной непрерывной функции называется неопределенным интегралом от этой функции и обозначается Если Процесс нахождения неопределенного интеграла называется интегрированием данной функции, или взятием интеграла от данной функции. На основании теоремы 2
Функция имеет бесконечно много первообразных, которые отличаются друг от друга на постоянное слагаемое. Графики всех первообразных представляют собой бесконечное семейство параллельных кривых, которые заполняют всю плоскость. Через каждую точку плоскости проходит график одной из первообразных. Правила нахождения первообразных: 1. Постоянный коэффициент можно выносить за знак интегрирования: функции 2. Первообразная суммы функций равна сумме первообразных этих функций. Первообразные основных элементарных функций:
Определенный интеграл. Формула Ньютона-Лейбница.
Пусть функция
Где
Свойства определенного интеграла Ниже предполагается, что 1. 2. 3. 4. Если 5. 6. Если Формула Ньютона-Лейбница Пусть функция
Площадь криволинейной трапеции Площадь фигуры, ограниченной осью
Пусть
Замена переменной в определенном интеграле Определенный интеграл
Новые пределы интегрирования по переменной
Где Интегрирование по частям для определенного интеграла В этом случае формула интегрирования по частям имеет вид:
Пример. Вычислить интеграл
Решение. Применяя формулу Ньютона-Лейбница, получаем
Пример. Вычислить площадь фигуры, ограниченной линиями
Это типовая формулировка задания. Первый и важнейший момент решения – построение чертежа. Причем, чертеж необходимо построить правильно. При построении чертежа рекомендуется следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций. Графики функций выгоднее строить по точкам. В данной задаче решение может выглядеть так. Выполним чертеж (обратите внимание, что уравнение
На отрезке поэтому: Ответ: Пример. Вычислить площадь фигуры, ограниченной линиями
Решение: Выполним чертеж:
Если криволинейная трапеция полностью расположена под осью В данном случае:
В геометрии - вычисление площади фигуры под графиком. В физике - да там все через интеграл считается. Нахождение магнитного потока по напряженности, количества теплоты при известном токе и сопротивлении, магнитной индукции. Мощным средством исследования в математике, физике, механике и других дисциплинах является определенный интеграл – одно из основных понятий математического анализа. Геометрический смысл интеграла – площадь криволинейной трапеции. Физический смысл интеграла: 1) масса неоднородного стержня с плотностью; 2) перемещение точки, движущейся по прямой со скоростью за промежуток времени. Применение интеграла в физике: Работа
Вычисление массы. Вычисление момента инерции линии, круга, цилиндра. Вычисление координаты центра тяжести. Количество теплоты и т.д. Применение интеграла в геометрии: Вычисления Длина дуги кривой.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 772; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.102.239 (0.029 с.) |
 для функции
для функции  называется функция, производная которой равна исходной функции.
называется функция, производная которой равна исходной функции. .
. является первообразной функции
является первообразной функции  так как
так как  . Функции
. Функции  и
и  также являются первообразными функции
также являются первообразными функции  , где
, где  – произвольное число, является первообразной функции
– произвольное число, является первообразной функции  и
и  - две первообразные для функции
- две первообразные для функции  ,
,
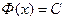 ,
, .
.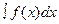 , где
, где  - подынтегральным выражением.
- подынтегральным выражением. , где
, где  – произвольная постоянная.
– произвольная постоянная. .
.
 .
.













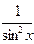

 . Определенный интеграл от функции
. Определенный интеграл от функции  вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю:
вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю: ,
,
 – непрерывные функции на замкнутом интервале
– непрерывные функции на замкнутом интервале  ;
; , где
, где  - константа;
- константа; ;
;
 для всех
для всех  то
то  ;
;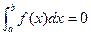 ;
; в интервале
в интервале  .
. .
. , двумя вертикальными прямыми
, двумя вертикальными прямыми  и графиком функции
и графиком функции  .
.

 – первообразные функций
– первообразные функций  на замкнутом интервале
на замкнутом интервале  и вертикальными линиями
и вертикальными линиями 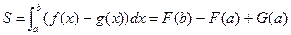 .
. по переменной
по переменной  можно преобразовать в определенный интеграл относительно переменной
можно преобразовать в определенный интеграл относительно переменной  с помощью подстановки
с помощью подстановки  :
:
 .
. - обратная функция к
- обратная функция к  , т.е.
, т.е.  .
. , где
, где  означает разность значений произведения функций
означает разность значений произведения функций  при
при 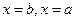 .
.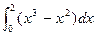
 .
. .
. задает ось
задает ось  ):
):
 график функции
график функции  расположен над осью
расположен над осью  .
. ед
ед  .
. и координатными осями.
и координатными осями.
 .
. .
.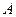 переменной силы.
переменной силы. – (путь) перемещения.
– (путь) перемещения. тела на S параллельных сечений.
тела на S параллельных сечений.


