
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 4. Начала математического анализаСодержание книги
Поиск на нашем сайте
Тема 4.1. Понятие о пределах. Производная функции Понятие о пределе последовательности.Существование предела монотонной ограниченной последовательности. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма. Теоремы о пределах последовательностей. Переход к пределам в неравенствах. Понятие о непрерывности функции. Основные теоремы о непрерывных функциях. Понятие о пределе функции в точке. Поведение функций на бесконечности. Асимптоты. Понятие о производной функции, физический и геометрический смысл производной.Уравнение касательной к графику функции. Производные суммы, разности, произведения и частного. Производные основных элементарных функций. Производные сложной и обратной функций. Вторая производная. Применение производной к исследованию функций и построению графиков. Использование производных при решении уравнений и неравенств, текстовых, физических и геометрических задач, нахождении наибольших и наименьших значений. Примеры использования производной для нахождения наилучшего решения в прикладных задачах. Нахождение скорости для процесса, заданного формулой или графиком. Вторая производная и ее физический смысл.
Предел функции. Число Это определение означает, что L есть предел функции Пример. Найти Решение. Подставляя Сокращение дроби в данном случае корректно, так как приближается к 3. Теперь мы имеем: Некоторые замечательные пределы.
Бесконечно малая и бесконечно большая величины. Если предел некоторой переменной равен 0, то эта переменная называется бесконечно малой. Пример. Функция Бесконечно большая величина не имеет конечного предела, но она имеет так называемый бесконечный предел, что записывается как:
Символ
Наоборот, функция В соответствии с этим, результат в нашем примере можно записать так:
Числовой последовательностью называется бесконечное множество чисел Число А называется пределом последовательности (1), если для любого Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся. Для сходящихся последовательностей имеют место теоремы:
Пример. Найти общий член последовательности 1, 4, 9, 16, 25, … Решение: нетрудно видеть, что
Следовательно Пример. Найти общий член последовательности Решение: не трудно видеть, что
Следовательно:
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 868; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.49.19 (0.006 с.) |

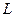 называется пределом функции
называется пределом функции  при
при  , стремящемся к
, стремящемся к  :
: 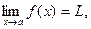 если для любого
если для любого 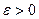 найдётся такое положительное число
найдётся такое положительное число 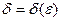 , зависящее от
, зависящее от 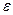 , что из условия
, что из условия 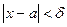 следует
следует 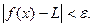
 , если значение функции неограниченно приближается к
, если значение функции неограниченно приближается к 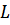 , когда значение аргумента
, когда значение аргумента 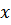 приближается к
приближается к 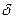 , что если
, что если 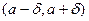 , то значение функции лежит в интервале
, то значение функции лежит в интервале 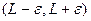 .Отметим, что в соответствии с этим определением аргумент функции лишь приближается к
.Отметим, что в соответствии с этим определением аргумент функции лишь приближается к 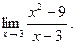
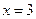 в выражение
в выражение 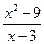 получим не имеющее смысла выражение
получим не имеющее смысла выражение 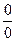 . Поэтому решим по-другому:
. Поэтому решим по-другому: 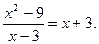
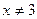 , он лишь
, он лишь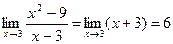 поскольку, если
поскольку, если 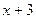 стремится к 6.
стремится к 6.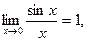
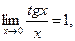
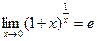 .
.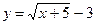 является бесконечно малой при
является бесконечно малой при 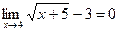 .Если абсолютное значение некоторой переменной неограниченно возрастает, то эта переменная называется бесконечно большой.
.Если абсолютное значение некоторой переменной неограниченно возрастает, то эта переменная называется бесконечно большой.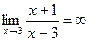 .
. («бесконечность») не означает некоторого числа, он означает только, что дробь неограниченно возрастает при
(«бесконечность») не означает некоторого числа, он означает только, что дробь неограниченно возрастает при 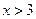 ), так и отрицательной (при
), так и отрицательной (при 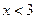 ). Если бесконечно большая величина может быть только положительной при любых значениях
). Если бесконечно большая величина может быть только положительной при любых значениях 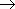 0 функция
0 функция 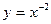 бесконечно большая, но она положительна как при
бесконечно большая, но она положительна как при 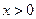 , так и при
, так и при 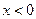 ; это выражается так:
; это выражается так: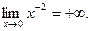
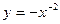 всегда отрицательна, поэтому
всегда отрицательна, поэтому 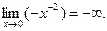
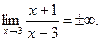
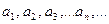 (1), следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого
(1), следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого  , задается как функция целочисленного аргумента,
, задается как функция целочисленного аргумента,  т.е.
т.е. 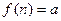 .
.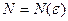 , такое, что при
, такое, что при 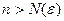 выполняется неравенство
выполняется неравенство 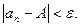 Если число
Если число 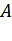 есть предел последовательности (1), то пишут
есть предел последовательности (1), то пишут 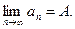
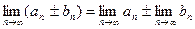
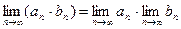
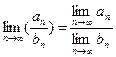 , если
, если 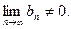
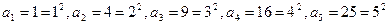 и т.д.
и т.д.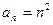 .
.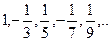
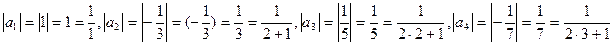 и т.д.
и т.д. .
.


