Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Возрастание и убывание функций.Содержание книги
Поиск на нашем сайте
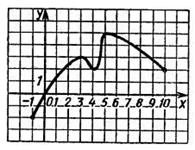
Познакомимся на примере с возрастанием и убыванием функции. На рисунке ниже изображен график функции, определенной на отрезке [-1;10]. Эта функция возрастает на отрезках [-1;3] и [4;5], и убывает на отрезках [3;4] и [5,10].
Рассмотрим еще один пример. Очевидно, что функция Определение. Функция Определение. Функция Экстремум функции. Введем понятие окрестности точки. Окрестностью точки Посмотрим на график на рисунке ниже.
Максимум и минимум функции. Приведем точные определения точек экстремума. Определение. Точка x0 называется точкой минимума функции Это наглядно показано на рисунке:
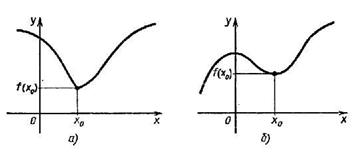
Определение. Точка x0 называется точкой максимума функции Это наглядно показано на рисунке:
Для точек минимума и максимума функции есть общее определение – точки экстремума. Значение функции в этих точках соответственно называется максимумом или минимумом этой функции. Общее название – экстремум функции. Точки максимума обычно обозначают Асимптоты Если график функции
Прямая
Прямая Обратные функции Понятие обратной функции применимо к функциям, обладающим следующим свойством: каждому значению Функция Функции Область определения функции Графики взаимно обратных функций симметричны друг другу относительно прямой Нахождение формулы для функции, обратной данной Заменить Пример. Найти формулу для функции, обратной функции: Заменить Функция f(x) называется функцией целочисленного аргумента, если множество значений x, для которых она определена, является множеством всех натуральных чисел 1, 2, 3,… Примером функции целочисленного аргумента может служить сумма n первых чисел натурального ряда. В данном случае
Функция 1. 2. 3. 4. функция нечетная, то есть 5. 6. 7. 8. 9. Функция 1. 2. 3. 4. функция ни четная, ни нечетная, то есть 5. 6. 7. 8. Функция 1. 2. 3. 4. функция нечетная, то есть 5. 6. 7. 8. график функции имеет 2 асимптоты: Функция 1. 2. 3. 4. функция ни четная, ни нечетная, то есть 5. 6. 7. график функции имеет 2 асимптоты:
График функции Графиком функции Подмножество координатной плоскости является графиком какой-либо функции, если оно имеет не более одной общей точки с любой прямой, параллельной оси OY. Например, множество, изображенное на рисунке ниже, не является графиком функции, так как оно содержит две точки с одной и той же абсциссой
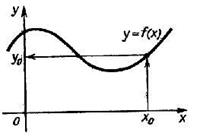
Графический способ задания зачастую удобнее по сравнению с аналитическим, так как по графику сразу видно, что из себя представляет функция и можно проанализировать ее поведение. Плюс ко всему для любого x0 из области определения легко найти (с определенной точностью) соответствующее значение y 0= f (x 0) функции. Это показано на рисунке ниже.
Тема 3.2. Степенная, тригонометрическая, показательная и логарифмическая функции. Преобразования графиков Степенная функция с натуральным показателем, ее свойства и график. Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций. Тригонометрические функции, их свойства и графики, периодичность, основной период. Обратные тригонометрические функции, их свойства и графики. Показательная функция (экспонента), ее свойства и график. Логарифмическая функция, ее свойства и график. Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой y = x, растяжение и сжатие вдоль осей координат. Показательные функции: Определение. Функция, заданная формулой 1. Область определения – множество 2. Область значений – множество 3. При 4. Является функцией общего вида.
Рис. 1 График функции
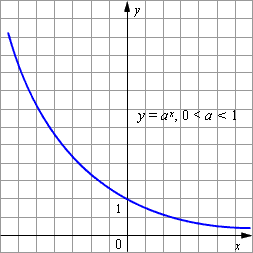
Рис. 2 График функции Основные свойства показательной функции · Область определения функции - вся числовая прямая. · Область значений функции – промежуток · Функция строго монотонно возрастает на всей числовой прямой, то есть, если · При · Если Графики показательных функций с основанием
Основные свойства показательной функции · Область определения функции - вся числовая прямая. · Область значений функции – промежуток · Функция строго монотонно возрастает на всей числовой прямой, то есть, если
· При · Если К общим свойствам показательной функции как при
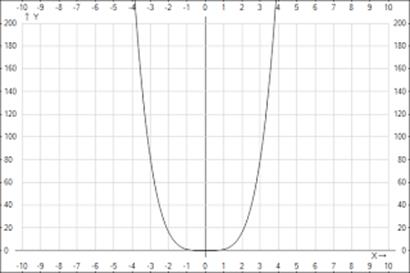
Показатель В этом случае степенная функция · область определения – все действительные числа, т. е. множество R; · множество значений – неотрицательные числа, т. е. · функция · функция является убывающей на промежутке График функции
Показатель В этом случае степенная функция · область определения – множество R; · множество значений – множество R; · функция · функция является возрастающей на всей действительной оси. График функции
Показатель В этом случае степенная функция · область определения – множество · множество значений – положительные числа · функция · функция является возрастающей на промежутке График функции
Показатель В этом случае степенная функция · область определения – множество · множество значений – множество · функция · функция является убывающей на промежутках График функции
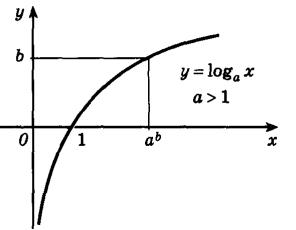
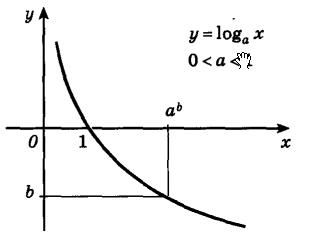
Логарифмическая функция Функцию вида Основные свойства логарифмической функции: 1. Областью определения логарифмической функции будет являться все множество положительных вещественных чисел. Для краткости его еще обозначают 2. Областью значения логарифмической функции будет являться все множество вещественных чисел. 3. Если основание логарифмической функции
4. График логарифмической функции всегда проходит через точку (1;0). 5. Возрастающая логарифмическая функция, будет положительной при 6. Убывающая логарифмическая функция, будет отрицательной при
На следующем рисунке представлен график убывающей логарифмической функции –
7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вид. 8. Функция не имеет точек максимума и минимума. Если построить в одной оси координат показательную и логарифмическую функции с одинаковыми основаниями, то графики этих функций будут симметричны относительно прямой
Изложенное выше утверждение будет справедливо, как для возрастающих, так и для убывающих логарифмических и показательных функций. Рассмотрим пример: найти область определения логарифмической функции Исходя из свойств логарифмической функции, областью определения является все множество положительных вещественных чисел R+. Тогда заданная функция будет определена для таких Таким образом, получается, что областью определения функции
Преобразования графиков функции. Параллельный перенос вдоль оси абсцисс. Преобразование координат точки с координатами именно при этих значениях График функции В качестве примера, ниже приведен график функции
Растяжение и сжатие вдоль оси абсцисс. Такое преобразование задается формулами: Произвольная точка графика функции По определению графика функции (см. выше) эта фигура есть график функции Правило: для построения графика функции Параллельный перенос вдоль оси ординат. Обозначим Возьмем произвольную функцию
Исходя из определения графика функции (см. выше), эта фигура является графиком функции Для построения графика функции В качестве примера ниже приведен график
Растяжение и сжатие вдоль оси ординат. Рассмотрим растяжение вдоль оси OY с коэффициентом Для построения точки
Для примера на рисунке ниже показано построение точек, в которые переходят данные точки с
Теперь выясним, в какую фигуру переходит график Резюмируя вышеизложенное, сформулируем правило: Для построения графика функции В качестве примера, ниже приведен график функции
Параллельный перенос вдоль оси абсцисс. Преобразование координат точки с координатами Именно при этих значениях График функции В качестве примера, ниже приведен график функции
Растяжение и сжатие вдоль оси абсцисс. Такое преобразование задается формулами: Произвольная точка графика функции | |||||||||||||||
|
| Поделиться: |

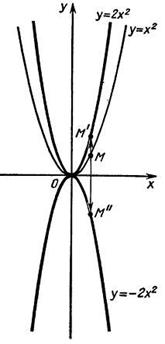
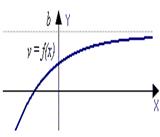
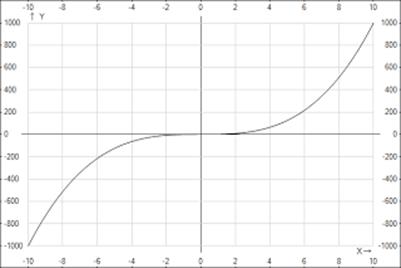
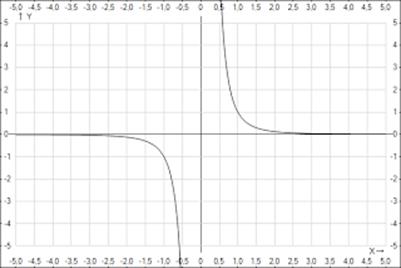
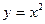 убывает на промежутке (-∞; 0] и возрастает на промежутке [0;∞). Видно, что график этой функции при изменении
убывает на промежутке (-∞; 0] и возрастает на промежутке [0;∞). Видно, что график этой функции при изменении  от -∞ до 0 сначала опускается до нуля, а затем поднимается до бесконечности.
от -∞ до 0 сначала опускается до нуля, а затем поднимается до бесконечности. возрастает на множестве P, если для любых
возрастает на множестве P, если для любых  и
и 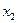 из множества P, таких, что
из множества P, таких, что 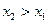 выполнено неравенство
выполнено неравенство 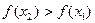 .
.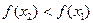 .
.  называется любой интервал, содержащий эту точку. Например, интервал (2; 6) - это окрестность точки 3.
называется любой интервал, содержащий эту точку. Например, интервал (2; 6) - это окрестность точки 3.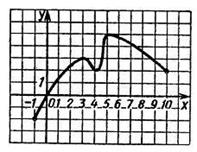
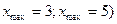 и точками минимума
и точками минимума 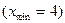 . При построении графиков функций полезно сначала найти точки максимума и минимума. Например, в случае функции синуса точки вида
. При построении графиков функций полезно сначала найти точки максимума и минимума. Например, в случае функции синуса точки вида 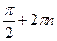 - это точки максимума, а точки вида
- это точки максимума, а точки вида 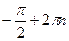 - это точки минимума. В дальнейшем изложении будет показано, как искать точки максимума и минимума функции, не прибегая к рисованию графиков. Точки максимума и минимума функции называют точками экстремума функции.
- это точки минимума. В дальнейшем изложении будет показано, как искать точки максимума и минимума функции, не прибегая к рисованию графиков. Точки максимума и минимума функции называют точками экстремума функции.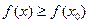 .
.
 выполняется неравенство
выполняется неравенство 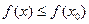 .
.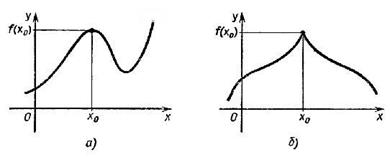
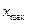 , а точки минимума –
, а точки минимума – 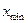 .
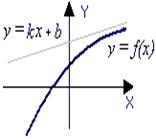
. имеет бесконечную ветвь (ветви), у графика могут быть асимптоты. Асимптотой графика называется прямая, к которой неограниченно приближается точка графика при удалении этой точки по бесконечной ветви.
имеет бесконечную ветвь (ветви), у графика могут быть асимптоты. Асимптотой графика называется прямая, к которой неограниченно приближается точка графика при удалении этой точки по бесконечной ветви.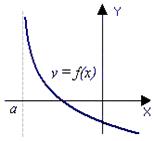
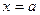
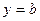
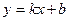
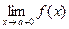 (предел справа) или
(предел справа) или 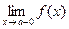 (предел слева) равен бесконечности.
(предел слева) равен бесконечности.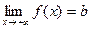 или
или 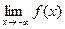 . Прямая
. Прямая 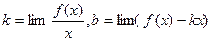 либо при
либо при 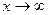 , либо при
, либо при 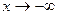 .
. из области определения соответствует единственное значение
из области определения соответствует единственное значение 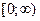 , для функции
, для функции 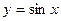 – отрезок
– отрезок 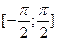 ).
). называется обратной для функции
называется обратной для функции 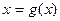 .
.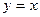 .
.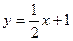 .
.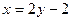 .
.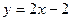 .
.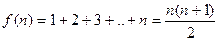 .
.
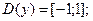



 при
при  ;
; при
при  ;
; при
при  ;
;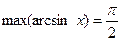 при
при  ;
; при
при  .
.
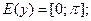

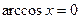 при
при  ;
; при
при  ;
; при
при  при
при  .
.




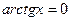 при
при  при
при  ;
; при
при  ;
;
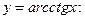


 ни при каких
ни при каких  ;
; при
при  ;
;
 координатной плоскости, где
координатной плоскости, где 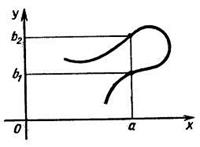
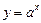 (где
(где 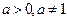 ), называется показательной функцией с основанием
), называется показательной функцией с основанием  . Сформулируем основные свойства показательнойфункции:
. Сформулируем основные свойства показательнойфункции: всех действительных чисел.
всех действительных чисел. всех положительных действительных чисел.
всех положительных действительных чисел. функция возрастает на всей числовой прямой; при
функция возрастает на всей числовой прямой; при 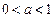 функция убывает.
функция убывает.
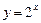 , на интервале
, на интервале  .
.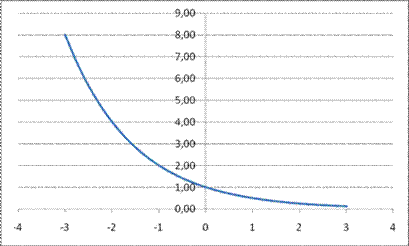
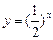 , на интервале
, на интервале 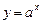 при
при 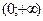 .
.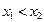 , то
, то 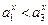 .
.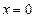 значение функции равно 1.
значение функции равно 1.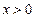 , то
, то 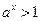 и если
и если 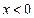 , то
, то 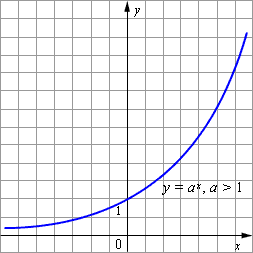
 .
.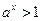 .
.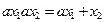 , для всех
, для всех 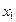 и
и 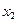 ;
;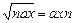 для любого
для любого 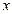 и любого
и любого 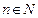 ;
;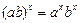 для любых
для любых 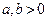 ;
;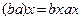 для любых
для любых 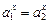 , то
, то 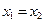 .
.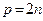 – четное натуральное число.
– четное натуральное число.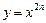 , где
, где 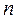 – натуральное число, обладает следующими свойствами:
– натуральное число, обладает следующими свойствами: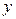 больше или равно 0;
больше или равно 0;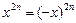 ;
;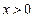 .
.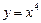 .
.
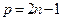 – нечетное натуральное число.
– нечетное натуральное число. , где натуральное число, обладает следующими свойствами:
, где натуральное число, обладает следующими свойствами: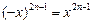 (- x)2n-1 = x2n-1;
(- x)2n-1 = x2n-1;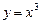 .
.
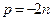 , где
, где 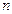 и – натуральное число.
и – натуральное число.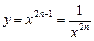 обладает следующими свойствами:
обладает следующими свойствами: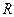 , кроме
, кроме 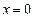 ;
;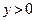 ;
;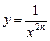 четная, так как
четная, так как 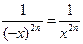 ;
;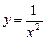 .
.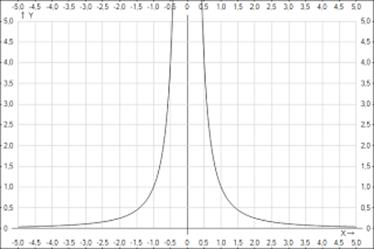
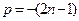 , где
, где 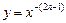 обладает следующими свойствами:
обладает следующими свойствами: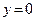 ;
;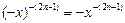 ;
;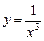 .
.
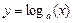 , где
, где 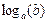 – данная запись будет обозначать логарифм
– данная запись будет обозначать логарифм  по основанию
по основанию 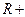 . Очевидное свойство, так как каждое положительное число имеет логарифм по основанию
. Очевидное свойство, так как каждое положительное число имеет логарифм по основанию 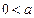
 , и отрицательной при
, и отрицательной при 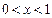 .
.
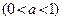 :
:
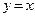 . Данное утверждение показано на следующем рисунке.
. Данное утверждение показано на следующем рисунке.
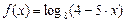 .
.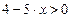 . Решаем это неравенство и получаем
. Решаем это неравенство и получаем 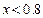 .
.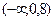 .
. , полученную из исходной точки при помощи параллельного переноса на вектор (a,0) вдоль оси абсцисс, задается формулами:
, полученную из исходной точки при помощи параллельного переноса на вектор (a,0) вдоль оси абсцисс, задается формулами: 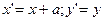 , согласно этим формулам каждая точка графика
, согласно этим формулам каждая точка графика 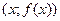 переходит в точку
переходит в точку 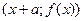 . С помощью переменных
. С помощью переменных 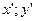 можно записать, что график функции
можно записать, что график функции 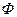 , состоящую из точек
, состоящую из точек 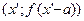 , где
, где 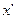 принимает все значения вида
принимает все значения вида 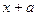 , причем
, причем  .
.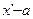 принадлежит
принадлежит 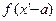 определено. Следовательно, фигура
определено. Следовательно, фигура 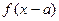 . Сформулируем правило:
. Сформулируем правило: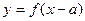 получается из графика
получается из графика 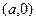 . Если
. Если  , то вектор
, то вектор  , то в отрицательном.
, то в отрицательном.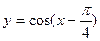 .
.
 .
.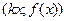 . Переходя к переменным
. Переходя к переменным 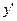 запишем, что график функции
запишем, что график функции 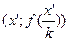 , где
, где 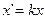 принимает все значения из области определения
принимает все значения из области определения 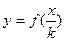 .
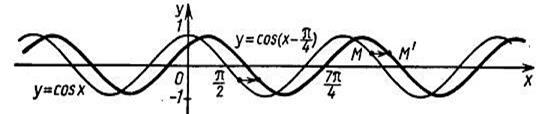
. вдоль оси абсцисс.
вдоль оси абсцисс.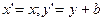 .
.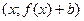 . Это означает, что график функции
. Это означает, что график функции 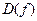 .
.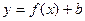 . Подводя черту под вышеизложенной теорией, сформулируем правило:
. Подводя черту под вышеизложенной теорией, сформулируем правило: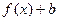 , где
, где  – постоянное число, надо перенести график функции
– постоянное число, надо перенести график функции 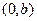 вдоль оси ординат.
вдоль оси ординат.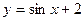 , который был получен из графика функции
, который был получен из графика функции 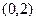 вдоль оси ординат ОУ.
вдоль оси ординат ОУ.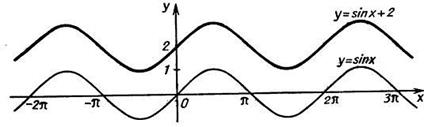
 .
. , в которую переходит данная точка
, в которую переходит данная точка  при растяжении, надо построить на прямой
при растяжении, надо построить на прямой  (см. рисунок ниже), где
(см. рисунок ниже), где  – проекция точки
– проекция точки  , точку, гомотетичную точке
, точку, гомотетичную точке 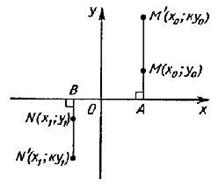
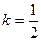 и 2.
и 2.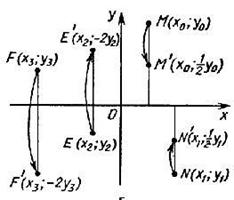
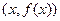 переходит в точку
переходит в точку 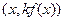 . Следовательно, график
. Следовательно, график 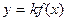 .
.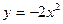 .
.