
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деление многочленов с остатком.Содержание книги
Поиск на нашем сайте
Многочлен Покажем этот алгоритм на примере:
Нахождение корней многочлена – интересная и достаточно трудная задача, решение которой выходит за границы школьного курса математики. Однако для многочленов с целыми коэффициентами есть простой переборный алгоритм, позволяющий находить все рациональные корни. Теорема. Если многочлен с целыми коэффициентами имеет рациональный корень Теорема Безу. Остаток от деления многочлена Следствие. Для того чтобы многочлен Схема Горнера. Схема Горнера – это алгоритм деления многочленов, записанный для частного случая, когда частное равно двучлену Построим этот алгоритм. Пусть
По определению деления с остатком
Корни многочленов Рассмотрим нахождение корней квадратного трехчлена с комплексными коэффициентами, то есть решение уравнения Выполняя те же действия, что и при решении квадратного уравнения, приходим к уравнению
Обозначив
Оказывается, что в поле комплексных чисел корни всегда существуют не только у квадратного трехчлена, но и у любого многочлена. Теорема. Любой многочлен ненулевой степени с комплексными коэффициентами имеет хотя бы один корень. Данная теорема по традиции называется основной теоремой алгебры. Доказательство ее достаточно сложное и поэтому здесь оно не приводится. Интересно выяснить, сколько корней имеет многочлен степени Теорема. Для любого многочлена ненулевой степени в поле комплексных чисел справедливо разложение на множители:
Очевидно, что в указанном разложении числа Из предыдущей теоремы легко получить теорему, дающую ответ на вопрос о числе корней многочлена. Теорема. В поле комплексных чисел любой многочлен ненулевой степени По вопросу практического нахождения корней стоит отметить следующее. Для нахождения корней многочленов третьей и четвертой степеней существуют формулы, позволяющие выразить корни многочлена через его коэффициенты. Для многочлена третьей степени - это формула Кардано. Нахождение корней многочлена четвертой степени сводится к нахождению корней многочлена третьей степени методом, принадлежащим Феррари. Для многочленов выше четвертой степени доказано, что их корни нельзя выразить через их коэффициенты с помощью радикалов. Однако, даже для многочленов третьей и четвертой степени, как правило, корни находят без использования указанных выше формул, так как те дают очень громоздкие выражения. Обычно корни находят приближенно, с помощью различных вычислительных алгоритмов. Формулы сокращенного умножения Квадрат суммы двух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй: Квадрат разности двух величин равен квадрату первой минус удвоенное произведение первой на вторую плюс квадрат второй: Произведение суммы двух величин на их разность равно разности их квадратов: Куб суммы двух величин равен кубу первой плюс утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй плюс куб второй: Куб разности двух величин равен кубу первой минус утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй минус куб второй: Произведение суммы двух величин на неполный квадрат разности равно сумме их кубов: Произведение разности двух величин на неполный квадрат суммы равно разности их кубов: Формула бинома Ньютона
Если Функция Пример. Многочлен от двух переменных Тема 1.4. Корни и степени Корень степени n>1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем.
Алгебраические выражения, содержащие операцию извлечения корня, называются иррациональными. Корнем По определению Основные свойства корня Если корни рассматривать на множестве действительных чисел, то: а) корень четной степени из положительного числа имеет два значения, равные по абсолютной величине и противоположные по знаку; б) корень четной степени из отрицательного числа на множестве действительных чисел не существует; в) корень нечетной степени из положительного числа имеет только одно действительное значение, которое положительно; г) корень нечетной степени из отрицательного числа имеет только одно действительное значение, которое отрицательно; д) корень любой натуральной степени из нуля равен нулю. Действие, посредством которого отыскивается корень Арифметический корень и его свойства Арифметическим значением корня или арифметическим корнем степени Множество неотрицательных действительных чисел замкнуто относительно извлечения арифметического корня, а результат этого действия однозначен. Это значит, что для любого неотрицательного числа Степень с рациональным показателем Степенью числа Например, Степень числа по определению Замечания 1. Из определения степени с рациональным показателем следует, что для любого положительного а и любого рационального 2. Любое рациональное число допускает различные записи его в виде дроби, поскольку 3. При Для степеней с рациональным показателем сохраняются основные свойства степеней, верные для любых показателей (при условии, что основание степени будет положительным). Степень с действительным показателем. Итак, для любого действительного числа мы определили операцию возведения в натуральную степень; для любого числа Возникает естественный вопрос: можно ли каким-либо образом определить операцию возведения в иррациональную степень, а, следовательно, определить смысл выражения 1. Если 2. Если Но Под 3. Если Тема 1.5. Логарифм Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число е. Определение. Логарифмом числа Другими словами, логарифм числа Для логарифма числа Таким образом, для всех действительных чисел При Наиболее широкое применение нашли следующие виды логарифмов. • Натуральные: • Десятичные: • Двоичные: Основное логарифмическое тождество Из определения логарифма следует основное логарифмическое тождество:
Следствие: из равенства двух вещественных логарифмов следует равенство логарифмируемых выражений. В самом деле, если Логарифмы единицы и числа, равного основанию Два равенства, очевидных из определения логарифма:
Существует формулы на случай, когда допускаются отрицательные значения переменных, например:
Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:
Замена основания логарифма Логарифм
Следствие (при
Логарифмическая функция обратна к показательной. Тема 1.6. Преобразования простейших выражений Преобразования выражений, включающих арифметические операции, а также операции возведения в степень и логарифмирования.
Операции сложения и умножения действительных (а значит, в том числе и натуральных, и целых) чисел обладают следующими свойствами: 1. 2. 3. 4. 5. Переместительные законы также называются также коммутативными. Их смысл в том, что результат не меняется при перестановке слагаемых или сомножителей. Переместительный (коммутативный) закон сложения: Переместительный (коммутативный) закон умножения: Сочетательные законы также называют ассоциативными. Их смысл в том, что результат не меняется при группировке слагаемых или сомножителей. Сочетательный (ассоциативный) закон сложения: Сочетательный (ассоциативный) закон умножения: Распределительные законы также называют дистрибутивными. Их смысл для операции произведения заключается в том, что операцию произведения можно выполнить по частям – для каждого слагаемого, входящего во второй сомножитель. Распределительный (дистрибутивный) закон умножения относительно сложения: Также существует распределительный (дистрибутивный) закон умножения относительно вычитания: Рассмотрим несколько примеров. Пример. Упростите выражение
Решение.
Пример. Вычислить Решение. Ответ. 1. Пример. Упростить выражение Решение. Ответ. 3. Пример. Найти значение выражения Решение.
Ответ. 1. Пример. Вычислить Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифм произведения:
Ответ. Пример. Вычислить Решение. Преобразуем данное выражение, используя свойство суммы логарифмов и определение натурального логарифма:
Ответ.
Раздел 2. Тригонометрия Тема 2.1. Тригонометрические функции и преобразования тригонометрических выражений Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества. Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента.
Введем понятие единичной окружности. Определение. Окружность с центром в начале координат и радиусом равным единице называется единичной. За начало отсчета возьмем точку с координатами (1;0). Поворот против часовой стрелки будем считать положительным, а по часовой стрелке отрицательным. Повернемся на
Определение. Синусом числа Определение. Косинусом числа Определение. Тангенсом числа Определение. Котангенсом числа Нужно отметить, что Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («∞» означает, что функция в указанной точке не определена, а в её окрестности стремится к бесконечности).
Значения косинуса и синуса на окружности.
1) Рассмотрим Из курса геометрии нам известно, что катет, лежащий против угла в Воспользуемся теоремой Пифагора. ОВ 2 = ОА 2 – АВ 2=12–
Воспользуемся определением тангенса
По определению котангенса
Задание. Самостоятельно найти значение тригонометрических функций для Существует таблица значений тригонометрических функций, которой можно пользоваться для решения примеров.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 5081; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.134.18 (0.011 с.) |

 можно разделить на многочлен
можно разделить на многочлен  с остатком. Под этим понимают, что
с остатком. Под этим понимают, что  , где степень остатка
, где степень остатка  строго меньше степени делителя
строго меньше степени делителя  (или остаток равен нулю). Возможность такого представления следует из алгоритма «деления углом», который аналогичен делению целых чисел «столбиком».
(или остаток равен нулю). Возможность такого представления следует из алгоритма «деления углом», который аналогичен делению целых чисел «столбиком».

 (
( - несократимая дробь), то числитель дроби является делителем свободного члена, а знаменатель – делителем старшего коэффициента этого многочлена.
- несократимая дробь), то числитель дроби является делителем свободного члена, а знаменатель – делителем старшего коэффициента этого многочлена. равен значению многочлена в точке а, т. е. числу
равен значению многочлена в точке а, т. е. числу  .
. , т. е. чтобы а было корнем многочлена
, т. е. чтобы а было корнем многочлена  .
. – делимое,
– делимое, – частное (его степень, очевидно, будет на 1 меньше),
– частное (его степень, очевидно, будет на 1 меньше),  – остаток (так как деление осуществляется на многочлен 1 – ой степени, то степень остатка будет на 1 меньше, то есть нулевая, значит, остаток – константа).
– остаток (так как деление осуществляется на многочлен 1 – ой степени, то степень остатка будет на 1 меньше, то есть нулевая, значит, остаток – константа). . После подстановки выражений многочленов получим:
. После подстановки выражений многочленов получим: .
. , где
, где  – комплексные числа,
– комплексные числа,  .
. .
. , получим уравнение
, получим уравнение  , где
, где  . Такое уравнение мы умеем решать. В результате получатся два корня, если
. Такое уравнение мы умеем решать. В результате получатся два корня, если  , и один, если
, и один, если  . Так как
. Так как  равен нулю, то количество корней определяется тем же условием: равен дискриминант нулю или нет. Кроме того, заметим, что если
равен нулю, то количество корней определяется тем же условием: равен дискриминант нулю или нет. Кроме того, заметим, что если  , то
, то  и
и  . Поэтому корни уравнения
. Поэтому корни уравнения  можно записать в виде
можно записать в виде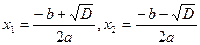 , где
, где  означает одно из решений (любое!) уравнения
означает одно из решений (любое!) уравнения  . Отметим, что формулы также можно записать в виде, так как при вещественном
. Отметим, что формулы также можно записать в виде, так как при вещественном  выполнено
выполнено  .
. . Мы уже знаем, что если
. Мы уже знаем, что если  , то корень один, если
, то корень один, если  имеет ровно
имеет ровно  различных корней, если
различных корней, если  .
.
 являются корнями многочлена и других корней у него быть не может. Однако среди чисел
являются корнями многочлена и других корней у него быть не может. Однако среди чисел  , то
, то  - корень кратности 2,
- корень кратности 2,  и
и  - корни кратности 1 или, иначе, простые корни.
- корни кратности 1 или, иначе, простые корни. .
. .
. .
. .
. .
. .
. .
.



 -й член (
-й член ( -е слагаемое) разложения степени бинома обозначать через
-е слагаемое) разложения степени бинома обозначать через  , то
, то  .
. называется симметрической, если для
называется симметрической, если для  выполнено равенство
выполнено равенство  .
. является симметрической функцией. В самом деле,
является симметрической функцией. В самом деле,  .
. -й степени из числа
-й степени из числа  называется такое число
называется такое число  ,
,  ). Обозначается
). Обозначается  , где
, где  ).
). , если
, если  , или
, или  .
. .
. ) всегда найдется, и притом только одно, такое неотрицательное число
) всегда найдется, и притом только одно, такое неотрицательное число  .
. с рациональным показателем
с рациональным показателем  , где
, где  – целое число, а
– целое число, а  .
. .
. определена только для положительных показателей;
определена только для положительных показателей; , для любого
, для любого  .
.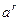 положительно.
положительно. для любого натурального
для любого натурального  также не зависит от формы записи рационального числа
также не зависит от формы записи рационального числа  рациональная степень числа
рациональная степень числа  мы определили возведения в нулевую и целую отрицательную степень; для любого
мы определили возведения в нулевую и целую отрицательную степень; для любого  мы определили операцию возведения в положительную дробную степень; для любого
мы определили операцию возведения в положительную дробную степень; для любого  мы определили операцию возведения в отрицательную дробную степень.
мы определили операцию возведения в отрицательную дробную степень. и для любого действительного числа
и для любого действительного числа  , где
, где  - иррациональное число. Для этого нужно рассмотреть три случая:
- иррациональное число. Для этого нужно рассмотреть три случая:  .
.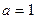 , то по определению полагают, что
, то по определению полагают, что  .
. , то выберем любое рациональное число
, то выберем любое рациональное число  и любое рациональное число
и любое рациональное число  . Тогда, очевидно,
. Тогда, очевидно,  и, следовательно:
и, следовательно:  .
. и потому (так как
и потому (так как  и, наконец,
и, наконец,  .
. понимают такое число, которое лежит между
понимают такое число, которое лежит между 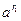 и
и  при любом выборе чисел
при любом выборе чисел  и
и  обладающих свойством
обладающих свойством  . Можно доказать, что число
. Можно доказать, что число  и любого иррационального
и любого иррационального  , то выберем любое рациональное число
, то выберем любое рациональное число  и, следовательно,
и, следовательно,  (это неравенство доказывается аналогично приведённому выше для
(это неравенство доказывается аналогично приведённому выше для  . Можно доказать, что число
. Можно доказать, что число  называют такую степень, в которую надо возвести число
называют такую степень, в которую надо возвести число  .
. .
. , которое часто называют основным логарифмическим тождеством.
, которое часто называют основным логарифмическим тождеством. это уравнение не имеет решения, а при
это уравнение не имеет решения, а при  любое число является решением; в обоих случаях логарифм не определён. Аналогично заключаем, что логарифм не существует при нулевом или отрицательном
любое число является решением; в обоих случаях логарифм не определён. Аналогично заключаем, что логарифм не существует при нулевом или отрицательном  ; кроме того, значение показательной функции
; кроме того, значение показательной функции  всегда положительно, поэтому следует исключить также случай отрицательного
всегда положительно, поэтому следует исключить также случай отрицательного  . Окончательно получаем: вещественный логарифм
. Окончательно получаем: вещественный логарифм  имеет смысл при
имеет смысл при  .
. , основание: число Эйлера
, основание: число Эйлера  .
. , основание: число
, основание: число  .
. , основание:
, основание:  .
. .
. , то
, то  , откуда, согласно основному тождеству:
, откуда, согласно основному тождеству:  .
. .
. ;
; .
.
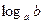 по основанию
по основанию  можно преобразовать в логарифм по другому основанию
можно преобразовать в логарифм по другому основанию  :
: .
. .
.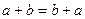 (переместительный закон сложения).
(переместительный закон сложения). (сочетательный закон сложения).
(сочетательный закон сложения). (переместительный закон умножения).
(переместительный закон умножения). (сочетательный закон умножения).
(сочетательный закон умножения). (распределительный закон умножения относительно сложения).
(распределительный закон умножения относительно сложения).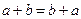 . Сумма не меняется от перестановки её слагаемых.
. Сумма не меняется от перестановки её слагаемых. . Произведение не меняется от перестановки его сомножителей.
. Произведение не меняется от перестановки его сомножителей. . Произведение не зависит от группировки его сомножителей.
. Произведение не зависит от группировки его сомножителей. .
. .
. .
.
 при
при  ,
,  .
.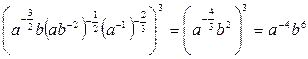 . Подставляем
. Подставляем  ,
,  , получим
, получим  .
. и вычислить его значение при
и вычислить его значение при  и
и  .
. . При
. При  и
и  значение данного выражения равно
значение данного выражения равно  .
. при
при  и
и  .
. ,
,  подставляем в данное выражение:
подставляем в данное выражение:
 , если
, если  .
.
 .
. .
.

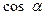 . Координата по оси OY – ордината, ее мы назовем синусом числа
. Координата по оси OY – ордината, ее мы назовем синусом числа 
 =
=  ,
, 
 =
=  , sin
, sin 

 Тангенс и котангенс могут принимать любые значения.
Тангенс и котангенс могут принимать любые значения.













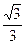




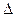 ОАВ, он прямоугольный, угол АОВ =
ОАВ, он прямоугольный, угол АОВ =  .
. равен половине гипотенузы. Т.к. окружность единичная, то ОА =1, значит АВ =
равен половине гипотенузы. Т.к. окружность единичная, то ОА =1, значит АВ =  . Но АВ равняется ординате точки
. Но АВ равняется ординате точки  , значит sin
, значит sin  =
=  =1–
=1–  =
= . ОВ =
. ОВ =  . Т. к. ОВ =
. Т. к. ОВ =  , значит
, значит  .
. =
=  :
:  =
= 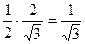 .
.




