
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7. 1. Геометрия на плоскостиСодержание книги
Поиск на нашем сайте
Свойство биссектрисы угла треугольника. Решение треугольников. Вычисление биссектрис, медиан, высот, радиусов вписанной и описанной окружностей. Формулы площади треугольника: формула Герона, выражение площади треугольника через радиус вписанной и описанной окружностей. Вычисление углов с вершиной внутри и вне круга, угла между хордой и касательной. Теорема о произведении отрезков хорд. Теорема о касательной и секущей. Теорема о сумме квадратов сторон и диагоналей параллелограмма Вписанные и описанные многоугольники. Свойства и признаки вписанных и описанных четырехугольников. Геометрические места точек. Решение задач с помощью геометрических преобразований и геометрических мест. Теорема Чевы и теорема Менелая. Эллипс, гипербола, парабола как геометрические места точек. Неразрешимость классических задач на построение. Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а Биссектриса Биссектриса угла – это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника. Свойства биссектрис треугольника · Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон. · Биссектрисы внутренних углов треугольника пересекаются в одной точке. Это точка называется центром вписанной окружности. · Биссектрисы внутреннего и внешнего углов перпендикулярны. · Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трех вневписанных окружностей этого треугольника. · Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника. · Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой. Решение треугольников
У треугольника общего вида имеется 6 основных характеристик: 3 линейные (длины сторон Алгоритм решения задачи зависит от того, какие именно характеристики треугольника считаются известными. Далее будем символически обозначать заданные величины · Три стороны (ССС); · Две стороны и угол между ними (СУС); · Две стороны и угол не между ними (ССУ); · Сторона и два прилежащих угла (УСУ); · Сторона, противолежащий угол и один из прилежащих (УУС). Основные теоремы Стандартным методом решения задачи является использование нескольких фундаментальных соотношений, выполняющихся для всех плоских треугольников: Теорема косинусов
Теорема синусов
Сумма углов треугольника
Теорема тангенсов (применяется редко)
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 812; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.210.83 (0.01 с.) |

 отрезки - его сторонами.
отрезки - его сторонами. ) и 3 угловые
) и 3 угловые  . В классической задаче плоской тригонометрии заданы 3 из этих 6 характеристик, и нужно определить 3 остальные. Очевидно, если известны только 2 или 3 угла, однозначного решения не получится, так как любой треугольник, подобный данному, тоже будет решением, поэтому будем считать, что хотя бы одна из известных величин – линейная.
. В классической задаче плоской тригонометрии заданы 3 из этих 6 характеристик, и нужно определить 3 остальные. Очевидно, если известны только 2 или 3 угла, однозначного решения не получится, так как любой треугольник, подобный данному, тоже будет решением, поэтому будем считать, что хотя бы одна из известных величин – линейная. (сторона) и
(сторона) и  (угол). Поскольку сочетание УУУ исключено из рассмотрения, остаются 5 различных вариантов:
(угол). Поскольку сочетание УУУ исключено из рассмотрения, остаются 5 различных вариантов:
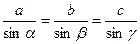

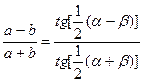 .
.



