
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Текстовые задачи на целые числаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Текстовые задачи, в которых используются свойства целых чисел, всегда являются достаточно сложными. Здесь на помощь приходят свойства целых чисел, изложенные выше. Пример. В первой коробке были только красные шары, а во второй – только синие шары. Число красных шаров составляло от числа синих шаров. Когда из коробки удалили соответственно Решение. Пусть В первой коробке осталось Во второй коробке осталось Получаем систему неравенств: Число Из промежутка Ответ. 1575 шаров и 1995 шаров. Пример. Рота солдат прибыла на парад в полном составе прямоугольным строем по 24 человека в ряд. По прибытии оказалось, что не все солдаты могут участвовать в параде. Оставшийся для парада состав роты перестроили так, что число рядов стало на два меньше прежнего, а число солдат в каждом ряду стало на 26 больше числа новых рядов. Известно, что если бы все солдаты участвовали в параде, то роту можно было бы выстроить так, чтобы число солдат в каждом ряду равнялось числу рядов. Сколько солдат было в роте? Решение. Пусть Ответ: 144 человека. Тема 1.2 Комплексные числа Комплексные числа. Геометрическая интерпретация комплексных чисел. Действительная и мнимая часть, модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы записи комплексных чисел. Арифметические действия над комплексными числами в разных формах записи. Комплексно сопряженные числа. Возведение в натуральную степень (формула Муавра). Основная теорема алгебры. Определение. Числа вида Посмотрим, какие действия арифметики можно производить с комплексными числами. Сложение чисел должно удовлетворять обычным правилам, поэтому:
При вычислении произведения скобки раскроем привычным способом:
Так как
Итак, результаты сложения и умножения комплексных чисел снова оказались комплексными числами. Операцию вычитания определить не сложно:
Рассмотрим операцию деления. Учтем, что при умножении числителя и знаменателя дроби на одно и то же число дробь не меняется:
Так как
Результат деления двух комплексных чисел оказывается снова комплексным числом. Как видно из полученной формулы, деление нельзя выполнить лишь в том случае, когда Итак, мы вроде бы расширили множество вещественных чисел. Но есть в этом построении один существенный пробел. Мы предположили, что есть такое число Очевидно, что комплексное число, как оно было определено раньше, – просто другая форма записи пары вещественных чисел Однако в математике, в силу традиции, используется запись комплексного числа
Число Замечание. В электротехнике, где буква Если операции сложения, вычитания и умножения комплексных чисел соответствуют обычным правилам раскрытия скобок, то для выполнения деления нужно или запомнить формулу (4), или, что проще, каждый раз при выполнении деления умножать числитель и знаменатель дроби на число, сопряженное знаменателю. Пример. Пусть
Вычислим еще
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 904; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.220.239 (0.006 с.) |

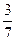 и
и 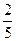 бывших там шаров, то в первой коробке осталось менее 1000 шаров, а во второй – более 1000 шаров. Определить, сколько шаров было в каждой коробке первоначально.
бывших там шаров, то в первой коробке осталось менее 1000 шаров, а во второй – более 1000 шаров. Определить, сколько шаров было в каждой коробке первоначально. синих шаров было во второй коробке. Тогда в первой коробке было
синих шаров было во второй коробке. Тогда в первой коробке было 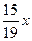 красных шаров.
красных шаров.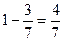 от первоначального числа шаров, т.е.
от первоначального числа шаров, т.е. 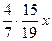 шаров. Это число меньше 1000.
шаров. Это число меньше 1000.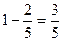 от первоначального числа шаров, т.е.
от первоначального числа шаров, т.е. 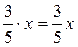 шаров. Это число больше 1000.
шаров. Это число больше 1000.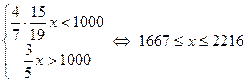 .
.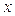 делится на 5,7 и 19. Поэтому число
делится на 5,7 и 19. Поэтому число 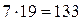 (так как 7 и 19 взаимно просты).
(так как 7 и 19 взаимно просты).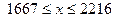 этим условиям удовлетворяет только х =1995. Тогда
этим условиям удовлетворяет только х =1995. Тогда 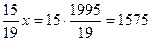 . В первой коробке было 1575 красных шаров, а во второй – 1995 синих шаров.
. В первой коробке было 1575 красных шаров, а во второй – 1995 синих шаров. – число рядов в роте при прибытии роты на парад. Численность роты
– число рядов в роте при прибытии роты на парад. Численность роты 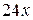 солдат. После перестройки роты рядов стало
солдат. После перестройки роты рядов стало 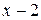 , а число солдат в новом ряду стало
, а число солдат в новом ряду стало 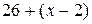 солдат. Для парада осталось
солдат. Для парада осталось 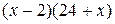 солдат. Число солдат, не участвующих в параде:
солдат. Число солдат, не участвующих в параде: 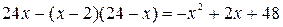 . Корни квадратного трехчлена
. Корни квадратного трехчлена 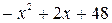 есть
есть 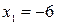 и
и 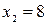 . Значит, выражение
. Значит, выражение 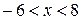 . По условию задачи
. По условию задачи 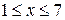 . Требуется подобрать такие натуральные
. Требуется подобрать такие натуральные 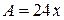 являлось полным квадратом. Имеем соответственно: А=24 при
являлось полным квадратом. Имеем соответственно: А=24 при 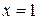 , А=48 при
, А=48 при 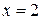 , А=72 при
, А=72 при 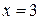 , А=96 при
, А=96 при 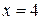 , А=120 при
, А=120 при 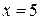 , А=144 при
, А=144 при 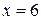 , А=168 при
, А=168 при 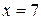 . Полным квадратом является только А=144, следовательно,
. Полным квадратом является только А=144, следовательно, 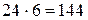 человека.
человека.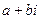 , где
, где  и
и  - вещественные числа, называются комплексными числами.
- вещественные числа, называются комплексными числами.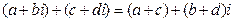 .
.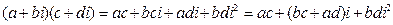 .
.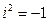 , то получим
, то получим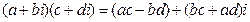 .
.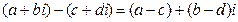 .
.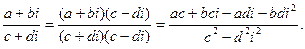
 , то
, то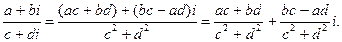
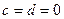 , но в этом случае делитель
, но в этом случае делитель 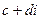 тоже равен нулю. Следовательно, невозможно лишь деление на нуль, что соответствует обычным правилам действий с числами.
тоже равен нулю. Следовательно, невозможно лишь деление на нуль, что соответствует обычным правилам действий с числами. , что
, что 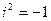 . А, может быть, его на самом деле нет? Чтобы исправить это упущение, используем для построения комплексных чисел уже существующее множество.
. А, может быть, его на самом деле нет? Чтобы исправить это упущение, используем для построения комплексных чисел уже существующее множество.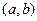 , где вместо запятой стоит «+», а второй элемент пары выделяется умножением на букву
, где вместо запятой стоит «+», а второй элемент пары выделяется умножением на букву 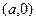 , числу
, числу 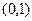 , сложение, вычитание, умножение и деление пар чисел и комплексных чисел происходят по одинаковым правилам. Таким образом, комплексные числа стали реально существующим множеством.
, сложение, вычитание, умножение и деление пар чисел и комплексных чисел происходят по одинаковым правилам. Таким образом, комплексные числа стали реально существующим множеством. , введенная в начале раздела. Причем принято считать, что
, введенная в начале раздела. Причем принято считать, что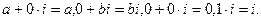
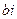 – мнимыми числами. Если
– мнимыми числами. Если  , то число
, то число 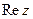 , число
, число 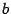 называется мнимой частью и обозначается
называется мнимой частью и обозначается 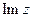 . Число
. Число 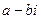 называется сопряженным числу
называется сопряженным числу  и обозначается
и обозначается 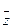 , то есть
, то есть 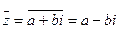 .
.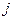 .
.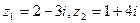 . Тогда:
. Тогда: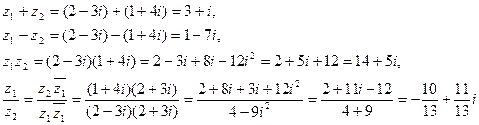
 :
: 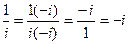 .
.


