
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7.5. Объемы тел и площади их поверхностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Понятие об объеме тела. Отношение объемов подобных тел. Формулы объема куба, параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы. Объем тела – это положительная величина той части пространства, которую занимает геометрическое тело. Объемы равных тел равны. Если тело разбито на несколько тел, не имеющих общих внутренних точек, то его объем равен сумме объемов этих тел. Отношение объемов подобных тел равно кубу коэффициента подобия. Правило. Площадь боковой поверхности призмы равна произведению периметра основания и высоты
Правило. Объем прямой призмы равен произведению площади основания на длины бокового ребра
где
Объем куба равен кубу длины его грани. Формула объема куба
где Объем призмы
Формула объема призмы
где
Объем параллелепипеда Объем параллелепипеда равен произведению площади основания на высоту.
Объем прямоугольного параллелепипеда Объем прямоугольного параллелепипеда равен произведению его Формула объема прямоугольного параллелепипеда
где
Объем цилиндра Объем цилиндра равен произведению площади его основания на высоту.
Объем частей шара Шаровым сегментом называется часть шара, отсеченная от него плоскостью. Если
Шаровой сектор состоит из шарового сегмента и конуса. Поэтому его объем является суммой объемов шарового сегмента
где
Объем шарового сектора
Площадь сферы
Объём шара, ограниченного сферой
Площадь сегмента сферы
где
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1849; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.197.120 (0.01 с.) |

 , где
, где  – площадь боковой поверхности;
– площадь боковой поверхности; – периметр основания призмы (многоугольника, лежащего в основании);
– периметр основания призмы (многоугольника, лежащего в основании); – высота призмы (для прямоугольной — это длина бокового ребра призмы).
– высота призмы (для прямоугольной — это длина бокового ребра призмы). ,
, – объем призмы;
– объем призмы; – длина бокового ребра призмы.
– длина бокового ребра призмы. Объем куба
Объем куба ,
, – длина грани куба.
– длина грани куба. Объем призмы равен произведению площади основания призмы, на высоту.
Объем призмы равен произведению площади основания призмы, на высоту. ,
, – площадь основания призмы,
– площадь основания призмы, Формула объема параллелепипеда
Формула объема параллелепипеда длины, ширины и высоты.
длины, ширины и высоты. ,
, – ширина,
– ширина,  Формулы объема цилиндра
Формулы объема цилиндра ,
,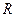 – радиус цилиндра,
– радиус цилиндра, = 3.141592
= 3.141592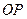 – радиус шара, перпендикулярный отсекающей плоскости, то точку
– радиус шара, перпендикулярный отсекающей плоскости, то точку  назовем в этом случае полюсом шара. Высотой шарового сегмента называется отрезок
назовем в этом случае полюсом шара. Высотой шарового сегмента называется отрезок  , соединяющий полюс шара с центром основания шарового сегмента.
, соединяющий полюс шара с центром основания шарового сегмента. и конуса
и конуса  . Высота
. Высота  шарового сегмента является также высотой и шарового сектора. Имеем
шарового сегмента является также высотой и шарового сектора. Имеем
 ,
, – радиус конуса. Пусть
– радиус конуса. Пусть  – полюса шара,
– полюса шара,  . Из прямоугольного треугольника
. Из прямоугольного треугольника 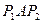 находим
находим  , следовательно,
, следовательно,

 .
. .
. ,
, – высота сегмента, а
– высота сегмента, а  – зенитный угол.
– зенитный угол.


