
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тригонометрические тождества.Содержание книги
Поиск на нашем сайте
Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Это соотношение называется основным тригонометрическим тождеством. Если это уравнение поделить на квадрат косинуса и синуса соответственно имеем далее: Из определений тангенса и котангенса имеем, что Формулами приведения называются формулы следующего вида:
Здесь
Правила преобразования: 1) Если аргумент содержит 2) Определяем знак («+» или «–») значения первоначальной функции. Преобразованное выражение сохраняет знак своего родителя. Формулы сложения Значения тригонометрических функций суммы и разности двух углов:
Формулы для кратных углов Формулы двойного угла:
Формулы половинного угла:
Произведения Формулы для произведений функций двух углов:
Суммы
Обратные тригонометрические функции и их свойства. Арксинус, арккосинус, арктангенс, арккотангенс. Функция 1. 2. 3. 4. функция нечетная, то есть 5. 6. 7. 8. 9. Функция 1. 2. 3. 4. функция ни четная, ни нечетная, причем 5. 6. 7. 8. Функция 1. 2. 3. 4. функция нечетная, то есть 5. 6. 7. 8. график функции имеет 2 асимптоты: Функция 1. 2. 3. 4. функция ни четная, ни нечетная, причем 5. 6. 7. график функции имеет 2 асимптоты:
Тема 2.2 Обратные тригонометрические функции. Тригонометрические уравнения и неравенства Простейшие тригонометрические уравнения. Решения тригонометрических уравнений. Простейшие тригонометрические неравенства. Арксинус, арккосинус, арктангенс, арккотангенс числа.
Тригонометрические уравнения Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим. Простейшие тригонометрические уравнения.
Методы решения тригонометрических уравнений Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида и решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения тригонометрических уравнений. 1. Алгебраический метод. Этот метод нам хорошо известен из алгебры (метод замены переменной и подстановки). Пример. Решить уравнение: Решение. Используя формулы приведения, имеем: 1) 2) 2. Разложение на множители. Этот метод рассмотрим на примерах. Пример. Решить уравнение: Решение. Перенесём все члены уравнения влево: преобразуем и разложим на множители выражение в левой части уравнения:
1) 2) Пример. Решить уравнение: Решение.
2) Пример. Решить уравнение: Решение.
3. Приведение к однородному уравнению. Уравнение называется однородным относительно а) перенести все его члены в левую часть; б) вынести все общие множители за скобки; в) приравнять все множители и скобки нулю; г) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на д) решить полученное алгебраическое уравнение относительно Пример. Решить уравнение: Решение.
корни этого уравнения: 1) 2) 4. Переход к половинному углу. Рассмотрим этот метод на примере: Пример. Решить уравнение: Решение.
.......... 5. Введение вспомогательного угла. Рассмотрим уравнение вида:
Где
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль (абсолютное значение) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как
Пример. Решить уравнение: Решение. Здесь
6. Преобразование произведения в сумму. Здесь используются соответствующие формулы. Пример. Решить уравнение: Решение. Преобразуем левую часть в сумму:
8. Универсальная подстановка. Рассмотрим этот метод на примере. Пример. Решить уравнение: Решение. Здесь возможны два случая: 1)
а) б) 2) Таким образом, решение даёт только первый случай
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 949; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |

 .
. и
и 
 .
.



 – любая тригонометрическая функция,
– любая тригонометрическая функция,  – соответствующая ей кофункция (то есть косинус для синуса, синус для косинуса, тангенс для котангенса, котангенс для тангенса, секанс для косеканса и косеканс для секанса), n – целое число. Перед полученной функцией ставится тот знак, который имеет исходная функция в заданной координатной четверти при условии, что угол α острый, например:
– соответствующая ей кофункция (то есть косинус для синуса, синус для косинуса, тангенс для котангенса, котангенс для тангенса, секанс для косеканса и косеканс для секанса), n – целое число. Перед полученной функцией ставится тот знак, который имеет исходная функция в заданной координатной четверти при условии, что угол α острый, например: .
. где
где  – нечетное натуральное число
– нечетное натуральное число  , то функция меняется на «конфункцию», т.е. синус на косинус, тангенс на котангенс и наоборот. Если
, то функция меняется на «конфункцию», т.е. синус на косинус, тангенс на котангенс и наоборот. Если  , то название функции не изменяется.
, то название функции не изменяется.

















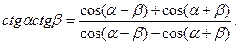





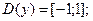



 при
при  ;
; при
при  ;
; при
при  ;
;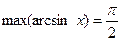 при
при  ;
; при
при  .
.
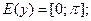

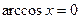 при
при  ;
; при
при  ;
; при
при  при
при  .
.




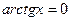 при
при  при
при  ;
; при
при  ;
;
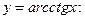


 ни при каких
ни при каких  ;
; при
при  ;
;

 любое целое число;
любое целое число; любое целое число;
любое целое число; любое целое число;
любое целое число; здесь нет решений;
здесь нет решений; - любое целое число.
- любое целое число.
 любое целое число;
любое целое число; любое целое число;
любое целое число; любое целое число;
любое целое число; здесь нет решений
здесь нет решений - любое целое число.
- любое целое число.
 – любое целое число;
– любое целое число; - любое целое число.
- любое целое число.
 - любое целое число;
- любое целое число; - любое целое число.
- любое целое число.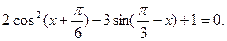
 Делаем замену:
Делаем замену:  тогда
тогда  Находим корни:
Находим корни:  откуда следует два случая:
откуда следует два случая:

 .
. ,
,




 .
. ,
,








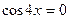 ,
, 
 ,
, 
 ,
, 
 и
и  , если все его члены одной и той же степени относительно
, если все его члены одной и той же степени относительно  .
. .
.

 , отсюда
, отсюда  ,
, отсюда
отсюда
 .
. .
.



 – коэффициенты;
– коэффициенты;  – неизвестное. Разделим обе части этого уравнения на
– неизвестное. Разделим обе части этого уравнения на  :
: .
. и
и  (здесь
(здесь  - так называемый вспомогательный угол), и наше уравнение принимает вид:
- так называемый вспомогательный угол), и наше уравнение принимает вид: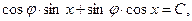 или
или  и его решение:
и его решение:  , где
, где  . Заметим, что введенные обозначения
. Заметим, что введенные обозначения  и
и 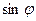 взаимно заменяемы.
взаимно заменяемы.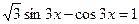 .
. , поэтому делим обе части на
, поэтому делим обе части на 

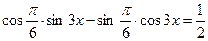 ,
,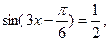 отсюда
отсюда 
 .
.




 , тогда
, тогда 
 ,
,  . Делаем замену:
. Делаем замену:  , тогда
, тогда  , корни этого уравнения:
, корни этого уравнения:  :
:

 , тогда
, тогда  .
.


