
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема (об отрезках хорды).Содержание книги
Поиск на нашем сайте
Пусть точка Иными словами, если через какую-то точку внутри круга провести две хорды, то произведение отрезков, на которые разделилась одна хорда, равно произведению отрезков для другой хорды.
Окружность называется описанной около многоугольника, если она проходит через все его вершины. При этом многоугольник называется вписанным в окружность. Свойство описанного четырехугольника: В
Следствие: В параллелограмм можно вписать окружность тогда и только тогда, когда этот параллелограмм – ромб.
Признак вписанного четырехугольника. Если сумма двух противоположных углов четырехугольника равна 180°, то около этого четырехугольника можно описать окружность (без доказательства). Замечание: Признак вписанного четырехугольника можно переформулировать следующим образом: если суммы противоположных углов четырехугольника равны, то около него можно описать окружность. Следствие: Около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником. Геометрическое место точек (сокращенно ГМТ), обладающих некоторым свойством,- это фигура, состоящая из всех точек, для которых выполнено это свойство. Решение задачи на поиск ГМТ должно содержать доказательство того, что а) точки, обладающие требуемым свойством, принадлежат фигуре F, являющейся ответом задачи; б) все точки фигуры F обладают требуемым свойством. Геометрические преобразования. Геометрическое преобразование плоскости – взаимно-однозначное отображение этой плоскости на себя. Наиболее важными геометрическими преобразованиями являются движения, т.е. преобразования, сохраняющие расстояние. Иначе говоря, если Теорема Менелая. Если прямая пересекает стороны или продолжения сторон
Теорема Чевы. Пусть на сторонах
Парабола – эта линия, которая в некоторой прямоугольной декартовой системе координат Указанная система координат называется канонической, уравнение – каноническим уравнением параболы. Теорема. Парабола представляет собой множество точек, равноудаленных от данной прямой (директрисы параболы) и данной точки (фокуса параболы), не лежащей на директрисе. Эллипс – это линия, которая в некоторой прямоугольной декартовой системе координат Указанная система координат называется канонической, уравнение – каноническим уравнением эллипса. Гипербола – эта линия, которая в некоторой прямоугольной декартовой системе координат Указанная система координат называется канонической, уравнение – каноническим уравнением гиперболы.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 741; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.118 (0.01 с.) |

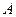 расположена внутри круга радиуса
расположена внутри круга радиуса 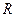 на расстоянии
на расстоянии  от его центра,
от его центра,  - произвольная хорда, проходящая через
- произвольная хорда, проходящая через 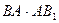 постоянно и
постоянно и 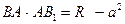 .
. Теорема о сумме квадратов сторон и диагоналей параллелограмма.
Теорема о сумме квадратов сторон и диагоналей параллелограмма. 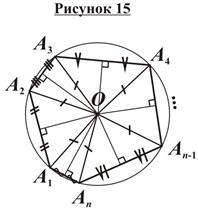 Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.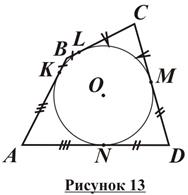 описанном четырехугольнике суммы противоположных сторон равны (рисунок).
описанном четырехугольнике суммы противоположных сторон равны (рисунок).
 Свойство вписанного четырехугольника. Сумма противоположных углов вписанного четырехугольника равна 180°.
Свойство вписанного четырехугольника. Сумма противоположных углов вписанного четырехугольника равна 180°.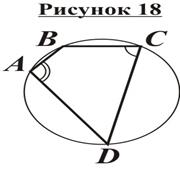
 – движение плоскости, то для любых двух точек
– движение плоскости, то для любых двух точек 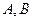 этой плоскости расстояние между точками
этой плоскости расстояние между точками  и
и 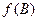 равно
равно 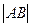 .
.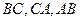 треугольника
треугольника 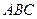 соответственно в точках
соответственно в точках 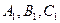 , то имеет место равенство
, то имеет место равенство 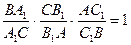 .
.
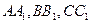 пересекаются в одной точке или
пересекаются в одной точке или 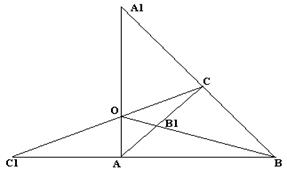 параллельны тогда и только тогда, когда
параллельны тогда и только тогда, когда 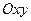 координат имеет уравнение
координат имеет уравнение 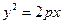 .
.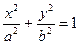 .
.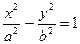 .
.


