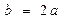Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 5. Уравнения и неравенстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Тема 5.1. Уравнения и неравенства Решение рациональных, показательных, логарифмических уравнений и неравенств. Решение иррациональных уравнений. Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение простейших систем уравнений с двумя неизвестными. Решение систем неравенств с одной переменной. Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
Уравнение вида Например, Решение рациональных уравнений При решении рациональных уравнений необходимо: 1) Обязательно учесть область определения уравнения. 2) Дробь превращается в ноль, когда числитель равен нулю. Пример. Решить уравнение
Ответ. Область определения необходимо находить до преобразования и возможного сокращения дробей. Показательные уравнения Показательные уравнения – уравнения, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения вида Примеры решений показательных уравнений: 1. Решить уравнение Так как Ответ: 2. Решить уравнение Заменой Ответ: 1. Решить уравнение Используем, что 32х·34 - 11·32х = 210 32х(34 - 11) = 210 70·32х = 210 32х = 3 32х = 31
Логарифмическое уравнение. Определение. Логарифмическое уравнение – это уравнение вида Уравнения, сводящиеся к этому виду, также называются логарифмическими уравнениями. Правило: логарифмическое уравнение Пояснение: В процессе решения логарифмического уравнения Важно знать: 1) Если в уравнении разные основания, то логарифмы убирать нельзя. В левой и правой частях уравнения должны быть одинаковые основания. Возьмем для примера уравнение:
Здесь слева и справа одинаковое основание 5. Значит, можно убрать значки логарифмов и привести уравнение к более простому и понятному виду:
Если основания неодинаковы, необходимо преобразовать одно из выражений так, чтобы основания стали одинаковыми – и только после этого уравнение можно потенцировать. 2) Даже если основания слева и справа одинаковые, но в уравнении есть коэффициент, то в этом случае тоже убирать логарифмы нельзя. К примеру, нельзя потенцировать уравнение такого типа:
Мешает коэффициент 3 в левой части. Поэтому уравнение надо преобразовать так, чтобы коэффициент исчез. В нашем уравнении, применив одно из свойств логарифмов
Тогда наше уравнение обретает другой вид:
Теперь мы имеем одинаковые основания (число 2), и уравнение без коэффициентов. Значит, уже легко можем убрать значки логарифмов:
И такое уравнение решать намного проще:
3) Даже при одинаковых основаниях и отсутствии коэффициентов нельзя потенцировать уравнение, если в какой – то из его частей больше одного логарифма. Например, нельзя убирать логарифмы в уравнении
В левой части два логарифма. Надо сначала преобразовать ее. Для этого воспользуемся еще одним правилом: сумма логарифмов равна логарифму произведения. Итак, преобразовываем левую часть уравнения:
У нас получилось выражение с одним логарифмом. А наше уравнение принимает новый вид:
И мы уже можем убрать значки логарифмов:
Решаем это простое уравнение:
Пример. Решим уравнение
Решение. 1) Поскольку основания в левой и правой частях одинаковые (равны 3), то мы можем освободиться от знаков логарифмов и прийти к уравнению вида 2) Приравниваем уравнение к нулю и получаем квадратное уравнение:
Решив квадратное уравнение, находим его корни:
3) Проверим, при каком из двух значений Мы уже знаем, что логарифмическое уравнение равносильно уравнению
При При Логарифмическое неравенство. Определение: логарифмическое неравенство – это неравенство вида
Неравенства, сводящиеся к этому виду, также называются логарифмическими неравенствами. Правило: если - при - при Пример. Решим неравенство Решение. 1) В основании обеих частей уравнения – одно и то же число 3. Значит, можем убрать значки логарифмов. Поскольку 3>1, то, следуя правилу, составляем следующую систему неравенств: Решаем неравенства и получаем: Мы видим, что Уравнения, в которых переменная содержится под знаком корня, называются иррациональными. Решение иррациональных уравнений сводится к переходу от иррационального к рациональному путем возведения в степень обеих частей уравнения или замены переменной. При решении иррациональных уравнений после получения корней лучше всегда делать проверку! Пример. Решить уравнение
Проверка: Ответ. При решении иррационального уравнения вида Пример. Решить уравнение Решение. При
Отсюда Ответ. Систему двух уравнений с двумя переменными обозначают двумя скобками и обычно записывают в виде:
Несколько уравнений с двумя (или более) переменными образуют систему уравнений, если ставится задача найти множество общих решений этих уравнений:
Множество упорядоченных пар, троек (в случае систем с тремя переменными) и т.д. значений переменных, обращающих в истинное равенство каждое уравнение системы, называется решением системы уравнений. Решить систему уравнений – значит найти все ее решения или доказать, что решений нет. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Система уравнений называется определенной, если она имеет конечное число решений, и неопределенной, если она имеет бесчисленное множество решений. Две системы называются равносильными, если они имеют одно и то же множество решений. Система уравнений называется линейной, если все уравнения, входящие в систему, являются линейными. Если система из n линейных уравнений содержит n неизвестных, то возможны следующие три случая: 1) система не имеет решений; 2) система имеет одно решение; 3) система имеет бесконечное множество решений. Основными методами решения систем уравнений являются следующие: 1) метод подстановки; 2) метод алгебраического сложения (или метод преобразования системы); 3) метод замены переменных; 4) графический метод. При решении системы методом подстановки сначала из какого-нибудь уравнения выражают одну переменную через другую. Полученное выражение подставляют в другое уравнение системы, в результате чего приходят к уравнению с одной переменной, затем решают это уравнение и находят соответствующее значение второй переменной. При решении системы методом алгебраического сложения переходят от данной системы к равносильной ей, в которой одно из уравнений содержит только одну переменную. При этом обычно умножают одно или оба уравнения на числовые множители таким образом, чтобы коэффициенты при x или y были одинаковыми, но с противоположными знаками. Пример. Решить систему уравнений Решение. Решим исходную систему двумя способами: методом подстановки и методом алгебраического сложения. 1 способ (метод подстановки).
Из уравнения (а) Итак, получаем 2 способ (метод алгебраического сложения). Решая этим способом, умножим первое уравнение системы на 3, а второе на (– 2), и сложим:
4) Система двух уравнений, из которых одно первой степени, а другое второй. Пусть дана система:
Всего удобнее такую систему решить способом подстановки следующим путем, Из уравнения 1-й степени определяем одно какое-нибудь неизвестное, как функцию от другого неизвестного, напр., определяем у, как функцию от
Тогда уравнение 2-й степени после подстановки дает уравнение с одним неизвестным
После этого из уравнения у = 2 х — 1 находим:
Таким образом, данная система имеет две пары решений:
Подобным путем всегда можно решить систему двух уравнений, если одно уравнение первой степени, а другое — второй. Так, напр., легко решается система:
Впрочем, эту систему можно решить весьма просто иначе. Так как уравнения дают сумму и произведение неизвестных, то эти неизвестные можно рассматривать как корни такого приведенного квадратного уравнения, у которого коэффициент при Один корень этого уравнения можно принять за Рассмотрим аналитический способ решения систем алгебраических уравнений. Решим систему уравнений: Умножим второе уравнение на 2 и сначала сложим с первым, а затем вычтем из первого. Получим: Задача сводится к системе линейных уравнений с двумя неизвестными: Применяя к полученным системам метод сложения (т.е. сперва сложим эти уравнения, а далее вычтем из первых – вторые), получим: Рассмотрим еще один пример решения системы уравнений Если применить метод подстановки, т.е. подставить в первое уравнение значение переменной или в каноническом виде: Корни последнего уравнения нетрудно найти: Откуда, путем обратной подстановки в выражение Итак, ответ: При построении математической модели текстовой задачи принято неизвестную величину обозначать какой-либо переменной (обычно х) и по условию задачи составлять равенство. Таким образом поступали математики еще с древних времен, а полученное равенство стали называть уравнением. Однако уравнения появляются и в других задачах, например, в задачах про «задуманное число», при нахождении неизвестных компонент действий и т.п. Поэтому в математике термин «уравнение» используется в более широком смысле. Решить уравнение на языке математики означает найти его корни, то есть все числа, обращающие уравнение в числовое равенство. В школьном курсе математики рассматриваются различные уравнения: иррациональные, показательные, логарифмические, тригонометрические. Алгебраическим уравнением называется уравнение Решение уравнения второй степени обычно не представляет сложности. Уравнения вида Однако, во многих случаях замена переменной не так очевидна, а иногда приходится использовать несколько видов замен переменной. Например, рассмотрим уравнение Доказательства неравенств. Неравенство о среднем арифметическом и среднем геометрическом двух чисел. С необходимостью сравнивать какие-то величины мы сталкиваемся постоянно. При сравнении чисел a и b принято результат сравнения записывать в виде равенства или неравенства. Для произвольных величин a и b выполняется одно и только одно из соотношений a = b, a < b или a > b. В зависимости от конкретного вида чисел используется тот или иной способ сравнения. Однако удобно применять такой способ сравнения величин, который охватывал бы все случаи. Он заключается в том, что составляют разность сравниваемых величин и выясняют, является ли она положительной, отрицательной или нулем. Данный способ сравнения чисел основан на следующем определении: число a больше числа b, если разность a – b – положительное число. Данное определение широко используется при решении различных задач. Пусть a и b – положительные числа. Средним арифметическим двух чисел a и b называется число Для доказательства второй части неравенства рассмотрим разность
При a > 0, b > 0 полученная разность отрицательна или равна нулю и, следовательно, верно неравенство Итак, для двух чисел a > 0, b > 0 выполнено неравенство, связывающее среднее арифметическое, среднее геометрическое и среднее гармоническое этих чисел. Рассмотрим графический способ решения систем алгебраических уравнений. Пусть надо решить систему уравнений: Графический способ. Построим в одной координатной плоскости графики функций
Рассмотрим еще один пример решения системы уравнений графическим способ. Пусть надо решить систему уравнений: Построим в одной координатной плоскости графики функций Метод интервалов В основе этого метода лежит следующее свойство двучлена Пусть требуется решить неравенство Рассмотрим функцию На этом рассуждении и основан метод интервалов, состоящий в следующем: на числовую ось наносят числа Тогда множеством всех решений неравенства Метод интервалов можно применять и при решении неравенств вида
Пример. Решить неравенство Решение. Перепишем неравенство в виде Ответ. (− Пусть требуется решить неравенство Рассмотрим свойство двучлена · если · если Рассмотрим функцию Для любого числа Таким образом, на числовую ось наносят числа Пример. Решить неравенство методом интервалов Решение. Функция
–2 –1 4 На рисунке отмечен знак функции Ответ.
В совершенно различных, на первый взгляд, задачах можно обнаружить, что их решение практически одинаково. Например, если на столе лежат 2 яблока, 2 апельсина и груша, то общее количество фруктов находится как сумма 2+2+1=5. Но точно так же можно определить и число уроков во вторник, зная, что по расписанию будет два урока русского языка, две математики и физкультура. В этих двух задачах используется одна и та же математическая модель, т.к. складываются не фрукты или уроки, а натуральные числа. Математической моделью называют способ описания реальной жизненной ситуации (задачи) с помощью математического языка. Рассмотрим такую ситуацию: в школе четыре седьмых класса. В 7А учатся 15 девочек и 13 мальчиков, в 7Б – 12 девочек и 12 мальчиков, в 7В – 9 девочек и 18 мальчиков, в 7Г – 20 девочек и 10 мальчиков. Если нам нужно ответить на вопрос, сколько учеников в каждом из седьмых классов, то нам 4 раза придется осуществлять одну и ту же операцию сложения: в 7А 15 + 13 = 28 учеников; в 7Б 12 +12 = 24 ученика; в 7В 9 + 18 = 27 учеников; в 7Г 20 + 10 = 30 учеников. Используя математический язык, можно все эти четыре разные ситуации объединить: в классе учатся а девочек и В следующей таблице приведены различные реальные ситуации и их математические модели; при этом а – число девочек в классе, b – число мальчиков в том же классе.
Составляя эту таблицу, мы шли от реальной ситуации к ее математической модели. Не надо уметь двигаться и в обратном направлении, т.е. по заданной математической модели описывать словами реальную ситуацию. Например, что означает (при тех же обозначениях, что и в нашей таблице) такая математическая модель: а – 5 = 6 + 5? Она означает, что если из класса уйдут 5 девочек и придут 5 мальчиков, то девочек и мальчиков в классе станет поровну (эта ситуация имеет место в 7Г из рассмотренного примера). Наверное, у вас возник вопрос: а зачем нужна математическая моде
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 10623; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |

 , где
, где  – многочлены, называется рациональным.
– многочлены, называется рациональным. . Подобное уравнение
. Подобное уравнение  возможно привести к рациональному, преобразовав его.
возможно привести к рациональному, преобразовав его.

 - исключаем, так как не входить в область определения.
- исключаем, так как не входить в область определения. .
. , где
, где  – неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием
– неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием  равны только тогда, когда равны их показатели.
равны только тогда, когда равны их показатели. .
. , то уравнение можно записать в виде
, то уравнение можно записать в виде  , откуда
, откуда  .
. .
. данное уравнение сводится к квадратному уравнению
данное уравнение сводится к квадратному уравнению  . Решая это уравнение, находим его корни:
. Решая это уравнение, находим его корни:  , откуда
, откуда  . Уравнение
. Уравнение  имеет корень
имеет корень  , а уравнение
, а уравнение  не имеет корней, так как показательная функция не может принимать отрицательные значения.
не имеет корней, так как показательная функция не может принимать отрицательные значения. .
. и
и 
 .
. где
где  , если
, если  и
и  .
. .
. .
. .
. мы можем преобразовать выражение слева:
мы можем преобразовать выражение слева: .
. .
. .
. ;
;  ;
;  ;
;  .
. .
.
 .
. .
. ;
;  ;
;  .
. .
. :
:  .
. ;
;  .
. .
. уравнение имеет смысл.
уравнение имеет смысл. и
и  ;
;  .
. неравенства неверны. Значит, 4 не является решением уравнения.
неравенства неверны. Значит, 4 не является решением уравнения. неравенства верны. Значит, 3 является единственным решением уравнения.
неравенства верны. Значит, 3 является единственным решением уравнения. , где
, где  логарифмическое неравенство
логарифмическое неравенство  ;
; 0 логарифмическое неравенство
0 логарифмическое неравенство  .
. .
.

 мы уже в расчет не берем: если
мы уже в расчет не берем: если  .
. .
.


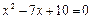

 .
.  - не является корнем.
- не является корнем. .
. можно использовать следующее правило
можно использовать следующее правило  .
. .
. переходим к равносильному уравнению
переходим к равносильному уравнению  . При
. При  обе части уравнения возводим в квадрат. Получаем
обе части уравнения возводим в квадрат. Получаем
 (допустимый корень), а
(допустимый корень), а  не удовлетворяет условию
не удовлетворяет условию  .
. .
. .
. .
. .
. . Подставляя в уравнение (б), получаем:
. Подставляя в уравнение (б), получаем:  .
. .
. ,
, . То есть
. То есть  .
. .
.

 .
. .
. :
:  .
.

 или
или 
 то есть
то есть 


 .
.
 , выраженное через
, выраженное через  , после некоторых упрощений получим биквадратное уравнение:
, после некоторых упрощений получим биквадратное уравнение: ,
, .
. .
. значений
значений  .
. .
. , где
, где  – некоторый многочлен. Если
– некоторый многочлен. Если  называются биквадратными и решаются при помощи подстановки
называются биквадратными и решаются при помощи подстановки  . После этой подстановки уравнение сводится к квадратному и его дальнейшее решение обычно не вызывает затруднений.
. После этой подстановки уравнение сводится к квадратному и его дальнейшее решение обычно не вызывает затруднений. , при условии
, при условии  . В данном уравнении полагаем
. В данном уравнении полагаем  . После умножения первой скобки на вторую и третьей на четвертую имеем
. После умножения первой скобки на вторую и третьей на четвертую имеем  . После выделения полного квадрата в каждой из полученных скобок делаем замену
. После выделения полного квадрата в каждой из полученных скобок делаем замену  , получая уравнение
, получая уравнение  , которое после преобразований приводим к квадратному
, которое после преобразований приводим к квадратному  и решаем относительно переменной y.
и решаем относительно переменной y. , средним геометрическим – число
, средним геометрическим – число  , средним гармоническим – число
, средним гармоническим – число  . Докажем, что эти величины связаны следующим соотношением:
. Докажем, что эти величины связаны следующим соотношением:  . Рассмотрим следующую разность
. Рассмотрим следующую разность  . При a > 0, b > 0 полученная разность неотрицательна и, следовательно, верно неравенство
. При a > 0, b > 0 полученная разность неотрицательна и, следовательно, верно неравенство  .
. .
. .
. .
. и
и  (рис.3). Эти графики пересекаются в четырех точках. Абсциссы и ординаты точек пересечения являются корнями данной системы уравнений. Из рис.3 видно, что значения корней следующие:
(рис.3). Эти графики пересекаются в четырех точках. Абсциссы и ординаты точек пересечения являются корнями данной системы уравнений. Из рис.3 видно, что значения корней следующие:  .
.

 и
и  : точка
: точка  делит числовую ось на две части – справа точки
делит числовую ось на две части – справа точки  двучлен
двучлен  , где
, где  – фиксированные числа, среди которых нет равных, причем такие, что
– фиксированные числа, среди которых нет равных, причем такие, что  .
. . Для любого числа
. Для любого числа  такого, что
такого, что  , соответствующее числовое значение любого сомножителя в произведении положительно, а значит,
, соответствующее числовое значение любого сомножителя в произведении положительно, а значит,  . Для любого числа
. Для любого числа  , взятого из интервала
, взятого из интервала  , соответствующее числовое значение любого из множителей, кроме множителя
, соответствующее числовое значение любого из множителей, кроме множителя  , положительно, поэтому число
, положительно, поэтому число  и т.д.
и т.д.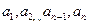 ; в промежутке справа от наибольшего из них, т. е. числа
; в промежутке справа от наибольшего из них, т. е. числа  , ставят знак плюс, а в следующем за ним справа налево интервале ставят знак минус, затем – знак плюс, затем – знак минус и т. д.
, ставят знак плюс, а в следующем за ним справа налево интервале ставят знак минус, затем – знак плюс, затем – знак минус и т. д. будет объединение всех промежутков, в которых стоит знак минус.
будет объединение всех промежутков, в которых стоит знак минус. , где
, где  и
и  функции, так как это неравенство равносильно неравенству
функции, так как это неравенство равносильно неравенству 
 .
. . Отметим на координатной оси числа –3, –2,5 и 4. Определим знаки на промежутках и расставим знаки плюс и минус так, как указано на рисунке. Решениями неравенства будут все
. Отметим на координатной оси числа –3, –2,5 и 4. Определим знаки на промежутках и расставим знаки плюс и минус так, как указано на рисунке. Решениями неравенства будут все  из объединения промежутков (−
из объединения промежутков (−  ;−3) и (-2,5; 4).
;−3) и (-2,5; 4). (−2
(−2  5;4)
5;4) , где
, где  – целые положительные числа;
– целые положительные числа;  – действительные числа, среди которых нет равных, причем такие, что
– действительные числа, среди которых нет равных, причем такие, что  .
. . Точка
. Точка  делит числовую ось на две части, причем:
делит числовую ось на две части, причем: четное, то выражение
четное, то выражение  справа и слева от точки
справа и слева от точки  сохраняет положительный знак;
сохраняет положительный знак; нечетное, то выражение
нечетное, то выражение 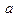 положительно, а слева от точки
положительно, а слева от точки  , где a 1 < a 2 <..< an - 1 < a n.
, где a 1 < a 2 <..< an - 1 < a n. такого, что
такого, что  , соответствующее числовое значение любого сомножителя в произведении положительно, а значит
, соответствующее числовое значение любого сомножителя в произведении положительно, а значит  . Для любого числа x 1, взятого из интервала
. Для любого числа x 1, взятого из интервала  , соответствующее числовое значение любого из множителей, кроме множителя
, соответствующее числовое значение любого из множителей, кроме множителя  , положительно, если
, положительно, если  – четное число, и отрицательно, если
– четное число, и отрицательно, если  , если
, если  , если
, если  на любом интервале.
на любом интервале. . В промежутке справа от наибольшего из них, т. е. числа
. В промежутке справа от наибольшего из них, т. е. числа  , ставят знак плюс, а затем, двигаясь, справа налево, при переходе через очередное число меняют знак, если
, ставят знак плюс, а затем, двигаясь, справа налево, при переходе через очередное число меняют знак, если  .
. непрерывна в каждой точке своей области определения (это дробно – рациональная функция) и обращается в нуль в точке
непрерывна в каждой точке своей области определения (это дробно – рациональная функция) и обращается в нуль в точке  . Область определения этой функции – вся числовая прямая, за исключением нулей знаменателя, то есть точек –2 и 4. Эти три точки
. Область определения этой функции – вся числовая прямая, за исключением нулей знаменателя, то есть точек –2 и 4. Эти три точки  ,
,  и
и  разбивают область определения функции
разбивают область определения функции  на 4 промежутка, в каждом из которых функция
на 4 промежутка, в каждом из которых функция 


 + – + –
+ – + –
 в каждом из соответствующих интервалов, который определяем, найдя знаки значений функции
в каждом из соответствующих интервалов, который определяем, найдя знаки значений функции  во внутренних точках интервалов. Неравенство нестрогое, поэтому числа –2 и 4 (нули функции
во внутренних точках интервалов. Неравенство нестрогое, поэтому числа –2 и 4 (нули функции  .
. .
. мальчиков, значит, всего учеников
мальчиков, значит, всего учеников  . Эту запись
. Эту запись 
 или
или  или
или 
 или
или  или
или 

 или
или