
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1 Тригонометрические уравнения в школьном курсе математикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Содержание ВВЕДЕНИЕ.. 3 Глава 1 Тригонометрические уравнения в школьном курсе математики. 4 1.1 Роль и место тригонометрических уравнений в школьном курсе математики 4 1.2 Обзор методической литературы.. 6 Глава 2 Методические и технологические аспекты подготовки школьников к сдаче ЕГЭ по математике по теме «Тригонометрические уравнения». 9 2.1 Виды простейших тригонометрических уравнений и методы их решения 9 2.2 Общие методы решения тригонометрических уравнений. 12 Глава 3 Основные типы учебных задач темы и приемы их решения. 32 3.1 Базовые задачи: 32 3.2 Задачи для самостоятельного решения. 37 Глава 4 Характерные затруднения учащихся при решении тригонометрических уравнений и пути их преодоления. 39 Заключение. 46 Литература. 47 Приложение 1. 49
ВВЕДЕНИЕ Тригонометрия является одним из наиболее молодых отделов элементарной математики. На первоначальных стадиях своего развития тригонометрия служила средством решения вычислительных геометрических задач. Ее содержанием считалось вычисление элементов простейших геометрических фигур, то есть треугольников. Но в современной тригонометрии самостоятельное значение имеет изучение тригонометрических функций и их свойств. Этот период развития тригонометрии был подготовлен всем ходом развития механики колебательных движений, физики звуковых, световых и электромагнитных волн. Исторически сложилось, что тригонометрическим уравнениям и неравенствам уделялось особое место в школьном курсе. Еще греки на заре человечества, считали тригонометрию важнейшей из наук. Поэтому и мы, не оспаривая древних греков, будем считать тригонометрию одним из важнейших разделов школьного курса, да и всей математической науки в целом. Решение тригонометрических уравнений создаёт предпосылки для систематизации знаний учащихся, связанных со всем учебным материалом по тригонометрии (например, свойства тригонометрических функций, приёмы преобразования тригонометрических выражений и т.д.) и даёт возможность установить действенные связи с изученным материалом по алгебре (уравнения, равносильность уравнений, неравенства, тождественные преобразования алгебраических выражений и т.д.). Иначе говоря, рассмотрение приёмов решения тригонометрических уравнений предполагает своего рода перенос этих умений на новое содержание. Перед учителем стоит задача – формировать у учащихся умения решать уравнения каждого вида, развивая тем самым общие тригонометрические представления. В процессе разработки методических и технологических аспектов подготовки учащихся к ЕГЭ по теме «Тригонометрические уравнения» необходимо было решить следующие задачи: 1. Провести анализ психолого-педагогической, учебной и методической литературы по проблеме исследования. 2. Выявить роль тригонометрических уравнений в обучении математики. 3. Выделить основы формирования умений необходимых для решения тригонометрических уравнений. 4. Классифицировать методы решения тригонометрических уравнений. 5. Разработать методику формирования умений и навыков решать тригонометрические уравнения. 6. Провести экспериментальное исследование разработанной методики; выделить типичные ошибки учащихся и их причины. 7. Сделать подборку заданий для подготовки учащихся к ЕГЭ.
Глава 1 Тригонометрические уравнения в школьном курсе математики Тригонометрические уравнения, содержащие одну и ту же функцию одного и того же аргумента и решаемые методом подстановки Уравнения данного вида Пример: Решите уравнение:
Пусть
Оба корня уравнения удовлетворяют условию допустимого значения t, следовательно, переходим к обратной замене.
Однородные уравнения Предварительно можно показать учащимся вид однородной функции от двух переменных U и V первой степени, например, 3U + 2V; второй степени: Для лучшего усвоения и закрепления идеи необходимо решить с учащимися следующее уравнение: Обозначим Получается однородное уравнение второй степени:
Имеем 2 случая: U = V или V = 0,5 U
Как правило, на практике очень часто встречается Примеры: 1. Это однородное уравнение первой степени. Обе части уравнения нужно разделить на cosx. При этом получится равносильное уравнение. Чтобы в этом удостовериться, покажем, что уравнение cosx = 0 не содержит корней данного уравнения. Действительно, если
, то
Но это невозможно, т.к. Следовательно, имеем равносильное уравнение
2. Это однородное уравнение второй степени. Получим равносильное уравнение после деления обеих частей уравнения на
При решении уравнений такого типа необходимо пользоваться известным правилом: произведение нескольких множителей равно нулю, если хотя бы один из них равен нулю, а остальные при этом имеют смысл. Примеры: 1.
2. Сгруппировав соответствующие слагаемые, получим:
Один из способов решения такого уравнения состоит в том, что левую часть уравнения можно преобразовать по формуле:
Примеры:
1.
Подставляя в формулу, получаем:
2.
Подставляя в формулу, получаем
К сожалению, внимание учащихся нечасто обращается на преобразование выражения В некоторых пособиях эта формула приведена в таком виде
Такая запись приведёт к ошибке, если, например, a и b отрицательны. Профильный уровень | Репродуктивный | 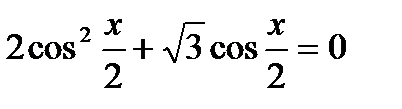
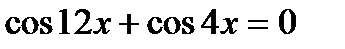
|
| Эвристический | 
| ||
| Исследовательский | |||
| Б4 Однородные уравнения | |||
| Общеобразовательный уровень | Репродуктивный |  
| |
| Эвристический | 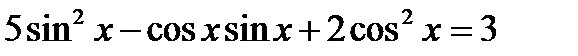
| ||
| Исследовательский | |||
| Профильный уровень | Репродуктивный | 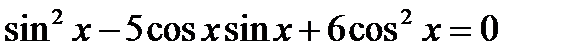
| |
| Эвристический | 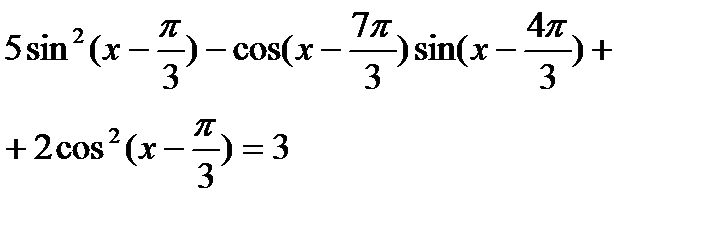
| ||
| Исследовательский |
| . Б5. Уравнения, решаемые понижением степени | |||||||||||||||||||||||||||
| Общеобразовательный уровень | Репродуктивный |   
| |||||||||||||||||||||||||
| Эвристический | 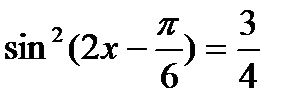
| ||||||||||||||||||||||||||
| Исследовательский | |||||||||||||||||||||||||||
Профильный уровень | Репродуктивный | 
| |||||||||||||||||||||||||
| Эвристический | 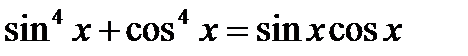
| ||||||||||||||||||||||||||
| Исследовательский | |||||||||||||||||||||||||||
| Б6. Уравнения, решаемые с помощью оценок. | |||||||||||||||||||||||||||
| Репродуктивный | 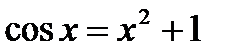
| ||||||||||||||||||||||||||
| Эвристический | 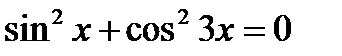
| ||||||||||||||||||||||||||
| Исследовательский | |||||||||||||||||||||||||||
| Репродуктивный | 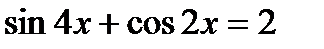
| ||||||||||||||||||||||||||
| Эвристический | 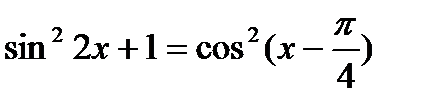
| ||||||||||||||||||||||||||
| Исследовательский | |||||||||||||||||||||||||||
| Б8 Уравнения, решаемые с помощью введения вспомогательного аргумента | ||
| Общеобразовательный | Репродуктивный | 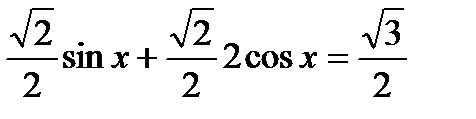
|
| Эвристический | 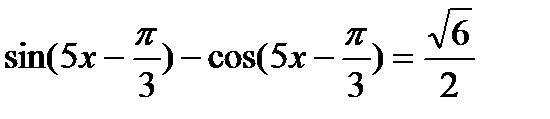
| |
| Исследовательский | 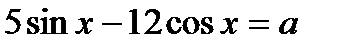
| |
| Профильный уровень | Репродуктивный | 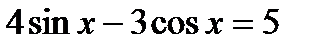
|
| Эвристический | 
| |
| Исследовательский | 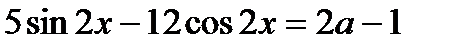
|
3.2 Задачи для самостоятельного решения
Задачи начального уровня
Первую группу тригонометрических уравнений, которые нужно предложить учащимся для самостоятельного решения, составляют тригонометрические уравнения, способ решения которых основан на определениях и некоторых свойствах тригонометрических функций.
1. 2sin4x-1=0
2. cos(-x/2)=√3/2
3. tg(2x-1)=√3
4. 2sin(1-2x/3)=-1
5. ctg(-2x)=-√3∕3
6. sin(П∕2-2x)-2cos(4П-2x)=√2∕2
7. sin(2П-0,5x)+3sin(П-0,5x)=-√2
8. 2cos (3П-x∕4)+3sin(П∕2-x∕4)=0
9. ctg(3П/2+x)-2tg(П+x)=-1
10. 4cos(3П+4x)sin((П-4x)=0
11. cosxtgx=1
12. cosx - sinx=3
13. sin3x=2+sinx
Задачи повышенного уровня
1. Уравнения, сводящиеся к квадратным уравнениям.
1) 2sin2x+sinx-1=0
2) tg3П+2tg2x+3tgx=0
3)8cos2x+6sinx-3=0
2. Уравнения, решаемые разложением на множители.
1) tgx - sinx=1- tgx
2) sin(x+П∕4)=sin3x+cos3x
3)sin2x=cosx
4) 2cosxcos2x=cosx
3. Однородные уравнения и уравнения, приводимые к однородным уравнениям.
1) cos3x +sin3x=0
2) sin5x+cos5x=0
3) 3sin2x-sinxcosx-4cos2x=0
4) 3sin2x+sinxcosx=2cos2x
4. Уравнения, решаемые понижением степени
1) sin 2x+sin24x=sin25x+sin26x
2)sin4x+cos4x=1∕9
3) sin 2x+sin22x=1
5. Уравнения, решаемые с помощью оценок.
1)2cos2x+sin(5x∕2)=3
2) sin 2x+√3sin2x+cos(12x∕5)=5-3cos2x
6. Уравнения, решаемые с помощью введения вспомогательного аргумента.
1) sinx + cosx =√2
2)√3/2cosx+1∕2sinx=1
7. Данная группа задач объединяет тригонометрические уравнения, решение которых потребует выполнения тождественных преобразований тригонометрических и алгебраических выражений для приведения данного уравнения к одному из известных видов и требующие учета ОДЗ. Такие задания вынесены на ЕГЭ во второй части работы, в разделе С1
1.Решите уравнение 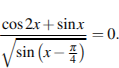
2.Решите уравнение 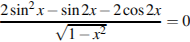
3.Решите уравнение 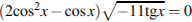
4.Решите уравнение 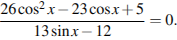
5.Решите уравнение 
6.Решите уравнение 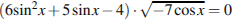
7. а) Решите уравнение 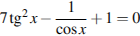 .
.
б) Найдите все корни этого уравнения, принадлежащие промежутку  .
.
Обучающий эксперимент
Целью данного этапа является формирование умений учащихся решать тригонометрические уравнения.
Для реализации поставленной цели сформулированы следующие задачи:
- в соответствии с результатами предыдущего этапа внести коррективы в разработанную методику изучения тригонометрических уравнений, направленную на развитие тригонометрических представлений;
- применять данную систему заданий на уроках и дополнительных занятиях со слабыми учащимися;
- организовать деятельность учащихся на занятиях, направленную на формирование умений решать тригонометрические уравнения.
Для реализации данных задач были проведены уроки и дополнительные занятия. Содержание этих занятий включало в себя теоретическую и практическую часть. Конспект урока (приложение1)
На третьем этапе контроля знаний осуществляется систематизация учебного материала по теме «Решение тригонометрических уравнений». Проконтролировать знания учащихся можно с помощью зачетной работы.
В ней рассматриваются различные методы решения тригонометрических уравнений. Среди этих методов как методы решения, применяемые ко всем видам уравнений (разложение на множители, использование формул корней квадратного уравнения, введение новой переменной и т.д.) так и методы специфические (применение формул понижения степени, формул преобразования суммы тригонометрических выражений в произведение, введение вспомогательного аргумента)
Зачетная работа.
Б4 Однородные уравнения
№1  ; (
; (
№2  ; (
; (
Переход к основной части
Данный этап урока, призван сформировать проблему, решению которой будет посвящена основная часть урока.
| Ученики предполагают, что данное уравнение, возможно, решить с помощь введение вспомогательного угла. Учитель соглашается и предлагает записать решение этого уравнения. На экране по мере того, как ученики говорят этапы алгоритма, появляются соответствующие записи. Учителю только важно изначально направить учеников на формулу косинуса суммы, а также обратить внимание на четность косинуса, которая позволяет упростить конечный вид серии корней. |
Основная часть
После получения серии корней в части 2.1 учитель обращает внимание некоторую «некомпактность» данного ответа и сложности в восприятии этой информации. Например, сложности, которые возникнут, если необходимо будет найти корни на заданном промежутке. Далее учитель сообщает, что одно из замечательных отличий тригонометрических уравнений состоит в том, что в зависимости от избранного метода решения, можно получить разные виды записи одних и тех же корней. Поэтому, возможно, если мы решим данное в 2.1 уравнение каким-то другим способом, вариант записи ответа получится предпочтительнее.
| Ученики записывают ещё раз уравнение. Учитель подсказывает идею об использовании формулы двойного угла. После чего на доске появляются формулы двойного угла. Ученики устно проговаривают, как будут раскрываться двойные углы. После чего на доске появляется преобразования. По ходу ученики говорят о том, что надо раскрыть скобки и привести подобные слагаемые. | |
После того, как уравнение сводится к данному на слайде уравнению, предлагается ученикам определить, какой вид имеет уравнение и как его необходимо решать. Ученики догадываются. Что перед ними однородное уравнение и что его имеет смысл разделить на  (проговаривается, что данное выражение не будет равно 0, так как в противном случае получаем противоречие основному тригонометрическому тождеству). К доске вызывается ученик, который будет оформлять решение, остальные самостоятельно оформляют решение в тетради, а затем проверяют. Возможное решение: (проговаривается, что данное выражение не будет равно 0, так как в противном случае получаем противоречие основному тригонометрическому тождеству). К доске вызывается ученик, который будет оформлять решение, остальные самостоятельно оформляют решение в тетради, а затем проверяют. Возможное решение:

| |
|
| Учитель обращает внимание на то, что второй вариант записи корней выглядит предпочтительнее. Поэтому имеет смысл обобщить опыт решения данного уравнения вторым способом. Ещё раз с учениками проговаривается ход решения, после чего задаётся вопрос: можно ли изначально все тригонометрические функции выразить, через тангенс половинного угла? Ученики должны дать утвердительный ответ и догадаться о применении формул двойного угла для этой процедуры. |
|
| Учитель предлагает оформить процедуру для синуса угла х. На доске по мере того, как озвучивается необходимость того или иного действия, появляется его визуализация. |
К доске вызывается ученик для оформления процедуры сведения косинуса угла х, к тангенсу его половинного угла. Сама запись может выглядеть таким образом:
 | |
Сообщается, что, так как в итоге можно свести все известные тригонометрические функции к функции тангенса половинного угла (тангенс х, сводится по формуле тангенса двойного угла, а котангенс, как взаимообратное к тангенсу), то данные формулы называются формулами универсальной тригонометрической подстановки. Пока ученики их записывают в тетрадь, также сообщается, что после замены тангенса половинного угла на переменную, любое тригонометрическое уравнение фактически можно свести к алгебраическому от одной переменной.
Однако, есть тонкость, которая может привести к ошибке. Дело в том, что полученное уравнение не будет равносильно исходному, если в изначальном уравнении не будет тангенса половинного угла. В этом случае нам необходимо проверять, является ли серия 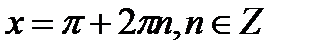 Корнем уравнения. И если да, то должны включить эту серию в ответ. Всё это несколько осложняет использование формул.
Корнем уравнения. И если да, то должны включить эту серию в ответ. Всё это несколько осложняет использование формул.
|
Закрепление материала
Цель данного этапа проверить действие формул на практике. Учитель совместно с учениками на доске оформляет решение. Ученики записывают решение в тетрадь.
Возможное решение первого уравнения:
Очевидно, проверку серии  делать не надо, так как тангенс половинного угла присутствует, и во время замены мы не сузим область допустимых значений. делать не надо, так как тангенс половинного угла присутствует, и во время замены мы не сузим область допустимых значений.
 Критерий равенства произведения 0, проговаривается
Критерий равенства произведения 0, проговаривается
 или или  Второе уравнение не имеет корней, остаётся единственная серия:
Второе уравнение не имеет корней, остаётся единственная серия:

| |
Возможное решение второго уравнения:
Проверка необходима, так как тангенса половинного угла нет в изначальном уравнении. В ходе проверки выясняется, что серия  будет корнем, поэтому мы включаем её в ответ.
Далее пользуемся формулами универсальной тригонометрической подстановки: будет корнем, поэтому мы включаем её в ответ.
Далее пользуемся формулами универсальной тригонометрической подстановки:
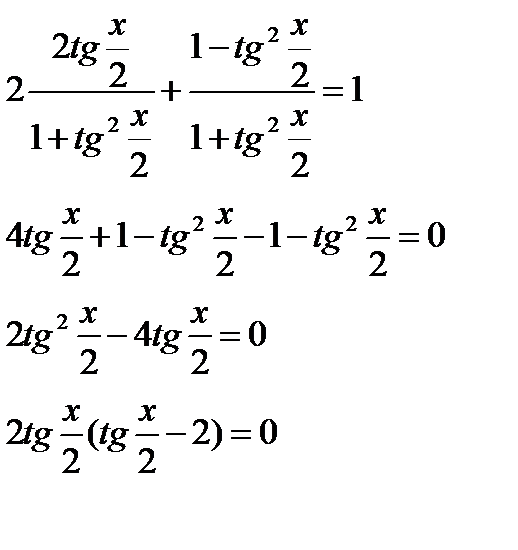 Критерий равенства произведения 0, проговаривается
Критерий равенства произведения 0, проговаривается
 или или  Отсюда получаем серии корней:
Отсюда получаем серии корней:
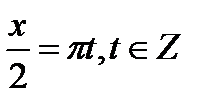 или или  Итого ответ:
Итого ответ:

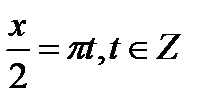
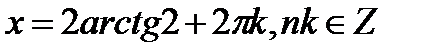
|
Проверка знаний
Цель данного этапа получить обратную связь от учащихся. Увидеть насколько они поняли суть метода и насколько они научились его применять, чтобы понять какой будет следующий урок.
Ученикам предлагается самостоятельно решить уравнение, к доске для самостоятельного решения вызывается ученик. Возможное решение:
Проверка не требуется.
 Критерий равенства произведения 0, проговаривается. Отсюда:
Критерий равенства произведения 0, проговаривается. Отсюда:
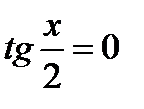 или или  Решая второе уравнение с помощью дискриминанта, и используя нечетность тангенса, получаем следующие серии корней:
Решая второе уравнение с помощью дискриминанта, и используя нечетность тангенса, получаем следующие серии корней:
 Отсюда:
Отсюда:
 После того как ученики решают уравнение, учитель выясняет сколько учеников успешно справилось с решением и если ребята ошиблись, то где они допустили ошибку.
После того как ученики решают уравнение, учитель выясняет сколько учеников успешно справилось с решением и если ребята ошиблись, то где они допустили ошибку.
|
Итог урока
Учитель поздравляет учеников с тем, что они узнали ещё один способ решения тригонометрических уравнений, ещё раз повторяет алгоритм его применения. После чего предлагает учащимся попытаться решить следующее уравнение различными способами:
| Должны быть обязательно названы следующие методы: 1) Универсальной тригонометрической подстановки; 2) Вспомогательного угла; 3) Применение формул приведения, с целью использование формул суммы (то есть разложение на множители); 4) Ограничение области значения синуса и косинуса; Возможно, также рассмотреть возведение в квадрат. |

Содержание
ВВЕДЕНИЕ.. 3
Глава 1 Тригонометрические уравнения в школьном курсе математики. 4
1.1 Роль и место тригонометрических уравнений в школьном курсе математики 4
1.2 Обзор методической литературы.. 6
Глава 2 Методические и технологические аспекты подготовки школьников к сдаче ЕГЭ по математике по теме «Тригонометрические уравнения». 9
2.1 Виды простейших тригонометрических уравнений и методы их решения 9
2.2 Общие методы решения тригонометрических уравнений. 12
Глава 3 Основные типы учебных задач темы и приемы их решения. 32
3.1 Базовые задачи: 32
3.2 Задачи для самостоятельного решения. 37
Глава 4 Характерные затруднения учащихся при решении тригонометрических уравнений и пути их преодоления. 39
Заключение. 46
Литература. 47
Приложение 1. 49
ВВЕДЕНИЕ
Тригонометрия является одним из наиболее молодых отделов элементарной математики. На первоначальных стадиях своего развития тригонометрия служила средством решения вычислительных геометрических задач. Ее содержанием считалось вычисление элементов простейших геометрических фигур, то есть треугольников. Но в современной тригонометрии самостоятельное значение имеет изучение тригонометрических функций и их свойств. Этот период развития тригонометрии был подготовлен всем ходом развития механики колебательных движений, физики звуковых, световых и электромагнитных волн. Исторически сложилось, что тригонометрическим уравнениям и неравенствам уделялось особое место в школьном курсе. Еще греки на заре человечества, считали тригонометрию важнейшей из наук. Поэтому и мы, не оспаривая древних греков, будем считать тригонометрию одним из важнейших разделов школьного курса, да и всей математической науки в целом.
Решение тригонометрических уравнений создаёт предпосылки для систематизации знаний учащихся, связанных со всем учебным материалом по тригонометрии (например, свойства тригонометрических функций, приёмы преобразования тригонометрических выражений и т.д.) и даёт возможность установить действенные связи с изученным материалом по алгебре (уравнения, равносильность уравнений, неравенства, тождественные преобразования алгебраических выражений и т.д.).
Иначе говоря, рассмотрение приёмов решения тригонометрических уравнений предполагает своего рода перенос этих умений на новое содержание.
Перед учителем стоит задача – формировать у учащихся умения решать уравнения каждого вида, развивая тем самым общие тригонометрические представления.
В процессе разработки методических и технологических аспектов подготовки учащихся к ЕГЭ по теме «Тригонометрические уравнения» необходимо было решить следующие задачи:
1. Провести анализ психолого-педагогической, учебной и методической литературы по проблеме исследования.
2. Выявить роль тригонометрических уравнений в обучении математики.
3. Выделить основы формирования умений необходимых для решения тригонометрических уравнений.
4. Классифицировать методы решения тригонометрических уравнений.
5. Разработать методику формирования умений и навыков решать тригонометрические уравнения.
6. Провести экспериментальное исследование разработанной методики; выделить типичные ошибки учащихся и их причины.
7. Сделать подборку заданий для подготовки учащихся к ЕГЭ.
Глава 1 Тригонометрические уравнения в школьном курсе математики
|
| Поделиться: |

 , где
, где  тригонометрическая функция часто называются сводящимися к квадратным и решаются методом подстановки вместо тригонометрической функции данного аргумента некоторого параметра t с учётом допустимых значений t в зависимости от области значения функции.
тригонометрическая функция часто называются сводящимися к квадратным и решаются методом подстановки вместо тригонометрической функции данного аргумента некоторого параметра t с учётом допустимых значений t в зависимости от области значения функции.
 тогда уравнение примет вид:
тогда уравнение примет вид:
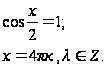
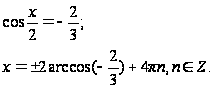
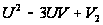 ; третьей степени:
; третьей степени:  и т.д., сформировав понятия выражения, однородного относительно переменных U и V.
и т.д., сформировав понятия выражения, однородного относительно переменных U и V. .
.
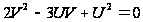 ;
;
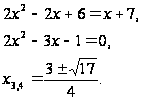
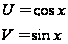 .
. .
.
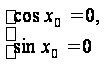
 .
.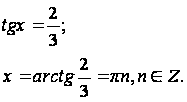
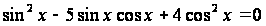 .
. .
.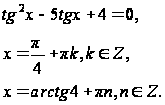

 или
или 

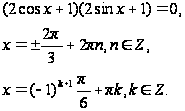




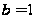 ;
;
 , т.к. это решение системы
, т.к. это решение системы 




 , т.к. это решение системы
, т.к. это решение системы 

 .
. где
где 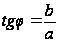 .
.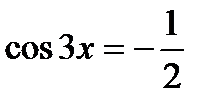
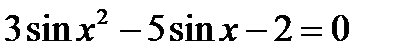
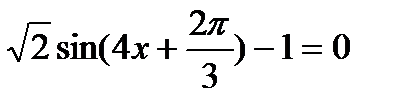
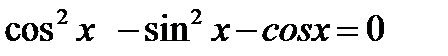
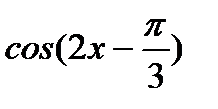 найдите координаты общих точек ее графика с прямой у=-1
найдите координаты общих точек ее графика с прямой у=-1
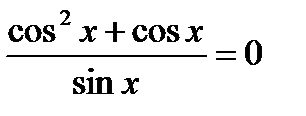
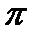 )
)
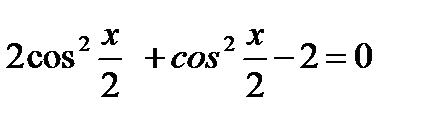
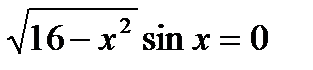
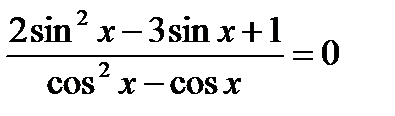
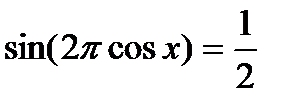
 имеет решение. Найдите все его решения.
имеет решение. Найдите все его решения.



