
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольная работа по математике ( 2 курс)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ВАРИАНТ 1. 1. Найти пределы: а) 2. Используя определение производной, доказать равенство: (2х2+1)/ =4х 3. Найти производные: а) у=(1+sin x)х2 б) у=(1-2х3 +3х5)5 в) у= 4. Построить графики функций: а) у= 5. Найти наибольшее и наименьшее значения функции у=х2-6х+13 при хЄ[1,6]. 6. Составить уравнение касательной к графику функции у=х2-7х+10 в точке х=4. 7. Тело движется прямолинейно по закону s=2t3 + t2 - 4. Найти: а) среднюю скорость движения тела за промежуток времени от t1 =4 до t2 =6; б) найти значение скорости и ускорения в момент t =4.
ВАРИАНТ 2. 1. Найти пределы: а) 2. Используя определение производной, доказать равенство: (5х2 -3)/ =10х 3. Найти производные: а) у=х3(1-4х) б) у= 4. Построить графики функций: а) у= 5. Найти наибольшее и наименьшее значения функции у=8-0,5х2 при хЄ[-2,2]. 6. Составить уравнение касательной к графику функции у=х2-5х+6 в точке х=4. 7. Тело движется прямолинейно по закону s=4t2 + t -1. Найти: а) среднюю скорость движения тела за промежуток времени от t1 =2 до t2 =7; б) найти значение скорости и ускорения в момент t =5. ВАРИАНТ 3. 1. Найти пределы: а) 2. Используя определение производной, доказать равенство: (8-3х2)/ = -6х 3. Найти производные: а) у=2х5(4х3 +6) б) у= 4. Построить графики функций: а) у=2х3 -3х2 -12х-1 б) у= 5. Найти наибольшее и наименьшее значения функции у=6х2-х3 при хЄ[-1,6]. 6. Составить уравнение касательной к графику функции у=х2-3х-4 в точке х=3. 7. Тело движется прямолинейно по закону s=2t3+t2 -4. Найти: а) среднюю скорость движения тела за промежуток времени от t1 =1 до t2 =4; б) найти значение скорости и ускорения в момент t =4.
ВАРИАНТ 4. 1. Найти пределы: а) 2. Используя определение производной, доказать равенство: (4х2-3)/ = 8х 3. Найти производные: а) у= 4. Построить графики функций: а) у=2х3 +3х2 -12х-10 б) у= 5. Найти наибольшее и наименьшее значения функции у=х3-3х2 -9х+35 при хЄ[-4,4]. 6. Составить уравнение касательной к графику функции у=х2+7х+12 в точке х=1. 7. Тело движется прямолинейно по закону s=t3+5t2+4. Найти: а) среднюю скорость движения тела за промежуток времени от t1 =1 до t2 =5; б) найти значение скорости и ускорения в момент t =2.
ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ ПО МАТЕМАТИКЕ 1. РЕШЕНИЕ ПРОСТЕЙШИХ УРАВНЕНИЙ: а) 2х2-х-1=0; б) 3х2+5х=0; в) 4х2-9=0;
2. РЕШЕНИЕ ПРОСТЕЙШИХ НЕРАВЕНСТВ:
а) 2х2-х-1≥0; б) 5х2-3х=0; в) 9х2-4<0; г) х2≥7;
3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ: а)
4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ: а)
5. РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ: а) 5х=1; б) 4х=8; в) 72х-6▪7х+5=0; г) 5х+1+5х=750;
6. РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ НЕРАВЕНСТВ: а)
7. РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ: а)
8. РЕШЕНИЕ ЛОГПРИФМИЧЕСКИХ НЕРАВЕНСТВ: а)
9. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ: а)
10. РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ МЕТОДОМ КРАМЕРА: а) 11. НАЙТИ ПРЕДЕЛЫ: а)
12. НАЙТИ ПРОИЗВОДНЫЕ: а) у=3х5+6х-11; б) у=х3(5х8-4cosx); в) у=
13. ПОСТРОИТЬ ГРАФИКИ ФУНКЦИЙ: а) у=3х; б) у=(2/5)х; в) у=
14. ПОСТРОИТЬ ГРАФИКИ ФУНКЦИЙ, ИСПОЛЬЗУЯ ПРОИЗВОДНУЮ: а) у=2х3-3х2-12х-1; б) у= 15. НАЙТИ СКОРОСТЬ И УСКОРЕНИЕ, ЕСЛИ ДВИЖЕНИЕ ТОЧКИ ЗАДАНО УРАВНЕНИЕМ: s(t) = t3+5t2+4;
16. УПРОСТИТЬ ВЫРАЖЕНИЯ: а) sin2x+cos2x-1; б) sin4x-cos4x+cos2x; в) cos2x+sin2x; г) (cosx - sinx)2+sin2x; д) 5 - е) ж) з)
КОНТРОЛЬНАЯ РАБОТА. ВАРИАНТ 1 1. Вычислить пределы: а) 2. Решить уравнения: а) 3х-5 = 81; б) 3. Решить систему линейных уравнений методом Крамера: 4. Исследовать функцию и построить её график: у = 2х3-3х2-12х+1; 5. Найти наименьший положительный корень уравнения: cosx + cos2x = 1/2 – sin2x; 6. Решить неравенство: (х-1) 7. Решить уравнение:
ВАРИАНТ 2 1. Вычислить пределы: а) 2. Решить уравнения: а) 4х-3 = 64; б) 3. Решить систему линейных уравнений методом Крамера: 4. Исследовать функцию и построить её график: у = 2х3-9х2+12х-15; 5. Найти наибольший отрицательный корень уравнения: 2sinx + sin2x = - cos2x; 6. Решить неравенство: 7. Решить уравнение:
Итоговый тест по математике В номерах А1 – А10 указать правильный вариант ответа: А1. Упростить выражение: (5у0,7)3▪у-0,9. а) 125у3 б) 125у1,2 в) 15у1,2 г) 1252,8 А2. Найти длину вектора а)4 б) 1 в) 2 г) 1/2 А3. Найти значение выражения: а) -4 б) -2 в) -1 г) -1 + А4. Вычислить определитель: а) 44 б) -68 в) -44 г) 68 А5. Найти область определения функции: у = а) (- А6. Найти координаты вектора, проходящего через точки А(2,-1) и В(-3,8): а) (-5,9) б) (-1,7) в) (5,-7) г) (-5,7) А7. Решить уравнение: (0,7)4х = 0,49: а) 1/4 б) 1 в) 2 г) 1/2 А8. Решить неравенство:
а) (0,3) б) (-3,+ А9. Найти объём пирамиды, если площадь её основания равна 3√2 м2, а высота √3 м: а) 3√6м3 б) √6м3 в) 18м3 г) 18√3м3 А10. Найти предел а) 0 б) 4 в) 8 г)
В номерах В1 – В3 записать правильный ответ: В1. Мальчик толкнул футбольный мяч, который после этого стал двигаться по закону S(t) = -0,5t2+6t, где S – пройденное мячом расстояние, измеряемое в метрах, а t – прошедшее после начала движения время, измеряемое в секундах. Через сколько секунд после начала движения мяч остановится? Ответ: _____________ В2. Найти целый корень уравнения 1 – sinx = cos2x. Ответ:______________ В3. Найти площадь фигуры, ограниченной линиями: у=2х2+1, у=1, х=3, х=6. Ответ:______________
Записать подробное решение номера С1 с обратной стороны листа. с1. При каких х выполняется неравенство
Задания для контрольных работ
ВАРИАНТ 1
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1) 2) ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 При каких размерах коробка (без крышки), изготовленная из квадратного листа картона, со стороной a, имеет наибольшую вместимость? ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: 1) y=6x-x2 и y=0. ВАРИАНТ 2
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1) 2)
ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Среди всех прямоугольников, имеющих данный периметр 2a, найти тот, площадь которого наибольшая. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2. Вычислить площади фигур, ограниченных линиями: y=x2+4x и x-y+4=0. ВАРИАНТ 3
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1. Исследовать на экстремум: 1) ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Кусок проволоки данной длины l согнуть в виде прямоугольника так, чтобы площадь последнего была наибольшей. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: 1) y=x3 и y=x. ВАРИАНТ 4
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1) ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3
Число 50 записать в виде суммы двух чисел, сумма кубов которых наименьшая. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: y=x3 и y=2x. ВАРИАНТ 5
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1)
ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Записать число 625 в виде произведения двух положительных чисел так, чтобы сумма их квадратов была наименьшая. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: y=2
ВАРИАНТ 6
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1)
ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Из всех прямоугольников, площадь которых равна 9 см2, найти прямоугольник с наименьшим периметром. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: y=2
ВАРИАНТ 7
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1) ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Из всех прямоугольных параллелепипедов, у которых в основании лежит квадрат и площадь полной поверхности равна 600 см2, найти параллелепипед наибольшего объема. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: 1) 3y=x2 и y= 3 ВАРИАНТ 8
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1)
ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Из всех прямоугольников с периметром P найти прямоугольник с наименьшей диагональю. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: 1) y=x2-3x и y=4-3x
ВАРИАНТ 9
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1) ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Из всех равнобедренных треугольников с периметром P найти треугольник с наибольшей площадью. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: y=2x-x2 и y=x.
ВАРИАНТ 10
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1) ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Из всех прямоугольных треугольников, у которых сумма одного катета и гипотенузы равна l, найти треугольник с наибольшей площадью. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1) ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: 1) Вопросы к зачёту.
1. Практические приемы вычислений с приближенными данными. 2. Линейные уравнения с одной переменной 3. Линейные неравенства с одной переменной 4. Квадратные уравнения. 5. Квадратные неравенства 6. Иррациональные уравнения 7. Иррациональные неравенства 8. Решение систем линейных уравнений 9. Решение систем линейных уравнений с двумя и тремя неизвестными с помощью определителей второго и третьего порядка 10. Предел числовой последовательности 11. Простейшие преобразования графиков функций. 12. Основные свойства предела. 13. Первый и второй замечательные пределы. 14. Преобразование и вычисление значений показательных выражений.
15. Преобразование и вычисление значений логарифмических выражений. 16. Построение графиков показательных функций 17. Построение графиков логарифмических функций 18. Построение графиков степенных функций 19. Показательные уравнения 20. Логарифмические уравнения 21. Показательные неравенства 22. Логарифмические неравенства
Вопросы к экзамену.
1. Синус, косинус, тангенс, котангенс числа. 2. Соотношения между тригонометрическими функциями одного аргумента 3.. Вычисление значений и тождественные преобразования тригонометрических выражений 4. Свойства и графики тригонометрических функций 5. Простейшие тригонометрические уравнения 6. Производная, ее геометрический и механический смысл 7. Производные суммы, произведения и частного двух функций. 8. Признаки возрастания и убывания функции 9. Применение производной к построению графиков функции 10. Наибольшее и наименьшее значения функции на промежутке. 11. Неопределенный интеграл и его свойства 12. Определенный интеграл и его геометрический смысл 13. Способы вычисления определенного интеграла. 14. Вычисление площадей плоских фигур с помощью определенного интеграла 15. Векторы на плоскости и в пространстве. 16. Формулы для вычисления длины вектора, угла между векторами, расстояния между двумя точками 17. Аксиомы стереометрии и простейшие следствия из них. 18. Многогранники. Призма. Параллелепипед и его свойства пирамида. 19. Тело вращения. Цилиндр и конус 20. Объемы и площади поверхностей геометрических тел
Список рекомендуемой литературы.
Основная литература: 1. Пехлецкий И.Д. Математика: учебник – М.: ИЦ «Академия», 2002 Гриф 2. Колмогоров А.Н. Алгебра и начала математического анализа 10-11 кл.: учебник – М.: «Просвещение», 2009 Гриф 3. Дадаян А.А. Математика: учебник – М.: «Форум», 2010 Гриф
Дополнительная литература:
1. Пехлецкий И.Д. Математика: Учебник для средних специальных учебных заведений. – М.: Академия, 2003. 2. Богомолов Н.В. Практические занятия по математике: Учебное пособие, 5-е изд. – М.: Высшая школа, 2002.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 2383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.244.136 (0.012 с.) |


 б)
б) 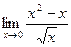 в)
в) 

 б) у=
б) у= 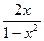
 б)
б)  в)
в) 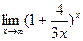
 в) у=
в) у= 
 б) у=
б) у= 
 б)
б) 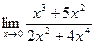 в)
в) 
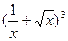 в) у=
в) у= 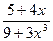

 б)
б)  в)
в) 
 б) у=
б) у=  в) у=
в) у= 

 ; б)
; б)  ;
; ; б)
; б)  ; в)
; в)  ;
; ; б) (1/3)х<81; в) 3х≥4;
; б) (1/3)х<81; в) 3х≥4; б) lg(x-3) + lg(x-2) = 1 – lg5;
б) lg(x-3) + lg(x-2) = 1 – lg5; ; б)
; б)  ;
; sinx = 2; б) - √2cosx = 1; в) 4cos2x+sinx-1=0;
sinx = 2; б) - √2cosx = 1; в) 4cos2x+sinx-1=0; б)
б) 
 ; б)
; б)  ; в)
; в)  ;
; ; г) у=5(2cos4x-1)3;
; г) у=5(2cos4x-1)3; ; г) у=
; г) у=  ; д) у=sinx; е) у=cosx
; д) у=sinx; е) у=cosx ;
; ;
; ;
; ;
;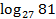 ;
;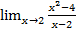 ; б)
; б)  ;
; ;
;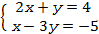
 .
. .
. ; б)
; б)  ;
;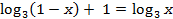 ;
;


 , проходящего через точку А(1,-2):
, проходящего через точку А(1,-2): +
+ 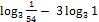
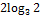
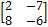 :
: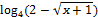
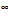 ;2) б) (-1,3) в) [-1,3) г) (-1,1)
;2) б) (-1,3) в) [-1,3) г) (-1,1)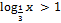 :
: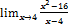 :
: .
.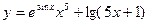
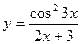
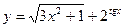




 ,
,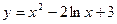 .
. на отрезке
на отрезке  .
.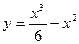 .
. .
. .
.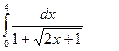 2)
2)  .
.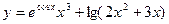
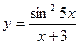
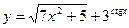


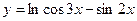
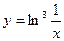
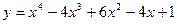 ,
,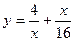 .
. на отрезке
на отрезке 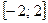 .
.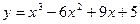 .
.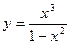 .
.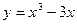 .
.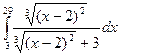 2)
2) 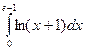 .
.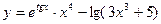
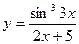
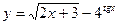
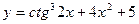
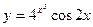
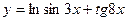

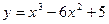 , 2)
, 2)  .
.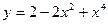 на отрезке
на отрезке  .
.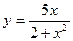 .
. .
.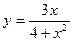 .
.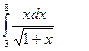 2)
2)  .
.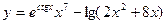
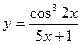

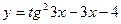
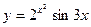
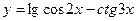
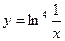
 , 2)
, 2)  .
.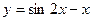 на отрезке
на отрезке  .
.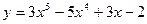 .
.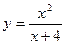
 .
.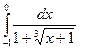 2)
2)  .
.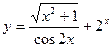
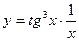
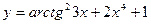
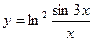
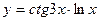
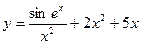

 , 2)
, 2)  .
.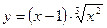 на отрезке
на отрезке 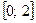 .
. .
.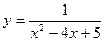 .
.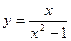 .
. 2)
2)  .
.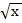 и y=x.
и y=x.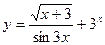
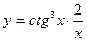
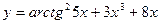
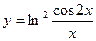
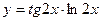

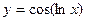
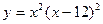 , 2)
, 2) 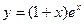 .
.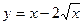 на отрезке
на отрезке  .
.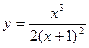 .
. 2)
2)  .
.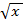 и
и  .
.


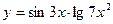

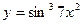
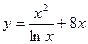
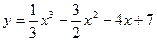 , 2)
, 2)  .
. на отрезке
на отрезке 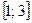 .
. .
.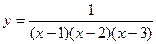 .
.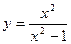 .
.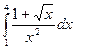 2)
2)  .
. .
.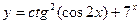
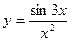
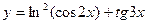

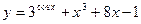
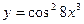
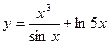
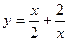 , 2)
, 2)  .
.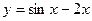 на отрезке
на отрезке  .
. .
.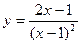 .
.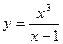 .
.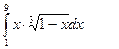 2)
2) 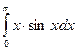 .
.
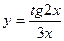


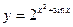
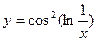

 , 2)
, 2)  .
.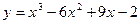 на отрезке
на отрезке 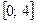 .
.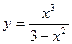 .
. 2)
2) 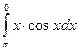 .
.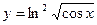
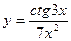

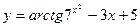
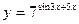
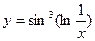
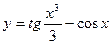
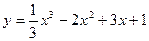 , 2)
, 2)  .
.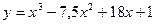 на отрезке
на отрезке  .
.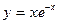 .
.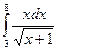 2)
2) 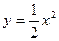 и y=4-x.
и y=4-x.


